Лаб раб. 3 лб. Конденсатор и катушка индуктивности в цепи синусоидального тока
 Скачать 279.66 Kb. Скачать 279.66 Kb.
|
|
РАБОТА 3 КОНДЕНСАТОР И КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА Цель работы. Научиться определять параметры конденсатора и катушки индуктивности с помощью амперметра, вольтметра и фазометра, строить векторные диаграммы, а также проверить выполнение законов Кирхгофа в цепи синусоидального тока. Пояснения к работе Реальный конденсатор в отличие от идеального обладает некоторыми тепловыми потерями энергии из-за несовершенства изоляции (проводимость g). В расчетах электрических цепей конденсатор представляют обычно параллельной схемой замещения. На рис.3.1 схема замещения конденсатора обведена пунктиром. Параметры g и С можно экспериментально определить по показаниям амперметра I, вольтметра U и фазометра следующим образом. Сначала найти по закону Ома полную проводимость конденсатора 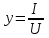 , потом активную , потом активную 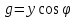 и емкостную и емкостную 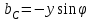 проводимости, а затем по известной угловой частоте синусоидального напряжения сети ( = 314 рад/с) подсчитать емкость проводимости, а затем по известной угловой частоте синусоидального напряжения сети ( = 314 рад/с) подсчитать емкость 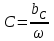 . .Напряжение на конденсаторе отстает по фазе от тока, с учетом потерь в изоляции угол сдвига фаз: 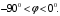 Угол потерь, характеризующий несовершенную изоляцию конденсатора, равен 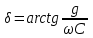 ; очевидно, ; очевидно, 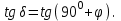 Реальная катушка индуктивности также обладает тепловыми потерями в отличие от идеальной катушки. Эквивалентную схему замещения такой катушки обычно представляют в виде последовательного соединения элементов R и L. На рис.3.2 схема замещения катушки индуктивности обведена пунктиром. Эти параметры можно экспериментально определить по показаниям вышеупомянутых приборов, воспользовавшись формулами: 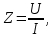 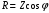 , , 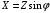 , , 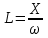 . .Напряжение в катушке индуктивности опережает ток по фазе, с учетом потерь в сопротивлении R угол сдвига фаз: 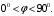 Тангенсом этого угла оценивается добротность катушки: 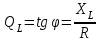 . .Подготовка к работе Какие физические явления отражают в схеме замещения конденсатора элементы g, C, а в схеме замещения катушки индуктивности – элементы R, L? Что такое активная, емкостная, индуктивная, реактивная, полная проводимости? Как они связаны между собой? Что такое активное, емкостное, индуктивное, реактивное, полное сопротивления? Как они связаны между собой? В каких пределах может изменяться угол сдвига фаз напряжения и тока на входе пассивного двухполюсника? Записать уравнение по первому закону Кирхгофа для схемы рис. 3.1 и уравнение по второму закону Кирхгофа для схемы рис. 3.2 как для мгновенных, так и для комплексных значений токов и напряжений. 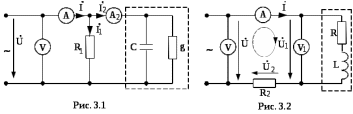 Здесь 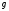 - проводимость, отражающее потери в изоляции конденсатора. - проводимость, отражающее потери в изоляции конденсатора.R – активное сопротивление проводника катушки индуктивности. 3а. ИССЛЕДОВАНИЕ АКТИВНО-ЕМКОСТНОЙ ЦЕПИ Схема электрической цепи Собрать цепь по схеме рис. 3.1 с параметрами согласно варианту, указанному преподавателем (табл. 3.1). Таблица 3.1
Установить необходимые частоту и напряжение источника и записать показания приборов и параметры схемы в табл. 3.2 (величину сопротивления R1 уточнить измерением омметром). Таблица 3.2
Ток 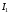 определяется по закону Ома: определяется по закону Ома: 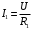 . .Выбрать масштабы векторов напряжения и токов. Принять начальную фазу входного напряжения равной нулю: 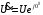 . Ток . Ток 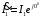 , протекающий через резистор R1 совпадает по фазе с входным напряжением , протекающий через резистор R1 совпадает по фазе с входным напряжением 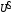 . . Построить вектора 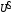 и и 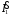 на комплексной плоскости вдоль оси вещественных чисел. Дополнить остальными двумя токами лучевую диаграмму. Векторы на комплексной плоскости вдоль оси вещественных чисел. Дополнить остальными двумя токами лучевую диаграмму. Векторы 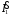 и и 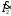 образуют при сложении параллелограмм, диагональю которого является ток образуют при сложении параллелограмм, диагональю которого является ток 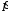 (все векторы токов строятся в одном масштабе mI ). Вершину этого параллелограмма можно найти с помощью засечек циркулем. Измерить транспортиром углы (все векторы токов строятся в одном масштабе mI ). Вершину этого параллелограмма можно найти с помощью засечек циркулем. Измерить транспортиром углы 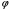 и и 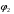 , полученные измерения внести в табл. 3.2. Пример векторной диаграммы показан на рис. 3.3. , полученные измерения внести в табл. 3.2. Пример векторной диаграммы показан на рис. 3.3.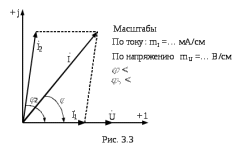 Подсчитать параметры конденсатора g и C. Результаты этих вычислений внести в табл. 3.2, причем 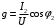 , , 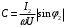 . .Проверить в комплексной форме выполнение первого закона Кирхгофа: 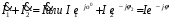 , полученное значение модуля входного тока , полученное значение модуля входного тока 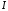 занести в табл.3.2 и сравнить со значением занести в табл.3.2 и сравнить со значением 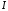 , полученном в эксперименте. , полученном в эксперименте. 3а. ИССЛЕДОВАНИЕ АКТИВНО-ИНДУКТИВНОЙ ЦЕПИ Схема электрической цепи Собрать электрическую цепь по схеме, показанной на рис. 3.2 с параметрами, соответствующими варианту из табл. 3.1, который указан преподавателем. Установить требуемые значения U и f . Параметры цепи и показания приборов записать в табл. 3.3 (величину сопротивления R2 уточнить измерением омметром). Таблица 3.3
Напряжение 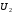 определяется по закону Ома: определяется по закону Ома: 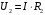 . .Выбрать масштабы векторов напряжения и токов. Принять начальную фазу входного тока равной нулю: 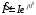 . Напряжение на резисторе R2 совпадает по фазе с током . Напряжение на резисторе R2 совпадает по фазе с током 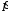 , поэтому , поэтому 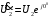 . .Построить вектора 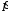 и и 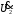 на комплексной плоскости вдоль оси вещественных чисел. Дополнить топографическую диаграмму напряжений векторами на комплексной плоскости вдоль оси вещественных чисел. Дополнить топографическую диаграмму напряжений векторами 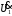 и и 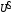 (все векторы напряжений строятся в одном масштабе mU ). Векторы напряжений образуют треугольник, одна из вершин которого лежит в начале координат, а другую можно найти с помощью засечек, сделанных циркулем. Пример векторной диаграммы показан на рис. 3.4. Измерить транспортиром углы (все векторы напряжений строятся в одном масштабе mU ). Векторы напряжений образуют треугольник, одна из вершин которого лежит в начале координат, а другую можно найти с помощью засечек, сделанных циркулем. Пример векторной диаграммы показан на рис. 3.4. Измерить транспортиром углы 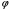 и и 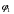 , полученные измерения внести в табл. 3.3. , полученные измерения внести в табл. 3.3. 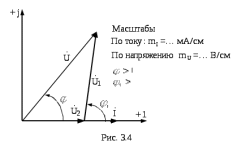 Вычислить параметры катушки RL, L. Найденные величины сравнить со значениями, установленными в схеме. Результаты вычислений внести в табл. 3.3, причем 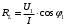 , , 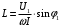 . .Проверить в комплексной форме выполнение второго закона Кирхгофа: 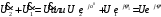 , полученное значение модуля входного напряжения , полученное значение модуля входного напряжения 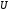 занести в табл.3.3 и сравнить со значением занести в табл.3.3 и сравнить со значением 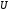 , полученном в эксперименте. , полученном в эксперименте. Сделать общие выводы по работе. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
