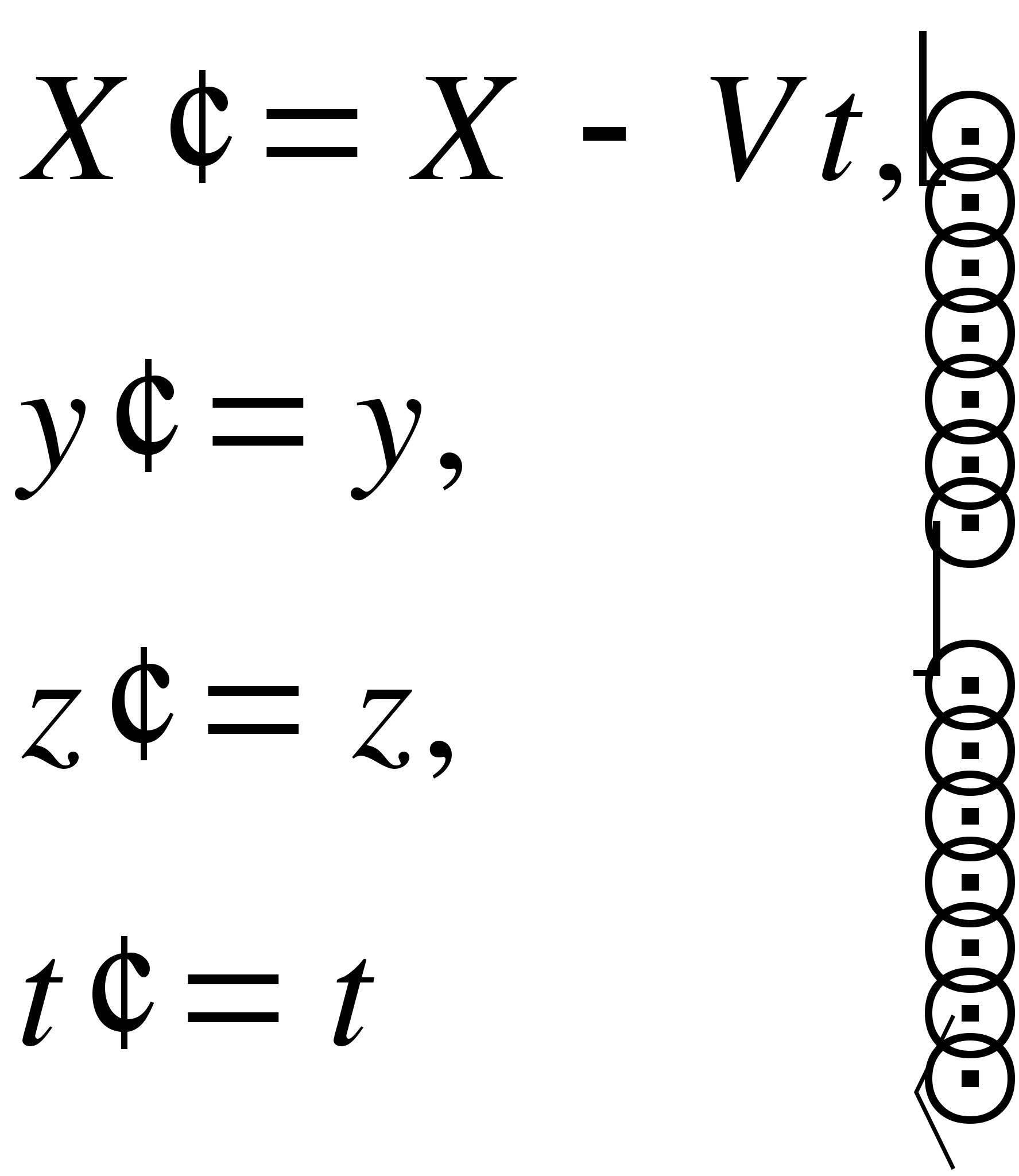Конспект лекций по физике Лекция 3 Лекция динамика материальной точки поступательного движения твердого тела

• Название: Конспект лекций по физике Лекция 3 Лекция динамика материальной точки поступательного движения твердого тела
• Дата: 29.01.2018
• Размер: 303.5 Kb.
• Имя файла: 03_DINAMIKA_MATERIAL_NOJ_TOChKI.doc
• Тип: Конспект лекций; #35436

Федун В.И. Конспект лекций по физике Лекция 3

Лекция 3.

2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ (ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА).

Если на материальную точку действует одновременно несколько сил, то каждая из них сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. 27

Динамика является основным разделом механики, и в ее основе лежат три закона Ньютона, сформулированные им в 1687 году. Их рассматривают как систему взаимосвязанных законов и опытной проверке подвергают не каждый отдельный закон, а всю систему в целом.
2.1.Первый закон Ньютона.

ЗАКОН !

I закон Ньютона (Закон инерции): Существуют такие системы отсчета, в которых всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставят ее изменить это состояние, и эти системы отсчета называются инерциальными.

2.1.1. Инерциальные и неинерциальные системы отсчета.
Утверждение, что существуют инерциальные системы отсчета и составляет сущность первого закона Ньютона.

Инерциальной системой отсчета называется такая система, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно (т.е. такой системой, в которой выполняется первый закон Ньютона).

Неинерциальной системой отсчета называется система, движущаяся относительно инерциальной системы либо поступательно с ускорением либо вращаясь.

Опытным путем установлено, что инерциальной можно считать гелиоцентрическую (звездную) систему отсчета, у которой начало координат находится в центре Солнца, а оси проведены в направлении определенных звезд.

Система координат, связанная с Землей, строго говоря неинерциальная. Однако, эффекты, обусловленные ее неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца), при решении многих задач и проведении многих экспериментов пренебрежимо малы, и во многих случаях систему связанную с Землей можно считать инерциальной.
2.1.2. Инертность тел. Масса.
Наличие у тел инертности, т.е. свойства сохранять свою скорость, как по величине так и по направлению - второе утверждение, содержащееся в первом законе Ньютона.

Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью.

Из опыта известно, что при одинаковых взаимодействиях различные тела приобретают различные ускорения, следовательно, ускорение зависит не только от величины воздействия, но и от свойств самого тела, т.е. от его массы.

Масса тела – это физическая величина, являющаяся одной из характеристик материи, определяющая ее инерциальные (инертная масса) и гравитационные (гравитационная масса) свойства.

В настоящее время принято считать, что инерционная масса равна гравитационной с точностью до 10^–12 их значений.
Свойства массы в классической механике:

Масса - величина аддитивная, т.е. масса составного тела равна сумме масс его частей.

Масса замкнутой системы тел - величина постоянная при любых процессах, происходящих в этой системе (закон сохранения массы).

Масса (в классической механике) не зависит от состояния движения, от собственно кинематических параметров (координаты, скорости, ускорения

Единица массы - 1кг.
2.1.3. Сила, Импульс силы.
Чтобы описывать воздействие, упоминаемое в I законе Ньютона, вводят понятие силы. В каждый момент времени сила характеризуется численным значением, направлением в пространстве и точкой приложения.

Сила есть векторная величина, являющаяся мерой воздействия на тело других тел или полей, в результате которого тело приобретает ускорение или/и деформируется.

Единица измерения силы – 1 Ньютон (Н).

Элементарным импульсом силы называется векторная величина численно равная произведению силы на элементарный промежуток времени ее действияdt:

(2.1)

Импульс силы за конечный промежуток времени от t₁ до t₂ равен определенному интегралу:

(2.2)

2.2. Второй закон Ньютона.
2.2.1. Импульс материальной точки.
Импульсом (или количеством движения) материальной точки (тела) называется векторная величина, численно равная произведению массы материальной точки (тела) на ее скорость и имеющая направление скорости:

(2.3)

Единица измерения - 1 кг_*м/с - « один килограмм-метр на секунду ».
2.2.2. Формулировка второго закона Ньютона –основного закона динамики.
Формулировка Ньютона (в переводе А.Н. Крылова):

“ Изменение количества движения пропорционально движущей силе и происходит по направлению той прямой, по которой эта сила действует.”

Воспользуемся современным языком:

ЗАКОН !

“ Производная от импульса (количества движения) по времени равна по величине действующей силе и совпадает с ней по направлению ”: (2.4) “ Скорость изменения импульса материальной точки равна действующей на нее силе ”.

II закон Ньютона – это основной закон динамики поступательного движения твердого тела. Он отвечает на вопрос, как изменяется механическое движение материальной точки или тела под воздействием приложенных к ней сил.

Уравнение (2.4) называется уравнением движения (в дифференциальной форме).

II закон Ньютона справедлив только для инерциальных систем отсчета!
2.2.3. Принцип независимости действия сил.

Из II закона Ньютона следует принцип независимости сил:

Если на материальную точку действует одновременно несколько сил, то каждая из них сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было.

Если на точку (тело) действует несколько сил , то:

(2.5)

где - главный вектор сил.

Главный вектор сил есть геометрическая сумма (находится по правилу параллелограмма) всех векторов сил, приложенных к телу.

Следствие из II закона Ньютона: Учитывая, что в классической механике m = const, мы можем и (2.4) вынести m из-под знака дифференциала. Тогда



Это только математическое следствие, но не физическое. Поэтому, единица измерения силы - 1 Ньютон = 1 кг_*м/с² - сила, которая сообщает телу массой 1кг, ускорение равное 1 м/с² в направлении действия силы.


2.3. Третий закон Ньютона.

Механическое действие тел друг на друга проявляется в виде их взаимодействия.
2.3.1. Формулировка третьего закона Ньютона.

ЗАКОН !

“ Две взаимодействующие материальные точки действуют друг на друга с силами одной природы, которые численно равны и направлены в противоположные стороны вдоль прямой, соединяющие эти точки “.

Если - сила, действующая на i-тую материальную точку со стороны k-той материальной точки, а - сила, действующая на k-тую материальную точку со стороны i-той, то согласно третьему закону Ньютона:

(2.6)

Подчеркнем, что силы в третьем законе Ньютона:

• 
  приложены к разным материальным точкам;
  
• 
  в любой системе тел действуют парами;
  
• 
  имеют одну природу.
  
• 
  Сам третий закон применим только в рамках классической механики.
  

Силы и (приложенные к разным материальным точкам) могут взаимно уравновешиваться, только если эти точки принадлежат к одному телу.

Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системыматериальных точек. Это следует из того, что для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

Второй и третий законы Ньютона справедливы только для инерциальных систем отсчета!!!


2.3.2. Силы инерции.
В неинерциальных системах отсчета возникают силы инерции, которые вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как, если на какое-либо тело действует сила инерции, то нельзя указать со стороны какого тела она действует и, соответственно, не существует противодействующей силы. (Действие есть, а противодействия нет!).

2.4. Преобразования Галилея.
Галилей обратил внимание, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно, т.е. не привязав себя к другой инерциальной системе отсчета.

В основу классической механики положен принцип независимости пространства и времени. В качестве аксиом принимается абсолютность промежутков времени и длин:

1) промежуток времени между какими-либо двумя событиями одинаков во всех системах отсчёта; 2) размеры тела не зависят от скорости его движения относительно системы отсчёта. Преобразованиями Галилея называются преобразования коорди­нат и времени, применяемые в классической механике при переходе от одной инерциальной системы отсчёта (x, y, z, t) к другой (x’, y’,z’, t’), которая движется относительно системы прямолинейно и поступательно с постоянной скоростью .

Рисунок 2.1

Если сходные оси декартовых координат инерциальных систем отсчёта и проведены попарно параллельно друг другу, и если в начальный момент времени начала координат и совпадают друг с другом (рис. 2.1), то преобразования Галилея имеют вид:

и

(2.7)

или:

и

(2.8)

где: x,y,z и ,, - координаты точки М в системах отсчёта в момент времени t и в момент времени ; и - радиусы – векторы точки М в тех же системах отсчёта; ,, - проекции скорости системы на оси координат системы .

	Обычно оси координат проводят так, что система движется вдоль оси ОХ в положительном направлении (рис. 2.2.). В этом случае преобразования Галилея имеют более простой вид:
		(2.9)
Рисунок 2.2.

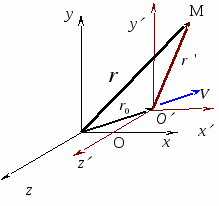
Из преобразований Галилея вытекает следующий закон преобразования скорости произвольной точки М (рис. 2.1.) при переходе от одной инерциальной системы к другой ,

(2.10)

где скорость точки М - в системе отсчета , и - в системе .

Соответственно преобразуются и проекции скорости на сходственные оси координат:

(2.11)

Ускорение точки М в системах отсчёта

(в ) и (в )

(2.12)

одинаковы.

(2.13)

Итак, ускорение материальной точки не зависит от выбора инерциальной системы отсчёта, т. е. инвариантно относительно преобразований Галилея.

Силы взаимодействия между материальными точками зависят только от их взаимного расположения и от скорости движения друг относительно друга.

Взаимное расположение каких-либо двух точек 2 и 1, характеризуется вектором, равным разности радиусов- векторов этих точек. В системе вектором , а в системе - вектором .

Согласно аксиоме 2 следует, что расстояния между точками 1 и 2 в системах одинаковы:

(2.14)

или:

(2.15)

Скорость движения точки 2 относительно точки 1 (относительная скорость) равна разности скоростей этих точек

В системе : В системе :

(2.16)

Из преобразований Галилея следует, что:

(2.17)

Итак, взаимное расположение и скорость относительного движения двух любых материальных точек не зависят от выбора инерциальной системы отсчёта, т. е. они инвариантны относительно преобразований Галилея. Соответственно инвариантны и силы, действующие на материальную точку:

(2.18)

Уравнения, выражающие законы Ньютона, инвариантны относительно преобразований Галилея, т. е. не изменяют свой вид при преобразовании координат и времени от одной инерциальной системы отсчёта к другой:

и - в системе и - в системе

(2.19)

где и - масса рассматриваемой материальной точки, одинаковая во всех системах отсчёта.

Т.о., в классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы механики одинаковы во всех инерциальных системах отсчёта.

Это значит, что в разных инерциальных системах отсчёта все механические процессы при одних и тех же условиях протекают одинаково.

Следовательно, с помощью любых механических экспериментов, проведённых в замкнутой системе тел, нельзя установить, покоится эта система или движется равномерно и прямолинейно (относительно какой-либо инерциальной системы отсчёта).

Механический принцип относительности означает, что в классической механике все инерциальные системы отсчёта совершенно равноправны.

Записанные соотношения справедливы в случае классической механики, т.е. u,  << c.

Для скоростей, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.
Вопросы для самоконтроля.

1. 
   Что изучается в разделе "Динамика"?
   
2. 
   Сформулируйте первый закон Ньютона.
   
3. 
   Какие системы отсчета называются инерциальными?
   
4. 
   Что такое инертность тел? Что такое масса? Единицы измерения массы. Как измеряется масса?
   
5. 
   Что такое сила и как она измеряется? Единицы измерения силы.
   
6. 
   Второй закон Ньютона. Импульс.
   
7. 
   В чем заключается принцип независимости действия сил?
   
8. 
   Сформулируйте третий закон Ньютона.
   
9. 
   Есть ли границы применимости механики Ньютона?
   

Задачи для самостоятельного решения

2.9; 2.12; 2.16; 2.25; 2.30 [3] или 2.6; 2.13; 2.53; 2.52; 2.2 [4].
Литература

1. 
   Савельев И.В. Курс общей физики, т.1.-М.:"Наука",-1977.-416с. (§5)
   
2. 
   Трофимова Т.И. Курс физики.-М.:"Высш.шк.",-1985.-432с. (§4)
   
3. 
   Волькенштейн В.С. Сб. задач по общему курсу физики.-М.: "Наука",-1985.-382 с.
   
4. 
   Чертов А.Г., Воробьёв А.А. Задачник по физике.-М.: "Высш.шк.",-1981.-496с.