3-алгоритмы ИНФОРМАТИКА. Конспект лекций по информатике и программированию для специальности 3514

• Название: Конспект лекций по информатике и программированию для специальности 3514
• Анкор: 3-алгоритмы ИНФОРМАТИКА.doc
• Дата: 25.02.2018
• Размер: 149 Kb.
• Имя файла: 3-алгоритмы ИНФОРМАТИКА.doc
• Тип: Конспект лекций; #15914

Министерство образования Российской Федерации

Московская Государственная академия приборостроения и информатики

Конспект лекций по информатике и программированию

для специальности 3514

Автор доц., к.т.н. Каширская Е.Н.
Москва, 2001

Часть 3. ОРГАНИЗАЦИЯ ДАННЫХ В ЭВМ И ОСНОВЫ ПРОГРАММИРОВАНИЯ

1. ВВЕДЕНИЕ В ПРОГРАММИРОВАНИЕ

1.1. Основные этапы решения задач на ЭВМ:

• 
  постановка задачи;
  
• 
  построение математических моделей;
  
• 
  разработка методики решения задач;
  
• 
  разработка алгоритма решения задачи;
  
• 
  составление программы по разработанному алгоритму;
  
• 
  ввод программы в ЭВМ;
  
• 
  отладка программы (поиск и исправление ошибок);
  
• 
  проведение расчетов по программе;
  
• 
  вывод результатов;
  
• 
  анализ результатов.
  

При составлении любого вида программы для ЭВМ понятие алгоритма является ключевым. Основным в процессе программирования является разработка алгоритма. Это один из наиболее сложных этапов решения задачи с использованием ЭВМ. В начале обучения программированию целесообразно не привязываться сразу к какому-либо языку, разрабатывать алгоритмы без записи на ЯПВУ, а, например, с помощью блок-схем или иным аналогичным способом. После такой "чистой" алгоритмизации проще перейти к записи того же алгоритма на определённом языке программирования.

Само слово «алгоритм» означает правило выполнения арифметических действий с использованием арабских цифр.

В средние века были две враждующие партии, среди приверженцев различных традиций счета. Абакисты считали на абаках, алгоритмики же использовали зачатки математической символики.

Слово «алгоритм» происходит от латинской формы написания имени математика IX века Аль-Хорезми, автор учебника арифметики, который сформулировал правила выполнения арифметических действий.

Первоначально под алгоритмом понимали только правила выполнения четырех арифметических действий над многозначными числами. В дальнейшем же это понятие стали использовать вообще для обозначения последовательности действий, приводящих к решению поставленной задачи.

Будем под алгоритмом решения задачи понимать систему правил, задающих строго определенную последовательность операций, приводящих к искомому результату за конечное число шагов.

Итак, алгоритм – это набор инструкций, который описывает, как некоторое задание может быть выполнено. Первоначально этот термин использовался для чисто численных процессов, но в вычислительной технике он приобрел более широкое значение.

Примеры алгоритмов в этом широком смысле встречаются в повседневной жизни: рецепт какого-нибудь блюда можно считать алгоритмом, описывающим процесс приготовления пищи, выкройку – алгоритмом изготовления одежды. Программы для ЭВМ являются алгоритмами, только выраженными некоторыми специальными средствами языка программирования.

Пять характеристик алгоритмов:

1. 
   вход алгоритма;
   
2. 
   выход алгоритма;
   
3. 
   определенность шагов алгоритма;
   
4. 
   выполнимость шагов;
   
5. 
   конечность.
   

Пример невыполнимого шага: присвоить Х значение, равное наибольшему вещественному числу, меньшему 1.

Это невозможно сделать, какое бы значение для Х мы не выбрали, всегда можно составить большее, добавив к десятичной части числа любую цифру: 0,999→0,9994 и т.д.

Пример. Алгоритм сложения столбиком: 315

⁺48

363

Указана последовательность действий, приводящих к результату за конечное число шагов. Можно дать точное словесное описание алгоритма:

Шаг 1. Ввод – любых двух слагаемых (из класса объектов, к которым применим алгоритм).

Шаг 2. Сложить цифры, стоящие в разрядах единиц; единицы полученного результата записать в разряд единиц суммы.

Шаг 3. Сложить цифры, стоящие в разрядах десятков и прибавить к ним единицу, если результат шага 2 не меньше десяти.

Шаг 4. То же для разряда сотен и т.д., пока не закончатся разряды слагаемых.

Шаг N. Вывод – значение суммы.

1.2. Схемы алгоритмов

Схема – это графическое изображение алгоритма. При ее построении содержимое каждого шага алгоритма записывается в произвольной форме внутрь блока, представленного геометрической фигурой. Порядок выполнения шагов указывается с помощью стрелок, соединяющих блоки.

Использование различных геометрических фигур отражает различный характер выполняемых действий.

В прямоугольнике (блок вычислений) записываются действия, в результате которых данные изменяют свои значения.

В ромб (блок сравнения) записывают условия, подлежащие проверке с целью выбора варианта продолжения работы.

Параллелограмм (блок ввода-вывода) содержит информацию о входных и выходных данных.

Овал означает начало или окончание вычислительного процесса.

Блок сравнения, в отличие от остальных, имеет 2 выхода – “да” и “нет”. Если условие, записанное внутри блока, выполняется, выход из него происходит по стрелке “да”, в противном случае – по стрелке “нет”.

Наиболее часто употребляемые символы схем алгоритмов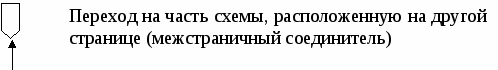

















Ручное управление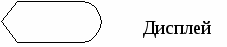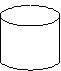


Магнитный диск


Основными алгоритмическими структурами (ОАС) являются следование, развилка и цикл. В более сложных случаях используются суперпозиции (вложения) ОАС.

Ниже приведены графические обозначения (обозначения на блок-схемах) ОАС.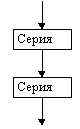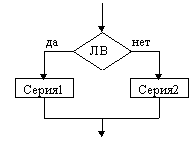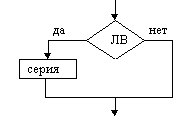



Структура Полная развилка Неполная

“следование” развилка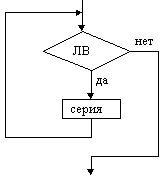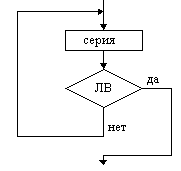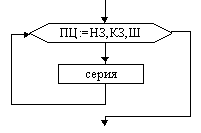


Цикл с предусловие Цикл с постусловием Цикл с параметром

(цикл ПОКА) (цикл ДО)
На схемах СЕРИЯ обозначает один или несколько любых операторов; УСЛОВИЕ есть логическое выражение (ЛВ) (если его значение ИСТИНА, переход происходит по ветви ДА, иначе — по НЕТ). На схеме цикла с параметром использованы обозначения: ПЦ — параметр цикла, НЗ — начальное значение параметра цикла, КЗ — конечное значение параметра цикла, Ш — шаг изменения параметра цикла.

Начало и конец алгоритма на блок-схемах обозначают овалом, вводимые и выводимые переменные записываются в параллелограмме.

В примерах мы будем использовать запись алгоритмов с помощью блок-схем и словесное описание.

1.3. Линейные алгоритмы

Линейным называется алгоритм, выполнение шагов которого происходит последовательно в порядке возрастания их номеров. В схеме он изображается последовательностью вычислительных блоков и блоков ввода-вывода. Простейшие задачи имеют линейный алгоритм решения. Это означает, что он не содержит проверок условий и повторений.
Общий вид линейного участка: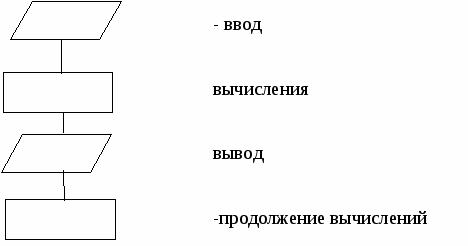


Пример 1. Пешеход шел по пересеченной местности. Его скорость движения по равнине v1 км/ч, в гору — v2 км/ч и под гору — v3 км/ч. Время движения соответственно t1, t2 и t3 ч. Какой путь прошел пешеход?

1. Ввести v1, v2, v3, t1, t2, t3. 2. S1 := v1 * t1. 3. S2 := v2 * t2. 4. S3 := v3 * t3. 5. S := S1 + S2 + S3. 6. Вывести значение S. 7. Конец.

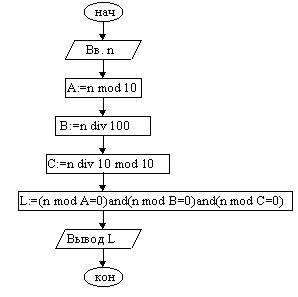
Для проверки работоспособности алгоритма необходимо задать значения входных переменных, вычислить конечный результат по алгоритму и сравнить с результатом ручного счета.

Пример 2. Дано натуральное трехзначное число n, в записи которого нет нулей. Составить алгоритм, который возвращает значение ИСТИНА, если верно утверждение: "число n кратно каждой своей цифре", и ЛОЖЬ — в противном случае.

1. Ввести число n 2. A := n mod 10 {разряд единиц} 3. B := n div 100 {разряд сотен} 4. C := n div 10 mod 10 {десятки} 5. L := (n mod A=0) and (n mod B=0) and (n mod C=0) 6. Вывод L 7. Конец

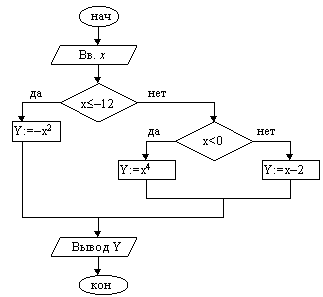
На приведенной выше схеме DIV и MOD соответственно операции деления нацело и получения остатка от целочисленного деления. В фигурных скобках записаны пояснения (комментарии) к операторам.

1.4. Разветвляющиеся алгоритмы (развилка)

Разветвляющимся называется алгоритм, в котором предусмотрено прохождение различных вариантов работы в зависимости от выполнения или не выполнения некоторого условия. В блок-схеме это условие записывается в ромб-блок сравнения.

Общая структура ветвления: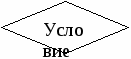

да

нет




Вар «да»

Вар. «нет»







Достаточно часто то или иное действие должно быть выполнено в зависимости от значения логического выражения, выступающего в качестве условия. В таких случаях используется развилка.

Пример 1. Вычислить значение функции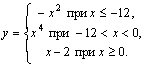

1. Ввести x. 2. Если x–12, то y:=–x2 3. Если x<0, то y:=x4 4. y := x–2 5. Вывести y 6. Конец

При тестировании алгоритмов с развилкой необходимо подбирать такие исходные данные, чтобы можно было проверить все ветви. В приведенном выше примере должно быть по крайней мере три тестовых набора.

Пример 2. Дано натуральное число n. Если число нечётное и его удвоение не приведет к выходу за 32767 (двухбайтовое целое число со знаком), удвоить его, иначе — оставить без изменения.

Чтобы удовлетворить условию удвоения, число n должно быть нечетным и меньше 16384.

1. Ввести число n 2. Если число n нечетное и меньше 16384, то n := n * 2 3. Вывод n 4. Конец

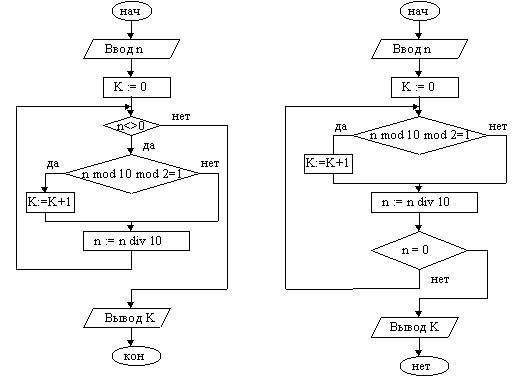
Рассмотренный пример иллюстрирует неполную развилку. Также следует отметить, здесь логическое выражение, являющееся условием, содержит 2 операнда.

1.5. Циклические алгоритмы (циклы)

Алгоритм циклической структуры – алгоритм, в котором предусмотрено выполнение одной и той же последовательности действий.

Циклом называется участок алгоритма, реализующий многократно повторяющееся при различных значениях параметров однотипные вычисления (например, расчеты по одной и той же формуле), Алгоритм, содержащий цикл, называется циклическим.

Циклический алгоритм позволяет существенно сократить объем программы.

Для организации цикла необходимо предусмотреть:

- задание начального значения параметра цикла – переменной, которая будет изменяться при повторениях цикла;

- изменение значения этой переменной перед каждым новым повторением цикла;

- проверку условия окончания повторений по значению параметра и переход к началу цикла, если повторения не закончены.

Пример 1. Вычислить сумму: S=1²+2²+3²+…+n²=∑i² ,

где n – заданное число.

Предлагается следующий алгоритм решения задачи.

Шаг 1. Ввести n.

Шаг 2. Положить S=0 (обнуление ячейки суммы).

Шаг 3. Положить i = 1.

Шаг 4. Вычислить i² и прибавит к текущему значению S: обозначение: S=S+i² .

Шаг 5. Увеличить i на 1; обозначение: i = i + 1.

Шаг 6. Сравнить i с n; если i < n, вернуться к шагу 4, иначе перейти к шагу 7.

Шаг 7. ВывестиS.

Шаг 8. Останов.

Основная повторяющаяся операция: S=S+i² выполняется при различных значениях i. Величина i называется параметром цикла. В рассмотренном примере параметр цикла изменяется от начального значения i = 1 до конечного i = n с шагом 1.

Варианты: 1) S=1²+3²+5²+…

2) S=1*2*3*…*n

Задача. Задача табулирование функции. Требуется построить таблицу значений функции y=f(x) на отрезке [a, b] с шагом h, т.е. вычислить значения функции в точках x=a, a+h, a+2h, … , b вывести их на печать.

Задача. Составить схему алгоритма вычисления 100 значений функции y=sin(ax)/x при xi=1,2,3,…,100. Очевидно, что для определения всех значений функции y необходимо 100 раз вычислять по этой формуле значения y и печатать их, изменяя каждый раз аргумент x на единицу. Цикл должен повторяться, пока x<100. Если х станет больше 100, то будет осуществлен выход из цикла, т.е. переход к следующему по порядку действию. Если какие-либо операторы необходимо выполнить несколько раз, то их не переписывают каждый раз заново, а организуют цикл.

Пример 2. Подсчитать количество нечетных цифр в записи натурального числа n.

Идея решения. Из заданного числа выбирать из младшего разряда цифру за цифрой до тех пор, пока оно не исчерпается, т.е. станет равным нулю. Каждую нечётную цифру учитывать.

1. Ввести число n 2. K := 0 {подготавливаем счётчик} 3. Если n = 0, переход к п. 4. Если n mod 10 mod 2 = 1, то K := K +1 5. n := n div 10 6. Переход к п. 3 7. Вывод K 8. Конец

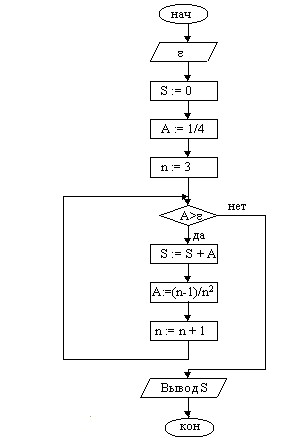
Задача решена двумя способами. Слева решение оформлено с использованием цикла с предусловием, справа — с постусловием.

Пример 3. Дана последовательность, общий член которой определяется формулой



Вычислить при n>2 сумму тех ее членов, которые больше заданного числа .

При решении задачи находится очередной член последовательно и, если он больше , добавляется к сумме.

1. Ввести  2. S := 0 3. A := 1/4 4. n := 3 5. Сравнить А с . Если A>=, переход к п. 10 6. S := S + A 7. A := (n-1)/(n*n) 8. n := n + 1 9. Переход к п. 5 10. Вывод S 11. Конец

В рассмотренных выше примерах количество повторений заранее неизвестно. В первом оно зависит от количества цифр в записи натурального числа, во втором — от числа .

В тех же случая, когда количество шагов известно из условия задачи, проще и предпочтительней использовать цикл с параметром.

Пример 4. Найти произведение первых k натуральных чисел, кратных трём.

При составлении алгоритма учтем, что первое натуральное число, кратное 3, есть тройка, а все последующие больше предыдущего на 3.

1. Ввод k 2. P := 1 {здесь накапливаем произведение} 3. T := 0 {здесь будут числа, кратные 3} 4. I := 1 5. Если I > k, переход к п. 10 6. T := T + 3 7. P := P * T 8. I := I + 1 9. Перейти к п. 5 10. Вывод P 11. Конец

Пример алгоритма.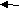





Другие примеры будут записаны уже на ЯПВУ. В настоящем же разделе предпринята попытка продемонстрировать, что изучение программирования разумно начинать собственно с разработки алгоритмов, не акцентируя первоначально внимания на записи алгоритма на том или ином языке программирования. В то же время сторонники структурного подхода к программированию предлагают придерживаться этого подхода и при программировании на уровне блок-схем.