|
|
Конспект урока Квадратичная функция. Конспект (квадратичная функция). Конспект урока по алгебре 8 класс функция yax 2 bxc, ее свойства и график Тема урока Функция yax 2 bxc, ее свойства и график Тип урока изучение нового материала Цели урока
КОНСПЕКТ УРОКА ПО АЛГЕБРЕ 8 КЛАСС
«ФУНКЦИЯ y=ax2+bx+c, ЕЕ СВОЙСТВА И ГРАФИК»
Тема урока: «Функция y=ax2+bx+c, ее свойства и график»
Тип урока: изучение нового материала
Цели урока:
- Обобщить понятие квадратичной функции, ее свойств путем знакомства со свойствами и графиком;
- Обозначить перспективу практического применения знаний о квадратичной функции.
Образовательная цель: изучить квадратичную функцию, её свойства и график, научиться находить координаты вершины параболы, ось симметрии параболы, научиться строить график квадратичной функции y=ax2+bx+c.
Воспитательная цель: создать условия для применения на уроке математики знаний, полученных в других предметных областях; развивать познавательную активность, самостоятельность, упорство в достижении цели, а также коммуникативные способности учащихся.
Развивающая цель: продолжить развитие культуры умственной деятельности (анализ, синтез, классификация, планирование), математическая речь
Планируемые образовательные результаты:
Предметные: знает функцию y=ax2+bx+c и ее свойства; знает ее график и умеет применять на практике эти знания.
Личностные: формирование познавательного интереса к предмету исследования, формирование устойчивой мотивации к изучению и закреплению материала.
Метапредметные:
а) Регулятивные: ставит учебную задачу на основе того, что уже известно и усвоено, и что подлежит усвоению, осознает качество и уровень усвоения.
б) Познавательные: определяет основную и второстепенную информацию, выделяет и формулирует проблему, ориентируясь на разные способы решения задачи.
в) Коммуникативные: использует адекватные языковые средства для отображения своих мыслей и чувств, описывает содержание совершаемых действий с целью ориентировки предметно-практической деятельности, проявляет готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции.
Оборудование: компьютер, интернет ресурс GEOGEBRA.COM, проектор с экраном, доска
Структура урока:
организационный момент;
актуализация знаний;
изучение нового материала;
обобщение и закрепление знаний; формирование умений применять полученные знания при выполнении индивидуальных заданий;
подведение итогов урока (домашнее задание, рефлексия);
Ход урока:
|
Этап урока
|
Действия учителя
|
Деятельность обучающихся
|
Формируемые УУД
|
1.
|
Организационный этап (1-2 мин.)
|
Здравствуйте, сегодня у нас урок по теме «Степенная функция».
Целью нашего урока является показать роль свойств степенной функции в процессе решения ряда математических, физических и экономических задач, а, следовательно, и роль этой функции и ее свойств в процессе сдачи ЕГЭ.
|
|
Личностные: готовность к выполнению норм и требований учителя
|
2.
|
Актуализация знаний (5-8 мин.)
|
Для начала вспомним определение функции:
Вопрос 1: Что такое функция?
Вопрос 2: Какие функции Вы знаете?
Все выше перечисленные функции относятся к элементарным функциям.
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций. Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.
Вопрос 3: Что называется графиком функции?
Задание: Обратите внимание, на эскизе представлен некий пейзаж. Постарайтесь среди данных линий найти графики функций.
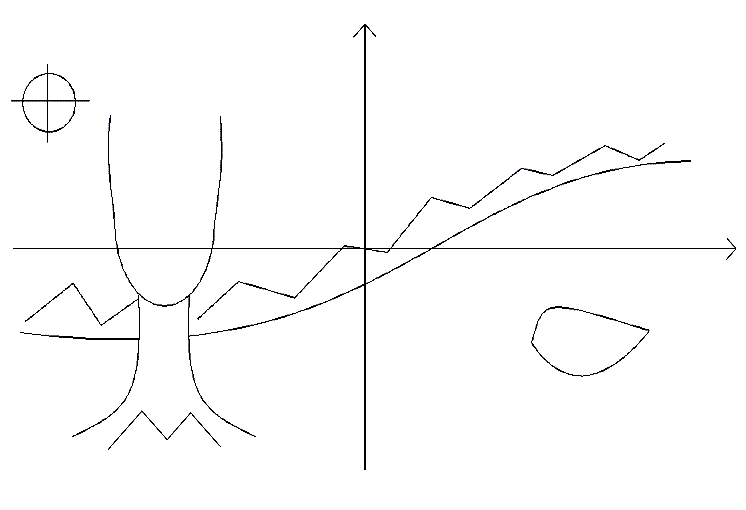
Вопрос 4: Так любое ли множество точек на координатной плоскости задает график функции?
Вопрос 5: А какие из этих линий относятся к графикам степенных функций?
Теперь давайте вспомним следующие функции, их графики и свойства:
y=x², y=x³, y=1/x ,y=√x или y=x½ , y=x
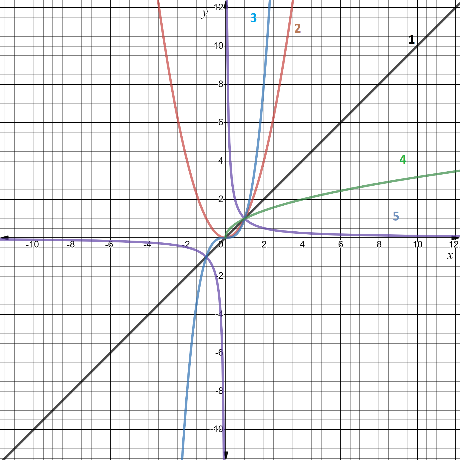
На рисунке изображены графики ряда степенных функций, обозначенные цифрами от 1 до 5). Давайте вспомним:
названия графиков и их соответствие алгебраической записи функции;
свойства изображенных функций (область определения, область значений, четность/нечетность).
Будем называть функцию, а вы же должны указать соответствующий ей график функции (или наоборот).
|
Ответ 1: Функция (отображение, оператор, преобразование) — соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.
Ответ 2:
Прямая пропорциональность.
Линейная функция.
Обратная пропорциональность.
Квадратичная функция.
Степенная функция.
Показательная функция.
Логарифмическая функция.
Тригонометрические функции.
Обратные тригонометрические функции.
Ответ 3:
Это геометрическое понятие в математике, дающее представление о геометрическом образе функции.
Задание: определяют графики функций
Ответ 4:
Нет, только такое множество, где каждому значению аргумента соответствует только одно значение функции
Посмотрите, насколько значимо изучение функции! Как мы видим на эскизе, графики функций встречаются не только в математике, но и в природе (горы, леса, деревья) – все, что нас окружает, состоит из графиков функций.
|
Регулятивные: планировать пути достижения целей; преобразовывать практическую задачу в познавательную; самостоятельно анализировать условия достижения цели на основе ориентиров, выделенных учителем.
Познавательные: устанавливать причинно-следственные связи; строить логическое рассуждение, включающее установление причинно-следственных связей.
Коммуникативные: аргументировать свою точку зрения; владеть устной речью.
|
3.
|
Изучение нового материала (30 мин)
|
И так, мы вплотную приблизились к пониманию степенной функции.
Степенная функция — это функция вида y = xp , где p — заданное действительное число (показатель степени).
К степенным функциям часто относят и функцию вида y=kxp , где k — некоторый (ненулевой) коэффициент.
На практике показатель степени почти всегда является целым или рациональным числом.
Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля).
Графики степенной функции при натуральном показателе p (=n, принадлежит множеству N – натуральных чисел) называются параболами порядка n.
При p=1 получается y=kx, называемая прямой пропорциональной зависимостью.
Графики функций вида y=xn где n — натуральное число, называются гиперболами порядка n.
При p=-1 получается функция y=x-1 или y=1/x называемая обратной пропорциональной зависимостью.
Если p=1/n ,то функция есть арифметический корень степени n.
С помощью интернет ресурса DESMOS.COM (известный графический и математический калькулятор) наглядно демонстрируем графическое отображения степенных функций, которые будем рассматривать ниже.
Ссылка на графический калькулятор: https://www.desmos.com/calculator?lang=ru
Ссылка на руководство пользователя редактором DESMOS на русском языке: https://desmos.s3.amazonaws.com/Desmos_User_Guide_RU.pdf
Свойства степенной функции:
1. Если показатель p = 2n — четное натуральное число:
область определения — все действительные числа, т. е. множество R;
множество значений — неотрицательные числа, т. е. y ≥ 0;
функция четная;
функция является убывающей на промежутке x ≤ 0 и возрастающей на промежутке x ≥ 0.
Пример функции с показателем p = 2n: y = x4, y =x16
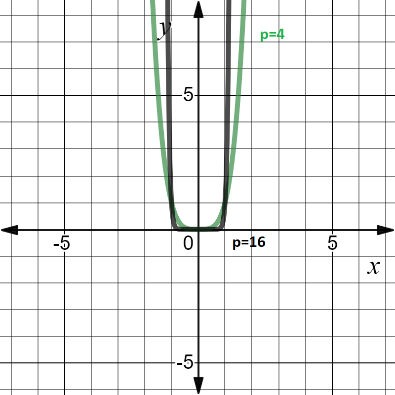
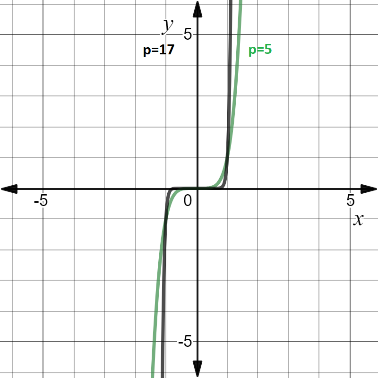
2. Если показатель p = 2n - 1 — нечетное натуральное число:
2.1. область определения — множество R;
2.2. множество значений — множество R;
2.3. функция нечетная;
2.4 функция является возрастающей на всей действительной оси.
Пример функции с показателем p = 2n - 1: y = x5 и y=x17
3. Если показатель p = -2n, где n — натуральное число:
3.1. область определения — множество R, кроме x = 0;
3.2. множество значений — положительные числа y > 0;
3.3. функция четная;
3.4. функция является возрастающей на промежутке x < 0 и убывающей на промежутке x > 0.
Пример функции с показателем p = -2n: y = 1/x2 и y = 1/x16
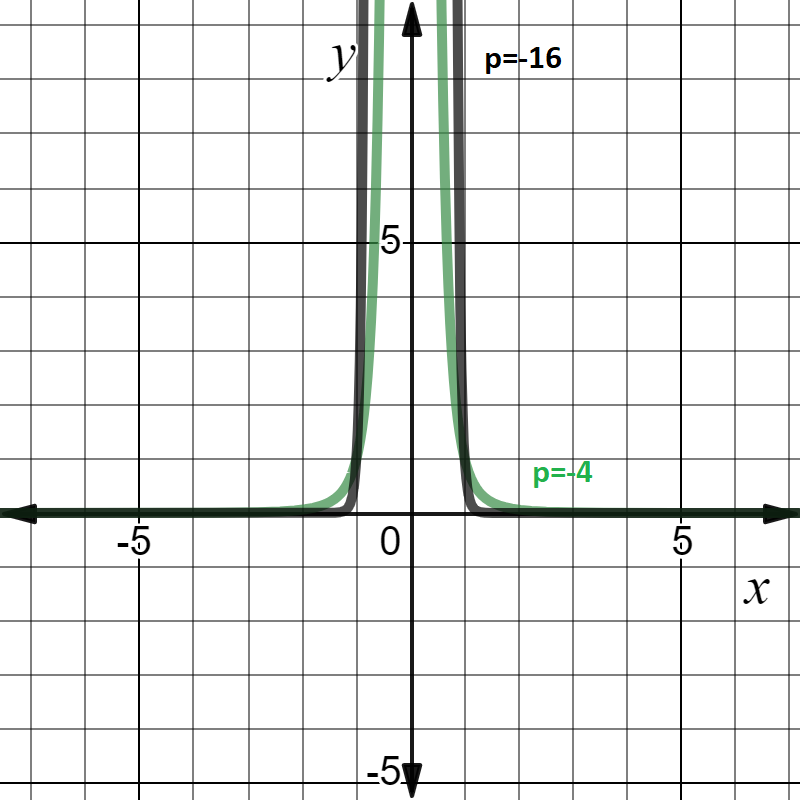
4. Если показатель p = -(2n - 1), где n — натуральное число:
4.1 область определения — множество R, кроме x = 0;
4.2 множество значений — множество R, кроме y = 0;
4.3 функция нечетная;
4.4 функция является убывающей на промежутках x < 0 и x > 0.
Пример функции с показателем p = -(2n - 1): y = 1/x3 и y = 1/x17
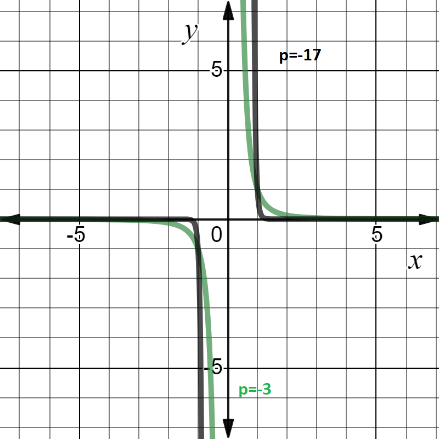
5. Если показатель p — положительное действительное нецелое число:
5.1. область определения зависит от четности знаменателя;
5.2 множество значений зависит от четности знаменателя;
5.3. функция является возрастающей/убывающей в зависимости от четности знаменателя;
Пример функции с показателем p, где p — положительное действительное нецелое число: y =x1/3 и y= x4/3.
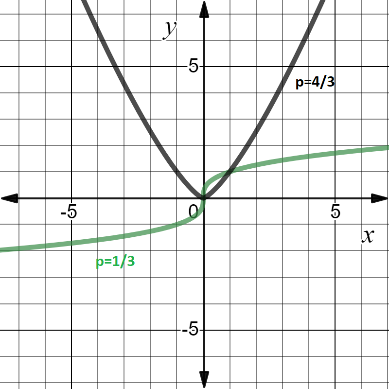
6. Если показатель p — отрицательное действительное нецелое число:
6.1. область определения — зависит от четности знаменателя и числителя, но x≠0;
6.2. множество значений — зависит от четности знаменателя и числителя, но y≠0;
6.3. функция является убывающей на промежутке x > 0.
Пример функции с показателем p, где p — отрицательное действительное нецелое число: y =x-4/3 и y= x -1/3.
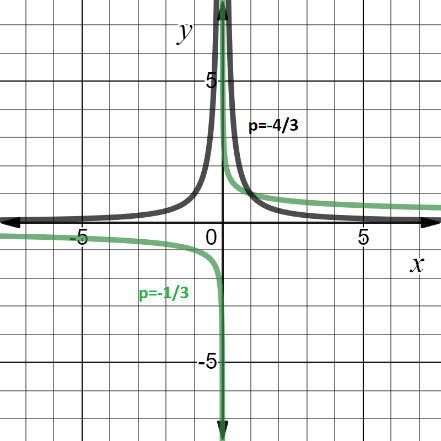
Рассмотрим задачу из экономики с использованием степенной функции:
Вкладчик поместил в банк 1000р. Банк ежегодно выплачивает вкладчику 3% от суммы вклада. Какую сумму денег s получит вкладчик через 2 года?
Решение: (проводится совместно с учениками на доске).
|
Ученики слушают всю теорию и записывают в тетрадь
Решение задачи
Дано:
s0=1000
r=3%
T=2 года
Найти: S-?
Решение:
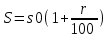 T T
S= 1000 (1+0.03)2= =1000*(1.03)2=
=1000*1.6=1060 р
Ответ: S=1060 р.
|
Личностные: готовность и способность к выполнению норм и обязанностей ученика; умение вести диалог на основе равноправных отношений и взаимного уважения и принятия; устойчивый познавательный интерес и становление смыслообразующей функции познавательного мотива.
Регулятивные: осуществлять целеполагание, преобразовывать практическую задачу в познавательную; самостоятельно анализировать условия достижения цели на основе ориентиров, выделенных учителем; самостоятельно оценивать правильность выполнения действий и вносить необходимые коррективы.
Познавательные: овладевать основами реализации проектно-исследовательской деятельности; строить логическое рассуждение, включающее установление причинно-следственных связей; создавать модели и схемы для решения задачи; осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве с одноклассниками; организовывать и планировать учебное сотрудничество со сверстниками, определять функции участников, способы взаимодействия; формулировать собственное мнение и аргументировать свою точку зрения; сравнивать разные точки зрения, прежде чем принимать решения и делать выбор; владеть устной речью.
|
4.
|
Домашнее задание (2 мин)
|
Подобрать задачи из жизни и других наук, в которых встречается степенная функция.
|
Ученики записывают домашнее задание
|
Личностные: готовность и способность к выполнению норм и требований школьной жизни, прав и обязанностей ученика.
|
7.
|
Рефлексия (3 мин)
|
Сегодня на уроке мы еще раз показали, насколько многогранно, изысканно и красиво используются свойства степенной функции в процессе решения математических задач, а также задач из разделов физики, экономики, в природе, в технике и т.д. Подводим итог урока, оцениваем деятельность класса и отдельных учащихся, просим учащихся выделить удавшиеся моменты, выясняем, что вызвало наибольшую трудность.
|
|
Личностные: умение вести диалог на основе равноправных отношений и взаимного уважения и принятия.
Познавательные: строить логическое рассуждение, включающее установление причинно-следственных связей; давать определение понятиям.
Коммуникативные: задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнером; использовать адекватные языковые средства для отображения своих чувств, мыслей, мотивов и потребностей; формулировать собственное мнение и позицию, аргументировать и координировать еѐ с позициями партнѐров в сотрудничестве при выработке общего решения в совместной деятельности.
|
|
|
|
 Скачать 258.51 Kb.
Скачать 258.51 Kb.








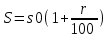 T
T