Методы принятия управленческих решений. Контрольная работа 110

Название	Контрольная работа 110
Дата	13.06.2022
Размер	0.53 Mb.
Формат файла
Имя файла	Методы принятия управленческих решений.docx
Тип	Контрольная работа #588610

Контрольная работа
№ 1-10. На предприятии необходимо запустить в эксплуатацию два комплекса взаимосвязанного оборудования. Запуск первого комплекса состоит из шести промежуточных этапов, а запуск второго комплекса – из четырех. Так как комплексы взаимосвязаны, то затраты на запуск очередного этапа одного комплекса зависят от того, на каком этапе находится запуск другого комплекса. Работы на двух комплексах одновременно не ведутся.

По заданной сетке затрат определите управление последовательностью этапов запуска комплексов, при котором общие расходы были бы наименьшими.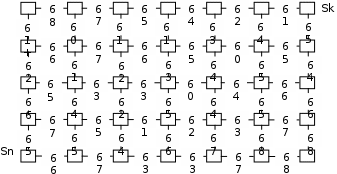

3.

Решение:
На оси абсцисс отмечены этапы запуска 1-го комплекса, на оси ординат – этапы запуска 2-го комплекса. Квадрат, расположенный в начале координат, отмечает начальное состояние системы Sn (начало запуска). Квадрат, расположенный в правом верхнем углу – конечное состояние системы Sk.

Осуществляем расчеты: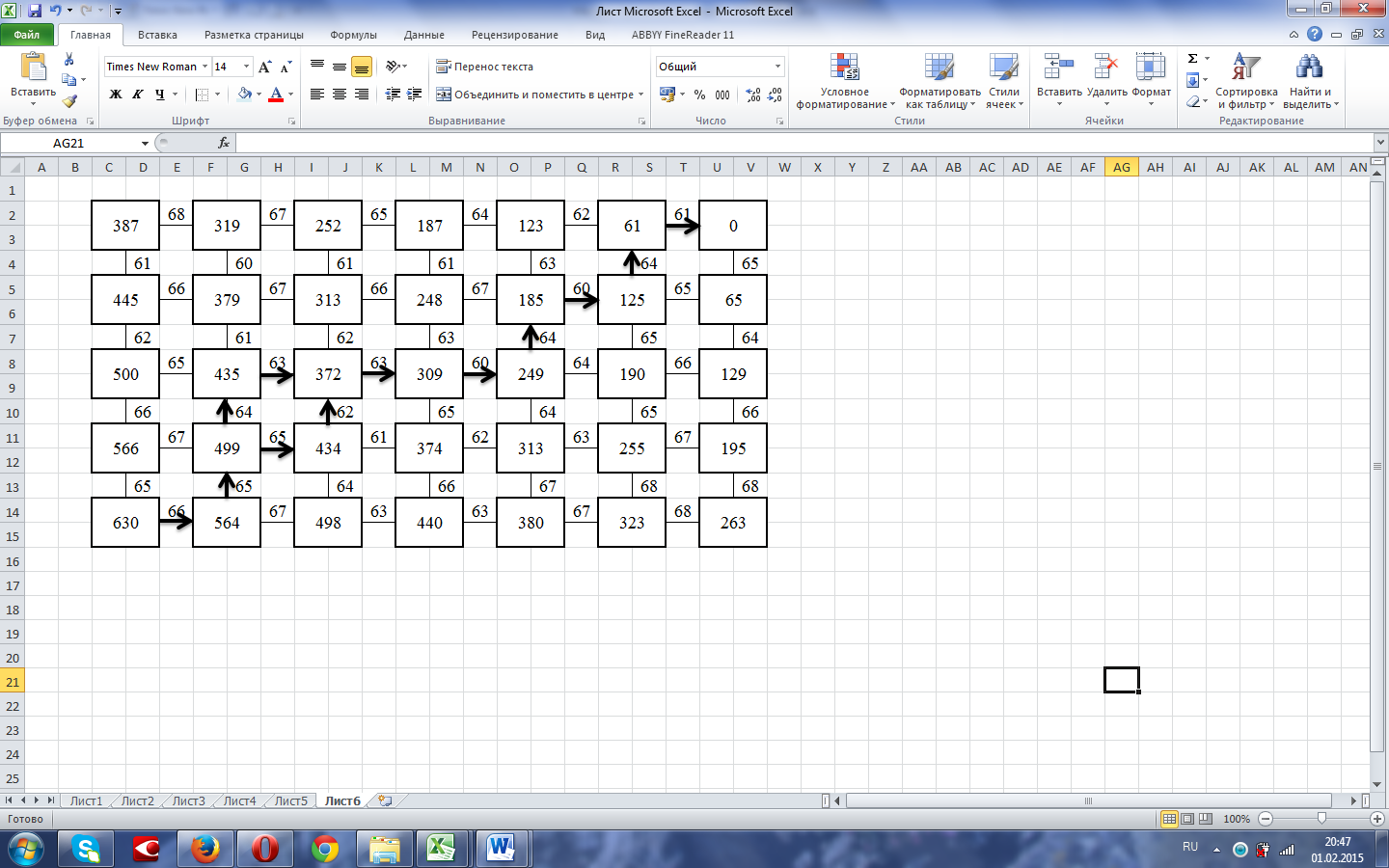

Таким образом, общие затраты на запуск комплексов составляют 630 ден. ед. При этом минимальные затраты дает два варианта последовательности:

первый вариант: 1-й этап 1-го комплекса → 1-й этап 2-го комплекса →2-й этап 2-го комплекса → 2-й этап 1-го комплекса → 3-й этап 1-го комплекса → 4-й этап 1-го комплекса → 3-й этап 2-го комплекса →5-й этап 1-го комплекса → 4-й этап 2-го комплекса → 6-й этап 1-го комплекса;

второй вариант: 1-й этап 1-го комплекса → 1-й этап 2-го комплекса →2-й этап 1-го комплекса → 2-й этап 2-го комплекса → 3-й этап 1-го комплекса → 4-й этап 1-го комплекса → 3-й этап 2-го комплекса →5-й этап 1-го комплекса → 4-й этап 2-го комплекса → 6-й этап 1-го комплекса.

№ 11-20. Определить верхнюю и нижнюю цены игры, а также оптимальные стратегии игроков, если задана матрица платежей.
14.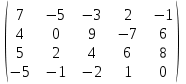

.

Решение:

Решение методом Минимакс

Рассмотрим игру двух лиц, интересы которых противоположны. Такие игры называют антагонистическими играми двух лиц. В этом случае выигрыш одного игрока равен проигрышу второго, и можно описать только одного из игроков.

Предполагается, что каждый игрок может выбрать только одно из конечного множества своих действий. Выбор действия называют выбором стратегии игрока.

Если каждый из игроков выбрал свою стратегию, то эту пару стратегий называют ситуацией игры. Следует заметить, каждый игрок знает, какую стратегию выбрал его противник, т.е. имеет полную информацию о результате выбора противника.

Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.

1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.

Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B₁	B₂	B₃	B₄	B₅	a = min(A_i)
A₁	7	-5	-3	2	-1	-5
A₂	4	0	9	-7	6	-7
A₃	5	2	4	6	8	2
A₄	-5	-1	-2	1	0	-5
b = max(B_i)	7	2	9	6	8

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = 2, которая указывает на максимальную чистую стратегию A₃.

Верхняя цена игры b = min(b_j) = 2.

Седловая точка (3, 2) указывает решение на пару альтернатив (A3,B2). Цена игры равна 2.

№ 21-30. Фирмы А и В конкурируют на рынке бытовой техники. Фирма А готова поставить на рынок изделия А₁, А₂ и А₃, фирма В – В₁, В₂ и В₃. Известна матрица А, показывающая долю освоенного рынка в случае соответствующей стратегии. Определите оптимальные стратегии поставок на рынок изделий фирмами А и В.

25 А =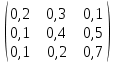

.

Решение:
Рассмотрим игру двух лиц, интересы которых противоположны. Такие игры называют антагонистическими играми двух лиц. В этом случае выигрыш одного игрока равен проигрышу второго, и можно описать только одного из игроков.

Предполагается, что каждый игрок может выбрать только одно из конечного множества своих действий. Выбор действия называют выбором стратегии игрока.

Если каждый из игроков выбрал свою стратегию, то эту пару стратегий называют ситуацией игры. Следует заметить, каждый игрок знает, какую стратегию выбрал его противник, т.е. имеет полную информацию о результате выбора противника.

Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.

1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.

Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B₁	B₂	B₃	a = min(A_i)
A₁	0.2	0.3	0.1	0.1
A₂	0.1	0.4	0.5	0.1
A₃	0.1	0.2	0.7	0.1
b = max(B_i)	0.2	0.4	0.7

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = 0.1, которая указывает на максимальную чистую стратегию A₁.

Верхняя цена игры b = min(b_j) = 0.2.

Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 0.1 ≤ y ≤ 0.2. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).

2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.

Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.

Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если a_ij ≥ a_kj для всех j Э N и хотя бы для одного j a_ij > a_kj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая.

Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M a_ij ≤ a_il и хотя бы для одного i a_ij < a_il. В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой.

С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₂ (все элементы столбца 1 меньше элементов столбца 2), следовательно, исключаем 2-й столбец матрицы. Вероятность q₂ = 0.

0.2	0.1
0.1	0.5
0.1	0.7

Стратегия A₃ доминирует над стратегией A₂ (все элементы строки 3 больше или равны значениям 2-ой строки), следовательно, исключаем 2-ую строку матрицы. Вероятность p₂ = 0.

0.2	0.1
0.1	0.7

Мы свели игру 3 x 3 к игре 2 x 2.

Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.

Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I.

3. Находим решение игры в смешанных стратегиях.

Запишем систему уравнений.

Для игрока I

0.2p₁+0.1p₂ = y

0.1p₁+0.7p₂ = y

p₁+p₂ = 1

Для игрока II

0.2q₁+0.1q₂ = y

0.1q₁+0.7q₂ = y

q₁+q₂ = 1

Решая эти системы методом Гаусса (решение см. ниже), находим:

y = 0.186

p₁ = 0.857 (вероятность применения 1-ой стратегии).

p₂ = 0.143 (вероятность применения 2-ой стратегии).

Оптимальная смешанная стратегия игрока I: P = (0.857; 0.143)

q₁ = 0.857 (вероятность применения 1-ой стратегии).

q₂ = 0.143 (вероятность применения 2-ой стратегии).

Оптимальная смешанная стратегия игрока II: Q = (0.857; 0.143)

Цена игры:

y = 0.186

Также решение можно найти по следующим формулам

Ответ: y=0.186

P(0.86, 0, 0.14)

Q(0.86, 0, 0.14)
№ 31-40. Фирма выпускает два вида скоропортящейся продукции М и N. Себестоимость единицы продукции М составляет а₁2 рублей, единицы продукции N – а_{2 –}1,5 рублей. Розничная цена единицы продукции М равна с₁3,3 рубля, единицы продукции N – с₂ – 2,7 рубля. Если продукция не реализуется в течение одного дня, то она дешевеет в три раза. Реализация продукции зависит от погоды: в хорошую погоду реализуется т₁1500 единиц продукции М и п₁ 5000 единиц продукции N; в плохую погоду реализуется т₂ – 4000 единиц продукции М и п₂ 1500 единиц продукции N. На реализацию товара в день расходовалось 1000 рублей. Составить матрицу платежей для отыскания наибольшей гарантированной прибыли.
36. а₁ = 2,0; а₂ = 1,5; с₁ = 3,3; с₂ = 2,7; т₁ = 1500; п₁ = 5000; т₂ = 4000; п₂ = 1500.
Решение:

Рассматривая организацию и природу как двух игроков (в дальнейшем первого игрока будем называть Организация, а второго – Природа) можно оценить прибыль организации при совпадении и несовпадении стратегий игроков.

Чистые стратегии Организации:

S₁ – расчет на хорошую погоду;

S₂ – расчет на плохую погоду.

Чистые стратегии Природы:

S₃ – хорошая погода;

S₄ – плохая погода.

Цена игры – прибыль Организации, которая рассчитывается по формуле:

Р = S - С,

где Р – прибыль, ден. ед.;

S – выручка, ден. ед.;

С – затраты на закупку и реализацию продукции, ден. ед.

Рассмотрим возможные сочетания стратегий игроков.

1 игра. Стратегии: Организации – S₁, природы – S₃.

В расчете на хорошую погоду Организация произведет и реализует 1500 единиц продукции M и 5000 единиц продукции N.

С₁ = 1500×2 + 5000×1,5 + 1000 = 11500 ден. ед.

S₁ = 1500×3,3 + 5000 × 2,7 = 18450 ден. ед.

Р₁ = 18450 - 11500 = 6950 ден. ед.

2 игра. Стратегии: Организации – S₁, природы – S₄.

В расчете на хорошую погоду Организация произведет и реализует 1500 единиц продукции M и 5000 единиц продукции N, но реализует ее не в первый день, по цене в 3 раза ниже розничной.

S₂ = 1500 × 1,1 + 5000 × 0,9 = 6150 ден. ед.

Р₂ = 6150- 11500 = -5350 ден. ед. (убыток).

3 игра. Стратегии: Организации – S₂, природы – S₃.

В расчете на плохую погоду Организация произведет и реализует 4000 единиц продукции M и 1500 единиц продукции N.

С₃ = 4000 × 2 + 1500 × 1,5 + 1000 = 11250 ден. ед.

S₃ = 4000 × 3,3 + 1500 × 2,7 = 17250 ден. ед.

Р₃ = 17250 - 11250 = 6000 ден. ед.

4 игра. Стратегии: Организации – S₂, природы – S₄.

В расчете на плохую погоду Организация произведет и реализует 4000 единиц продукции M и 1500 единиц продукции N, но реализует ее не в первый день, по цене в 3 раза ниже розничной.

S₄ = 4000 × 1,1 + 1500 × 0,9 = 5750 ден. ед.

Р₄ = 5750 -11250 = -5500 ден. ед.(убыток)

Подобного рода рассуждения позволяют сформировать так называемую платежную матрицу игры, в ячейках которой на пересечении стратегий игроков указывается выигрыш одного из игроков (в нашем случае прибыль Организации):

Таблица 1

Платежная матрица игры, ден. ед.

Игроки	Погода
Игроки	S3	S4
S1	6950	-5350
S2	6000	-5500

Критерий Байеса.

По критерию Байеса за оптимальные принимается та стратегия (чистая) A_i, при которой максимизируется средний выигрыш a или минимизируется средний риск r.

Считаем значения ∑(a_ijp_j)

∑(a_1,jp_j) = 6950*0.5 + (-5350)*0.5 = 800

∑(a_2,jp_j) = 6000*0.5 + (-5500)*0.5 = 250

A_i	П₁	П₂	∑(a_ijp_j)
A₁	3475	-2675	800
A₂	3000	-2750	250
p_j	0.5	0.5

Выбираем из (800; 250) максимальный элемент max=800

Вывод: выбираем стратегию N=1.

Критерий Вальда.

По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.

a = max(min a_ij)

Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.

A_i	П₁	П₂	min(a_ij)
A₁	6950	-5350	-5350
A₂	6000	-5500	-5500

Выбираем из (-5350; -5500) максимальный элемент max=-5350

Вывод: выбираем стратегию N=1.

Критерий Севиджа.

Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:

a = min(max r_ij)

Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.

Находим матрицу рисков.

Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b_j = max(a_ij) характеризует благоприятность состояния природы.

1. Рассчитываем 1-й столбец матрицы рисков.

r₁₁ = 6950 - 6950 = 0; r₂₁ = 6950 - 6000 = 950;

2. Рассчитываем 2-й столбец матрицы рисков.

r₁₂ = -5350 - (-5350) = 0; r₂₂ = -5350 - (-5500) = 150;

A_i	П₁	П₂
A₁	0	0
A₂	950	150

Результаты вычислений оформим в виде таблицы.

A_i	П₁	П₂	max(a_ij)
A₁	0	0	0
A₂	950	150	950

Выбираем из (0; 950) минимальный элемент min=0

Вывод: выбираем стратегию N=1.

Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия S₁S₃.
№ 41-50. Построить и упростить сетевой график комплекса работ, состоящий из 15 событий и 25 работ.

47. (0,1), (0,3), (0,4), (1,2), (1,9), (2,6), (2,11), (3,4), (4,2), (4,5), (4,7), (4,9), (5,6), (5,8), (6,12), (7,8), (7,13), (8,10), (9,10), (10,11), (10,12), (10,13), (11,14), (12,14), (13,14).
Решение:

Построим сетевой график

После построения сетевого графа его необходимо упорядочить и перенумеровать все события, приведя их в соответствие с их новым порядком выполнения комплекса работ.

Упорядочить сетевой граф значит так расположить события и работы, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Для упорядочивания сетевого графа используем метод последовательного вычеркивания дуг, который выполняется по следующему алгоритму:

Отыскать на сетевом графе начальное событие и присвоить ему ранг ноль.
Из сетевого графа мысленно вычеркиваются все работы, исходящие из начального события и вновь отыскиваются события, не имеющие предшествующих работ. Этим событиям (их может быть несколько) присваивается ранг единица. Все события первого ранга характеризуются тем, что число работ, соединяющих их с исходным событием, равно одному.
Далее из сетевого графа вновь мысленно вычеркиваются все работы, исходящие из события ранга i и вновь отыскиваются события, не имеющие предшествующих работ. Им присваивается ранг i + 1.
После завершения распределения всех событий по рангам перенумеровываем события с соблюдением двух условий:

а) события в графе нумеруются слева направо (от начального к конечному);

б) события одного ранга нумеруются сверху вниз в соответствии с графическим представлением событий одного ранга.

№ 51-60. Даны оценки времени выполнения работ сетевого графа. Требуется:

а) построить и упорядочить сетевой граф;

б) построить линейную диаграмму проекта;

в) определить критический путь и его длину.
58. t(0,1)=6, t(0,2)=7, t(0,6)=8, t(1,2)=4, t(1,4)=5, t(1,6)=3, t(2,3)=2, t(2,9)=10, t(3,7)=1, t(4,3)=9, t(4,5)=7, t(5,8)=6, t(6,5)=4, t(7,9)=5, t(8,9)=3.
Решение:

Решение графическим способом (секторальным методом)

При этом способе кружок сетевого графика, обозначающий событие, делится на четыре сектора. В верхнем ставится номер события i, в левом – наиболее раннее из возможных время свершения события t_p(i), в правом – наиболее позднее из допустимых время свершения события t_п(i), в нижнем – резерв времени данного события R(i).
Раннее время свершения события t_p(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i.
1. Послойно, переходя от исходного события до конечного, определим t_p(i). Всегда для начального события t_p(i) = 0 (рисунок 1).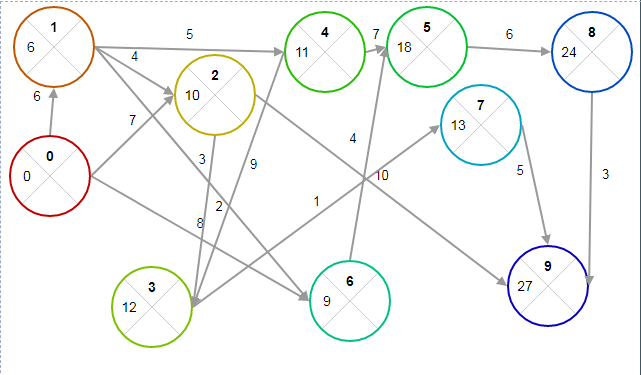

2. Находим позднее из допустимых время свершения события tп(i) (рисунок 2).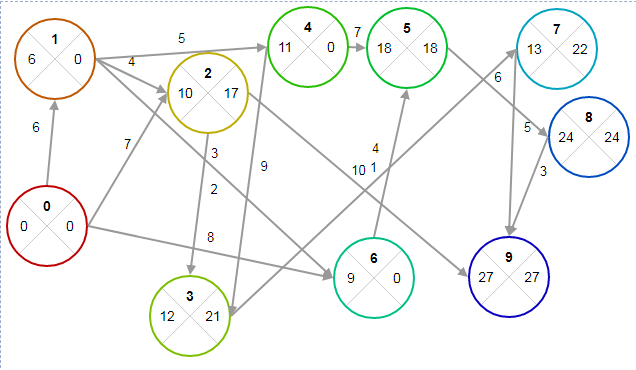

3. Определяем резерв времени данного события R(i) = tп(i) - tp(i) (рисунок 3).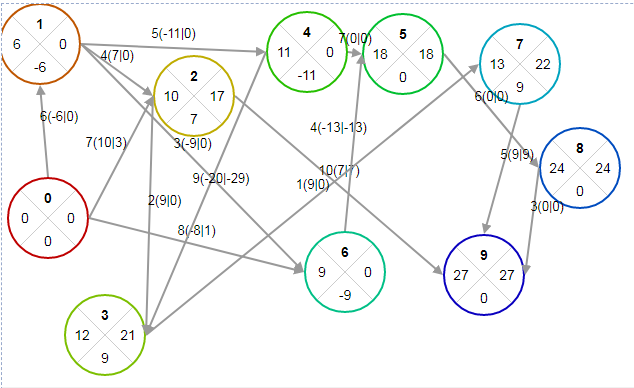

На рисунке 3 резервы времени работ обозначены в круглых скобках следующего формата: d(RijП|RijC)
2. Построим линейную диаграмму проекта, диаграмму Гранта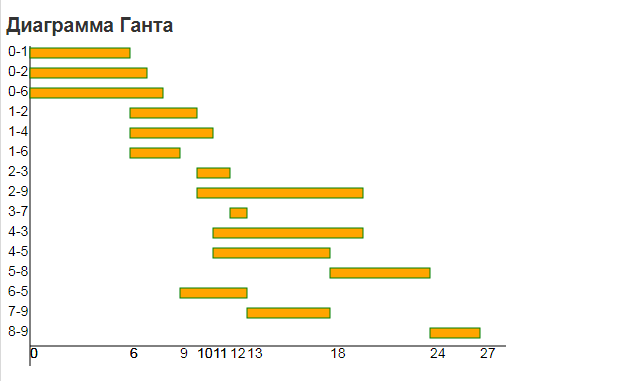

3. определить критический путь и его длину.