Главная страница
Медицина
Финансы
Экономика
Биология
Ветеринария
Сельское хозяйство
Юриспруденция
Право
Языкознание
Языки
Логика
Философия
Религия
Этика
Политология
Социология
История
Информатика
Вычислительная техника
Физика
Математика
Промышленность
Энергетика
Искусство
Культура
Химия
Электротехника
Связь
Автоматика
Геология
Экология
Начальные классы
Строительство
образование
Механика
Воспитательная работа
Русский язык и литература
Дошкольное образование
Реферат
Урок
Отчет
Программа
Закон
Курсовая
Задача
Занятие
Решение
Лекция
Протокол

контрольные работы. Контрольная работа 1 (Никольский) Алгебра 10 Никольский Контрольная 1 к вариант 3 (транскрипт)


Скачать 3.02 Mb.
НазваниеКонтрольная работа 1 (Никольский) Алгебра 10 Никольский Контрольная 1 к вариант 3 (транскрипт)
Анкорконтрольные работы
Дата06.04.2023
Размер3.02 Mb.
Формат файлаdocx
Имя файлаконтрольные работы.docx
ТипКонтрольная работа
#1040936

Алгебра 10 Никольский Контрольные работы

. Используется при работе по УМК Никольский. Цитаты из пособия «Алгебра и начала математического анализа. Дидактические материалы. 10 класс : базовый и углубленный уровни / Потапов, Шевкин» использованы в учебных целях. Ответы адресованы родителям. Алгебра 10 Никольский Контрольная 1 + ответы.


Алгебра и начала анализа. 10 класс
Контрольная работа № 1 (Никольский)

Алгебра 10 Никольский Контрольная 1




К-1. Вариант 3 (транскрипт)

  1. Упростите выражение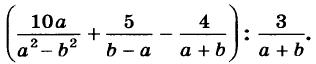


  2. Решите уравнение (2х + 7)/(х2 + 2x) – (x – 1)/(х2 + 6x + 8) = 0

  3. Решите неравенство: а) (x + 1)(x + 3)/(x – 2) < 0; б) (х2 – 4x + 4)/(х2 – x – 20) ≥ 0.

  4. * а) Упростите выражение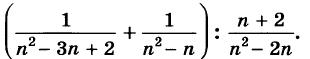

    б) Найдите значение полученного выражения при n = 2.

  5. * Докажите справедливость неравенства:
    а) х2 +y2 – 6х + 4у +13 ≥ 0; б) х4 + 13х2 – 6х + 6 > 0; в) х2 + 3 > √(х4 + 6х2 + 8).

  6. * Решите уравнение х4 + 4х3 – 2х2 – 12х + 9 = 0.

  7. * К трехзначному числу приписали цифру 3 сначала справа, потом слева, получились два числа, разность которых равна 3114. Найдите это трехзначное число.

К-1. Вариант 4 (транскрипт)

  1. Упростите выражение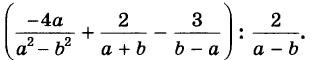


  2. Решите уравнение (2х + 6)/(х2 + x) – (х – 3)/(х2 + 3x + 2) = 0.

  3. Решите неравенство: а) (x + 1)(x – 1)/(x + 4) < 0; б) (х2 – 6x + 9)/(х2 – 4x – 5) ≥ 0.

  4. * а) Упростите выражение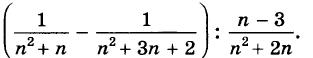

    б) Найдите значение полученного выражения при n = 0.

  5. * Докажите справедливость неравенства:
    а) х2 + у2 + 4х – 6у +13 ≥ 0; б) х4 + 10х2 – 4х + 14 > 0; в) х2 + 4 > √(х4 + 8х2 + 15).

  6. * Решите уравнение х4 – 4х3 – 2х2 + 12x + 9 = 0.

  7. * К трехзначному числу приписали цифру 2 сначала справа, потом слева, получились два числа, разность которых равна 4113. Найдите это трехзначное число.

 


Ответы на контрольную работу



 

Алгебра и начала анализа. 10 класс
Контрольная работа № 2 (Никольский)

Алгебра 10 Никольский Контрольная 2



К-2. Вариант 3 (транскрипт)

  1. Верно ли равенство: а) 10√(410) = 4; б) 10√(–5)10 = 5; в) 10√(610) = –6; г) 10√(–7)10 = –7?

  2. Избавьтесь от иррациональности в знаменателе дроби:
    а) 5 / 3√4; б) 3√6 / 3√(6 + 1); в) 3 / (3√49 + 3√7 + 1)

  3. Вычислите: а) 4√(20022 + 2 • 2002 • 498 + 4982);
    б) 3√(20013 – 3 • 20012 • 189 + 3 • 2001 • 1892 – 1893).

  4. Упростите выражение (6√а – 6√b)(3√a +6√ab + 3√b)(√a + √b).

  5. * Вычислите


  6. * Найдите значение выражения 3√(x • 4√(x • √x)) при x = 11√(1258).

  7. * Моторная лодка проходит расстояние между пристанями А и В по течению реки за 20 мин, а против течения за 1 ч. Во сколько раз собственная скорость моторной лодки больше скорости течения реки?

К-2. Вариант 4 (транскрипт)

  1. Верно ли равенство: a) 8√(58) = –5; б) 8√(68)= 6; в) 8√(–7)8 = –7; г) 8√(–8)8 = 8?

  2. Избавьтесь от иррациональности в знаменателе дроби:
    а) 2 / 3√9; б) 3√7 / 3√(7 – 1); в) 5 / (3√36 – 3√6 + 1).

  3. Вычислите: а) 4√(20012 – 2 • 2001 • 401 + 4012);
    б) 3√(17993 + 3 • 17992 • 203 + 3 • 1799 • 2032 + 2033).

  4. Упростите выражение (√x – √у)(6√x + 6√у)(3√x – 6√xу + 3√у).

  5. * Вычислите


  6. * Найдите значение выражения 3√(х • √(х • 4√х)) при x = 13√(278) ?

  7. * Моторная лодка проходит расстояние между пристанями А и В по течению реки за 25 мин, а против течения за 50 мин. Во сколько раз собственная скорость моторной лодки больше скорости течения реки?

 

Ответы на контрольную работу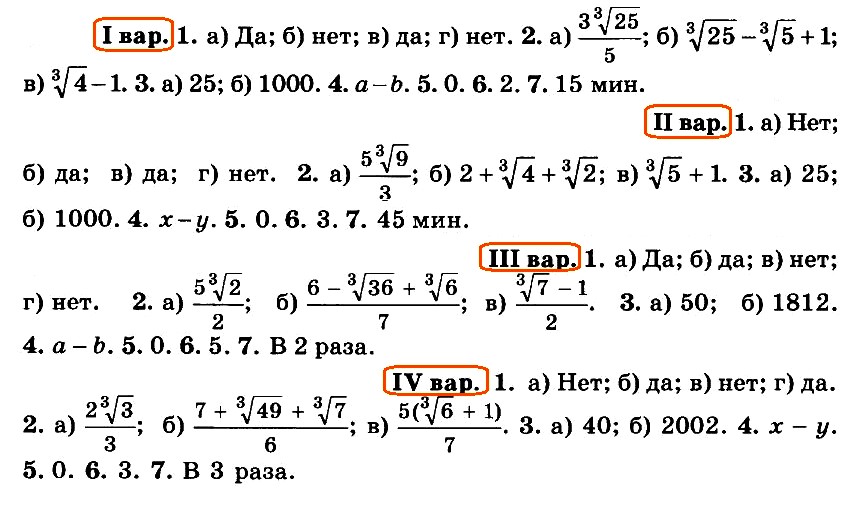



Алгебра и начала анализа. 10 класс
Контрольная работа № 3 (Никольский)

Алгебра 10 Никольский Контрольная 3



К-3. Вариант 3 (транскрипт)

  1. Найдите значение выражения (а1/2 : а2/3)30 при а = (1/2)–2/5.

  2. Вычислите (21/3 • 9–1/3) / (6–2/3 • 43/2).

  3. Постройте график функции и перечислите свойства этой функции: а) у = 4х; б) у = (1/5)х.

  4. Упростите выражение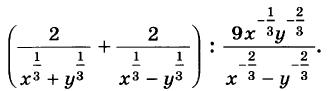 

  5. * Упростите выражение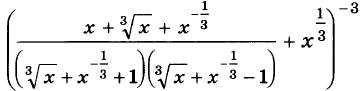
    и найдите его значение при х = 0,125.

  6. * Вычислите предел последовательности: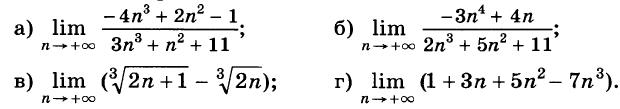


  7. * Четыре ученика, работая совместно с одинаковой производительностью, выполнили задание за некоторый срок. Один мастер и один ученик, работая совместно, выполнили бы это задание за 4/3 того же срока. Во сколько раз производительность мастера больше производительности ученика?

К-3. Вариант 4 (транскрипт)

  1. Найдите значение выражения (а1/4 : а1/2)20 при а = (3/10)–2/5.

  2. Вычислите (23/2 • 6–1/2) / (9–1/6 • 35/6).

  3. Постройте график функции и перечислите свойства этой функции: а) у = 5х; б) у = (1/4)х.

  4. Упростите выражение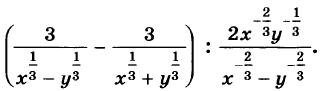 

  5. * Упростите выражение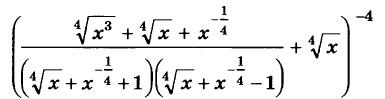
    и найдите его значение при х = 0,0125.

  6. * Вычислите предел последовательности: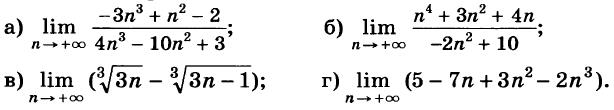


  7. * На четырех старых станках, работающих совместно с одинаковой производительностью, выполнили задание за некоторый срок. На одном новом и одном старом станках, работающих совместно, выполнили бы это задание за 0,8 того же срока. Во сколько раз производительность нового станка больше производительности старого станка?

 

Ответы на контрольную работу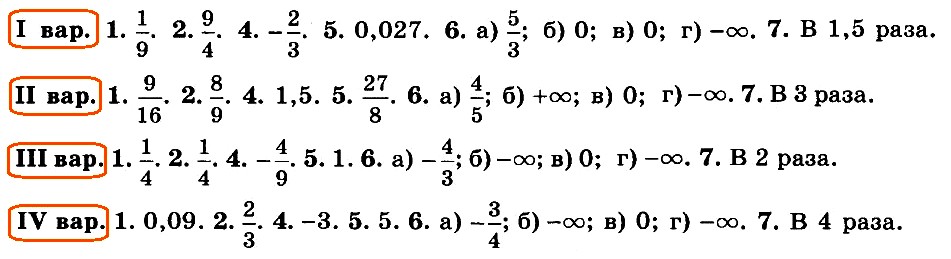



 

Алгебра и начала анализа. 10 класс
Контрольная работа № 4 (Никольский)

Алгебра 10 Никольский Контрольная 4



К-4. Вариант 3 (транскрипт)

  1. Вычислите: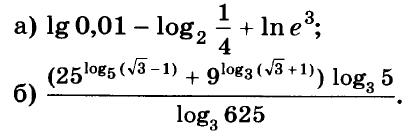


  2. Решите уравнение: а) 8 • (9/4)x – 30 • (3/2)x + 27 = 0; б) log2 х + 6log4 х + 9log8 х = 14.

  3. Решите неравенство: а) (1/3)x+2 + 5(1/3)x+1 – (1/3)x < 7; б) (log2 х)2 – 2lоg2 х – 3 ≤ 0.

  4. * Докажите числовое равенство log9(6√6 – 15)2 +log27(6√6 + 15)3 = 2.

  5. * Вычислите значение числового выражения (√5)log2 3 : (√3)log2 5

  6. * Решите уравнение (√2 – 1)x + (√2 + 1)x – 2 = 0.

  7. * Некоторое число деталей токарь должен обточить к намеченному сроку. За 6 ч он выполнил три четверти задания, а остальные детали обточил его ученик, который обтачивал на 6 деталей в час меньше, чем токарь. В результате задание было выполнено на 1 ч 20 мин позже намеченного срока. Сколько деталей обточили токарь и его ученик вместе?

К-4. Вариант 4 (транскрипт)

  1. Вычислите: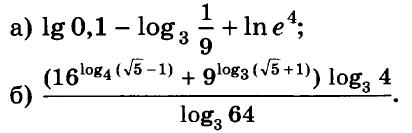


  2. Решите уравнение: a) 27 • (4/9)x – 30 • (2/3)x + 8 = 0; б) log3 x + 4log9 x + 6log27 x = 10.

  3. Решите неравенство: а) (1/2)x+2 + 3 • (1/2)x+1 – (1/2)x < 3; б) (log3 x)2 + 2log3 х – 3 < 0.

  4. * Докажите числовое равенство log4(4√6 – 10)2 + log8(4√6 + 10)3 = 2.

  5. * Вычислите значение числового выражения (√2)log5 3 : (√3)log5 2.

  6. * Решите уравнение (2 – √З)x + (2 + √3)x – 2 = 0.

  7. * Некоторое число деталей токарь должен обточить к намеченному сроку. За 4 ч он выполнил две трети задания, а остальные детали обточил его ученик, который обтачивал на 5 деталей в час меньше, чем токарь. В результате задание было выполнено на 1 ч 15 мин позже намеченного срока. Сколько деталей обточили токарь и его ученик вместе?



 

Ответы на контрольную работу



Алгебра и начала анализа. 10 класс
Контрольная работа № 5 (Никольский)

Алгебра 10 Никольский Контрольная 5




К-5. Вариант 3 (транскрипт)

  1. Вычислите: a) sin 30° + √6 cos 45° sin 60° – tg 30° ctg 150° + ctg 45°; б) cos π/3 – √2 sin 3π/4 + √3 tg π/3.

  2. Упростите выражение: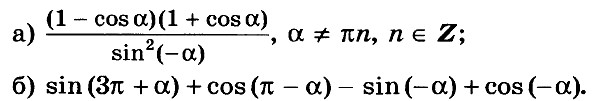


  3. Вычислите: а) (sin2 а – cos2 а)2+ 4 sin2 а cos2 а; б) tg a + ctg a, если sin a cos а = 0,3.

  4. Найдите все такие углы а, для каждого из которых выполняется равенство: а) sin a = –√3/2; б) cos a = √2/2; в) tg a = √3/3; г) ctg a = –√3.

  1. * Вычислите: а) tg2 a + ctg2 а, если tg a + ctg a = 4;
    б) 1 – 2/(tg a + ctg a), если cos a – sin a = –1/3.

  2. * Вычислите arcsin 1 – arccos √3/2 – (arctg (–√3/3)) / (arcctg (–√3).

  3. * Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 60% большей. На сколько процентов время движения оказалось меньше запланированного?

К-5. Вариант 4 (транскрипт)

  1. Вычислите: а) cos 60° – √6 cos 30° sin 45° + ctg 30° tg 150° – tg 45°;
    б) sin π/6 + √2 cos 3π/4 – √3 ctg π/3.

  2. Упростите выражение: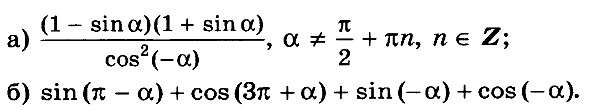


  3. Вычислите: а) (cos2 a – sin2 a)2 + 4 sin2 a cos2 a; б) tg a +ctg a, если sin a cos a = 0,6.

  4. Найдите все такие углы а, для каждого из которых выполняется равенство:
    a) sin a = √2/2; б) cos a –1/2; в) tg a = –√3/3; г) ctg a = √3.

  5. * Вычислите: а) tg2 a + ctg2 а, если tg a – ctg a = – 4; б) 1 – 2/(tg a + ctg a), если cos a + sin a = 1/3.

  6. * Вычислите arcsin √3/2 – arccos 1 + (arctg (–√3)) / (arcctg (–√3/3).

  7. * Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 75% большей. На сколько процентов время движения оказалось меньше запланированного?



 

Ответы на контрольную работу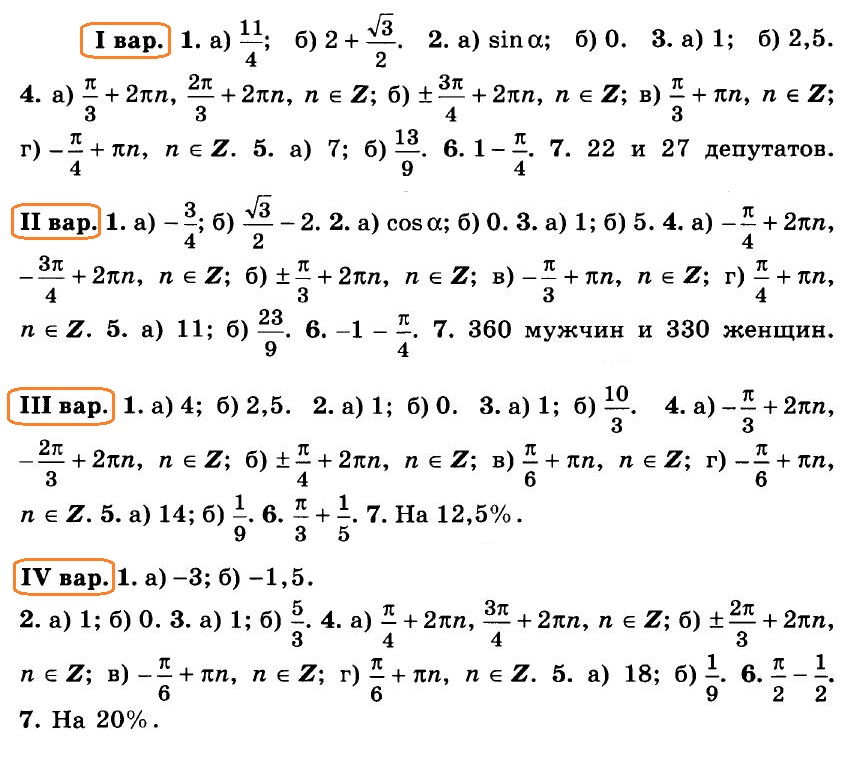



Алгебра и начала анализа. 10 класс
Контрольная работа № 6 (Никольский)

Алгебра 10 Никольский Контрольная 6



К-6. Вариант 3 (транскрипт)

  1. Упростите выражение: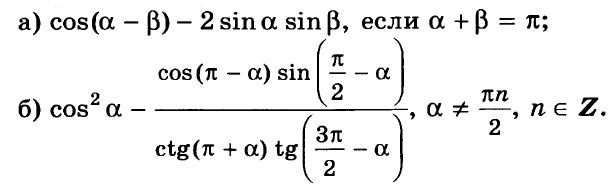


  2. Вычислите (sin 68° + cos 38°)2 + (sin 38° – cos 68°)2.

  3. Известно, что cos а = – 5/13, π < а < 3π/2. Вычислите: a) sin a; б) sin 2а; в) cos 2а.

  4. Постройте график функции у = (sin Зх cos 2х – sin 2х cos Зх) / (cos 3x cos 2х + sin Зх sin 2х).

  5. * Вычислите 2 cos 37° cos 23° – sin 76°.

  6. * Докажите справедливость равенства cos π/7 cos 2π/7 cos 4π/7 = –1/8.

  7. * Велосипедист и мотоциклист одновременно отправились навстречу друг другу из городов Л и В. После встречи мотоциклист прибыл в город В через 1 ч, а велосипедист прибыл в город А через 9 ч. Во сколько раз скорость мотоциклиста больше скорости велосипедиста?

К-6. Вариант 4 (транскрипт)

  1. Упростите выражение:


  2. Вычислите (cos 32° + cos 28°)2 + (sin 32° – sin 28°)2.

  3. Известно, что sin a = –12/13, 3π/2 < a < 2 π. Вычислите: а) cos а; б) sin 2а; в) cos 2а.

  4. Постройте график функции у = (cos 4x cos 3x + sin 4x sin 3x) / (sin 4x cos3x – sin 3x cos 4x).

  5. * Вычислите 2 sin 34° sin 26° – sin 82°.

  6. * Докажите справедливость равенства cos π/9 cos 2π/9 cos 4π/9 = 1/8.

  7. * Велосипедист и пешеход одновременно отправились навстречу друг другу из городов А и В. После встречи велосипедист прибыл в город В через 1 ч, а пешеход пришел в город А через 4 ч. Во сколько раз скорость велосипедиста больше скорости пешехода?



 

Ответы на контрольную работу




Алгебра и начала анализа. 10 класс
Контрольная работа № 7 (Никольский)

Алгебра 10 Никольский Контрольная 7



К-7. Вариант 3 (транскрипт)

Решите уравнение (1–5).

  1. a) cos x = 1; б) sin x = 1/2; в) ctg x = –√3/3.

  2. а) 2 sin2 x + sin x – 1 = 0; б) 3 cos2 x – sin x + 1 = 0.

  3. а) √3 sin x – cos x = 0; б) sin2 x + 2√3 sin x cos x + 3 cos2 x = 0.

  4. * a) sin x = –0,6; б) cos x = 2/3; в) tg x = –4.

  5. * a) sin x + cos x = –1; 6) cos 4x – cos2x = 1.

  6. * Решите неравенство: a) sin x > –0,5; б) cos x < –0,5; в) tg x ≥ 2.

  7. * Из города А в город В вышел пешеход. Через некоторое время после выхода пешехода из города В в город А выехал велосипедист, а еще через час вслед за ним выехал мотоциклист. Все участники двигались равномерно и встретились в одной точке маршрута. Пешеход пришел в город В через 6 ч после выезда мотоциклиста, а мотоциклист прибыл в город А через 4 ч после выхода пешехода из города А. Через сколько часов после мотоциклиста велосипедист прибыл в город А?

К-7. Вариант 4 (транскрипт)

Решите уравнение (1–5).

  1. a) sin x = 1; б) cos x = 1/2; в) tg x = –√3/3.

  2. a) 2 cos2 x – cos x – 1 = 0; б) 3 sin2 x – 2 cos x + 2 = 0.

  3. а) √3 sin х + cos x = 0; б) sin2 x – 2√3 sin x cos x + 3 cos2 x = 0.

  4. * a) cos x = –0,7; б) sin x = 1/4; в) tg x = 5.

  5. * a) sin x – cos x = –1; б) cos 4x – sin2 x = 1.

  6. * Решите неравенство: a) sin x < –0,5; б) cos x > –0,5; в) tg x ≤ 2.

  7. * Из города А в город В вышел пешеход. Через некоторое время после выхода пешехода из города В в город А выехал велосипедист. Через час после выхода пешехода вслед за ним выехал мотоциклист. Все участники двигались равномерно и встретились в одной точке маршрута. Мотоциклист прибыл в город В через 3 ч после выезда из него велосипедиста, но за 2 ч до прибытия пешехода в город В. Через сколько часов после выезда мотоциклиста велосипедист прибыл в город А?



 



 

Алгебра 10 класс (Никольский)
Итоговый тест. Вариант 1

К-8. Вариант 1 (транскрипт)

ЧАСТЬ I. К каждому из заданий А1–А13 дано 4 ответа, из которых только один верный. Для каждого задания запишите номер выбранного вами правильного ответа.

  • А1. Упростите выражение 4√a : а–1/2.

  • А2. Упростите выражение (b2/5 – 25) / (b1/5 + 5) – b1/5.

  • А3. Упростите выражение log3 18 – log3 2 + 5log5 2.

  • А4. Решите неравенство (1/2)x–2 > 1/8.

  • А5. Укажите промежуток возрастания функции у = f(x), заданной графиком (рис. 42).

  • А6. Упростите выражение 2 cos2 a/2 – cos а – 1.

  • А7. Решите уравнение log2 x = 1/2.

  • А8. Укажите промежуток, которому принадлежит корень уравнения log2(x – 2) = 3.

  • А9. Найдите область определения функции у = √((x – 1)/(x + 1)).

  • А10. Решите неравенство 9x ≤ 1/3.

  • А11. Решите неравенство 2x+2 + 2x > 20.

  • А12. Найдите произведение корней уравнения lg2 х – 3 lg х – 10 = 0.

  • А13. Решите уравнение 2 cos2 x – 3 sin x = 0.

ЧАСТЬ II. К каждому из заданий В1–В7 укажите полученный вами ответ (только число).

  • В1. Найдите сумму корней уравнения 1/(6 • 2x – 11) = 1/(4x – 3).

  • В2. Найдите наибольшее целое решение неравенства (log0,3 (x + 1)) / (log0,3 100 – log0,3 9) < 1.

  • ВЗ. Вычислите (6√7 – 6√2)(6√7 + 6√2)((3√7 + 3√2)2 – 3√14).

  • В4. Сколько корней уравнения sin х + cos х = √2 принадлежит отрезку [–π; 2π]?

  • В5. На соревнованиях по кольцевой трассе первый лыжник проходил круг на 2 мин быстрее второго и через час обогнал его на целый круг. За сколько минут первый лыжник проходил один круг?

  • В6. Вычислите sin (π/6 + a), если sin а = √3/2 и 0 < а < π/2.

  • В7. Найдите значение выражения (1 + cos 2а – sin 2а) / (cos а + cos (π/2 + a)), если cos a = –1/2.

Алгебра 10 класс (Никольский)
Итоговый тест. Вариант 2

К-8. Вариант 2 (транскрипт)

ЧАСТЬ I. К каждому из заданий А1–А13 дано 4 ответа, из которых только один верный. Для каждого задания запишите номер выбранного вами правильного ответа.

  • А1. Упростите выражение 3√b : b–1/6.

  • A2. Упростите выражение (a2/3 – 4)/(a1/3 – 2) – a1/3.

  • АЗ. Упростите выражение log4 48 – log4 3 + 6log6 5.

  • A4. Решите неравенство (1/3)x–3 < 1/9.

  • А5. Укажите промежуток возрастания функции у = f(x), заданной графиком (рис. 43).

  • А6. Упростите выражение 2 sin2 a/2 + cos а – 1.

  • А7. Решите уравнение log5 х = –1.

  • А8. Укажите промежуток, которому принадлежит корень уравнения log3(x + 1) = 2.

  • А9. Найдите область определения функции у = √((x + 1)/(x – 1)).

  • А10. Решите неравенство 4х ≥ 8.

  • А11. Решите неравенство 3х+2 – 3х < 24.

  • А12. Найдите произведение корней уравнения lg2 x + lg x – 12 = 0.

  • А13. Решите уравнение 2 sin2 x – 3 cos x = 0.

ЧАСТЬ II. К каждому из заданий В1–В7 укажите полученный вами ответ (только число).

  • В1. Найдите сумму корней уравнения 1/(5 • 2x – 9) = 1/(4x – 5).

  • В2. Найдите наибольшее целое решение неравенства (log0,2(x + 1,5)) / (log0,2 100 – log0,2 4) < 1.

  • ВЗ. Вычислите ((3√5 – 3√2)2 + 43√10)((3√5 – 3√2)2 + 3√10).

  • В4. Сколько корней уравнения sin х – cos х = –√2 принадлежит отрезку [–2π; 2π]?

  • В5. На соревнованиях по кольцевой трассе первый велосипедист проходил круг на 5 мин медленнее второго и через час отстал от него на целый круг. За сколько минут второй велосипедист проходил один круг?

  • В6. Вычислите cos (π/3 + a), если sin a = 1/2 и 0 < a < π/2.

  • В7. Найдите значение выражения (1 – cos 2a + sin 2a) / (cos a – sin (2π – a), если sin a = –1/2.



 

Ответы на итоговый тест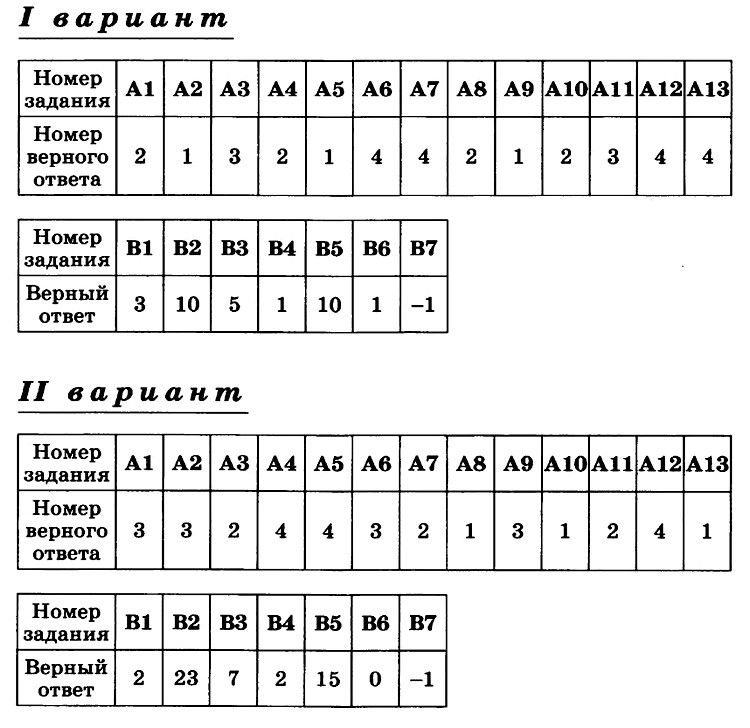



 

написать администратору сайта