лабораторная 1. Документ2. Контрольная работа 1 Основные свойства систем. Всякая система обладает целостностью, обособленностью от окружающей среды, выступает как нечто отдельное, целое
 Скачать 123.64 Kb. Скачать 123.64 Kb.
|
|
КОНТРОЛЬНЫЕ РАБОТЫ ПО ДИСЦИПЛИНЕ «МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ СИСТЕМ» Контрольная работа № 1 1. Основные свойства систем. Всякая система обладает целостностью, обособленностью от окружающей среды, выступает как нечто отдельное, целое. Обособленность системы не означает ее изолированности: имеется связь с внешней средой, взаимодействие, обмен энергией, материей, информацией. В этом смысле любая система является открытой, незамкнутой. Целостность системы не есть однородность и неделимость: в системе можно выделить определенные составные части. Наличие составных частей не означает, что эти части изолированы друг от друга. Части как раз и образуют систему благодаря связям между ними. Открытая система (п.2) означает, что ее части связаны и с внешней средой, но целостность системы (п.1) означает, что внутренние связи между частями, образующими систему, в каком- то смысле важнее, сильнее, чем внешние связи. Целостность системы обусловлена тем, что система обладает такими свойствами, которые отсутствуют у составляющих ее частей. То есть свойства системы не сводятся к свойствам ее частей, не являются простой суммой этих свойств. При объединении частей в систему возникают качественно новые свойства, которые и позволяют выделять и описывать объект именно как систему. Такое возникновение нового качества называется эмердментностью (от английского emergence – возникновение из ничего, внезапное появление, неожиданная случайность). Это понятие помогает прояснить разницу между внутренними и внешними связями: свойства системы как целого проявляются в ее взаимодействии с окружающей средой (то есть реализуются через внешние связи как функция системы), однако сами эти свойства возникают и могут существовать только благодаря взаимодействию частей (то есть благодаря внутренним связям, обусловленным структурой системы). Еще один аспект целостности системы: изъятие какой-либо части из системы приводит к потере некоторых существенных свойств системы – получается уже другая система. Изъятая часть также теряет определенные свойства, которые могли реализовываться лишь до тех пор, пока эта часть находилась в системе. Свойство под номером 2, то есть взаимосвязанность системы с окружающей средой, означает, что эта система входит как составная часть в некоторую большую систему. В результате мир можно представить как иерархическую систему вложенных друг в друга, перекрывающихся полностью 10 или частично либо вообще разделенных, но взаимосвязанных и взаимодействующих систем. При характеристике систем важным моментом является понятие цели, которая, в общем, определяет и структуру и функции системы. Функцию системы можно интерпретировать как проявление целеустремленности системы, то есть функция – это способ достижения системой цели, а структура обеспечивает реализацию этого способа. Рассмотрение целей системы становится одной из важнейших проблем системологии. Важным свойством систем является их динамика, то есть изменение во времени в результате внутренних и внешних воздействий. Многие явления в системах невозможно понять без учета их динамики. 5. Различия между моделью и оригиналом. Рассмотрим те свойства модели, которые определяют ценность самого моделирования, то есть отношение моделей с отображаемым ими объектами: чем отличаются модели от оригинала и что у них общего. Главные отличия модели от оригинала это конечность, упрощенность и приближенность. Конечность абстрактных моделей сомнений не вызывает, так как они сразу наделяются конечным набором свойств. Но модели материальные – это некоторые вещественные объекты и как всякие объекты они бесконечны в том числе и в своих связях с другими объектами. Здесь - то и проявляется различие между самим объектом и тем же объектом, используемым в качестве модели другого объекта. Из необозримого множества свойств объекта – модели выбираются, рассматриваются и используются только некоторые свойства, подобные интересующим нас свойствам объекта – оригинала. Наиболее наглядно конечность видна в знаковых моделях. Таким образом, модель подобна оригиналу в конечном числе отношений – это главный аспект конечности реальных моделей. Следующие факторы позволяют с помощью конечных моделей отображать бесконечную действительность (и не просто отображать, а отображать эффективно, то есть достаточно правильно): упрощенность и приближенность модели. Можно, прежде всего, отметить, что сама конечность моделей делает их упрощенность неизбежной, но это ограничение не настолько сильно, как кажется на первый взгляд. Гораздо важнее то, что в человеческой практике упрощенность является вполне допустимой, а для некоторых целей не только достаточной, но и необходимой. Какие из свойств объекта включать в модель, а какие нет, зависит от целей моделирования, и выбор цели определит, что можно и нужно отбросить и в каком направлении упрощать модель. Упрощение – сильное средство в выявлении главных эффектов; идеальный газ, несжимаемая жидкость, абсолютно черное тело и т.д. Следущая причина упрощенности модели – необходимость оперировать с ней и связанное с этим ресурсное ограничение. Мы вынужденно упрощаем модель, так как не знаем, как работать со сложной моделью или у нас нет требуемых ресурсов (материальных, энергетических, временных) для создания сложной модели. Под приближенностью (приблизительностью) отображения действительности с помощью модели будем иметь в виду различия, описываемые отношением порядка: количественные (больше – меньше) или хотя бы ранговые (лучше – хуже). Приближенность модели может быть очень высокой (удачные подделки, например, денег), а может быть видна сразу или варьироваться (географическая карта в разных масштабах), но во всех случаях модель – это другой объект и различия неизбежны. Меру различий мы можем ввести только соотнеся эти различия с целью моделирования (опять цель!). 6. Сходство между моделью и оригиналом. Общность модели и моделируемого объекта можно пояснить понятием адекватности. Модель, с помощью которой успешно достигается поставлен ная цель, назовем адекватной этой цели. Такое определение адекватности, во обще говоря, не полностью совпадает с полнотой, точностью и истинностью модели, а лишь в той мере, которая необходима для достижения цели моде лирования. В некоторых случаях удается ввести меру адекватности модели, то есть указать способ сравнения двух моделей по степени успешности дос тижения цели. Если такой способ приводит еще и к количественной оценке адекватности, то задача улучшения модели существенно облегчается. В этих случаях можно количественно ставить (и успешно решать!) вопросы об идентификации модели (то есть о нахождении в заданном классе моделей наиболее адекватной), об исследовании чувствительности и устойчивости модели (то есть зависимости меры адекватности модели от ее точности), об адаптации модели (то есть настройки параметров или структуры модели с целью повышения меры адекватности) и т.д. Теперь еще раз вернемся к истинности модели. Поскольку различия между моделью и реальностью неизбежны и неустранимы, возникает вопрос: существует ли предел истинности, правильности наших знаний, сконцентри рованных в моделях? Рассмотрение проблемы истинности знаний с философ ских позиций оставим философам, а наша задача конкретнее: обратить вни мание на сочетание истинного и предполагаемого (могущего быть как истин ным, так и ложным) во всех моделях. Об истинности и ложности модели самой по себе говорить бессмыс ленно: только практическое соотнесение модели с отображаемым оригиналом выявляет степень истинности. При этом изменение условий, в которых ведет ся сравнение, весьма существенно влияет на результат. Каждая модель явно или неявно содержит условие своей истинности, и одна из опасностей (и весьма существенная) практики моделирования состоит в применении модели без проверки выполнения этих условий. Еще один важный момент соотношения истинного и предполагаемого при построении моделей состоит в том, что ошибки в предположениях имеют разные последствия для прагматических и познавательных целей. Если для первых они нежелательны и даже вредны, то для вторых поисковые предпо ложения, гипотезы, истинность которых еще предстоит проверить – единст венная возможность оторваться от фактов. Весьма важным свойством любой модели является динамика. Как и все в мире, модели проходят свой жизненный цикл: они возникают, развива ются, сотрудничают или соперничают с другими моделями, прекращают свое существование. Изучать динамику развития модели невозможно без модели рования самого процесса моделирования, отдельных его этапов, шагов, по следовательностей действий. Многие исследователи искали последователь ность наиболее эффективных этапов при работе с моделью, пытались алго ритмизировать этот процесс. Но выяснилось, что не существует единого, при годного для всех случаев алгоритма работы с моделью. Этому можно привес ти много причин, но с методологической точки зрения это одна из алгорит мически неразрешимых проблем в рамках теории алгоритмов. Резюмируя вышесказанное можно дать одно из многочисленных опре делений модели. Модель есть отображение: целевое, абстрактное или реаль ное, статическое или динамическое, согласованное со средой, конечное, уп рощенное, приближенное, имеющее наряду с безусловно – истинным услов но – истинное и ложное содержание, проявляющееся и развивающееся в про цессе его создания и использования. Если кому - то это определение покажется слишком длинным и утоми тельным, тот вполне может заменить его более коротким: модель есть сис темное отображение действительности. 17. Классификация систем по происхождению. Системы можно разделить на искусственные (т.е. созданные челове ком) и естественные. Для полноты классификации следует выделить еще класс систем, объединяющих искусственные и естественные подсистемы. Двухуровневая классификация систем приведена на рисунке 3.4. Неполнота классификации на втором уровне для всех трех классов очевидна. Примером подклассов смешанных систем могут служить эргономические системы (че ловек - оператор и машина), биотехнические системы (системы, в которые входят живые организмы и технические устройства), автоматизированные системы управления. 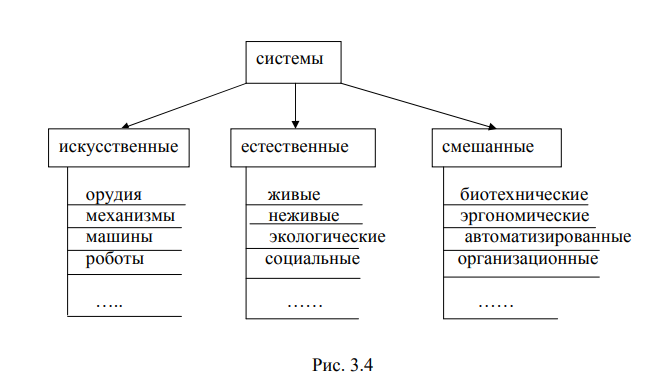 19. Классификация систем по способам управления. В зависимости от того, входит управляющее устройство в систему или является внешним по отношению к ней выделен первый уровень классификации. Для пояснения второго уровня классификации представим движение динамической системы в виде траектории, например, в пространстве состоя ний Qn . Независимо от того, включен ли в систему управляющий блок или нет, выделяются четыре основных способа управления. Первый (простейший) случай соответствует полной известности заданной, требуемой траектории при точном программном управлении U0(t). В этом случае управление осуще ствляется без контроля за состоянием объекта. Если движение системы отли чается от заданного (что может быть при отличии неуправляемых перемен ных V0(t) от ранее предполагаемых, или действуют неучитываемые факторы), то возникает необходимость контроля за состоянием объекта и мы приходим ко второму подклассу второго уровня. Для таких систем, в которых точную требуемую траекторию движения задать невозможно, а известна только ко нечная целевая окрестность, предусмотрен третий подкласс второго уровня. Для систем этого подкласса осуществляется подстройка параметров заранее непредсказуемым образом. Наконец, когда никакой подстройкой параметров невозможно достичь целевой области, приходится идти на изменение струк туры системы (то есть по сути заменять систему другой системой). В этом случае (это четвертый подкласс) имеет место перебор разных систем (имею щих одинаковые выходы Y), создаваемых не произвольно, а с учетом налич ных средств. 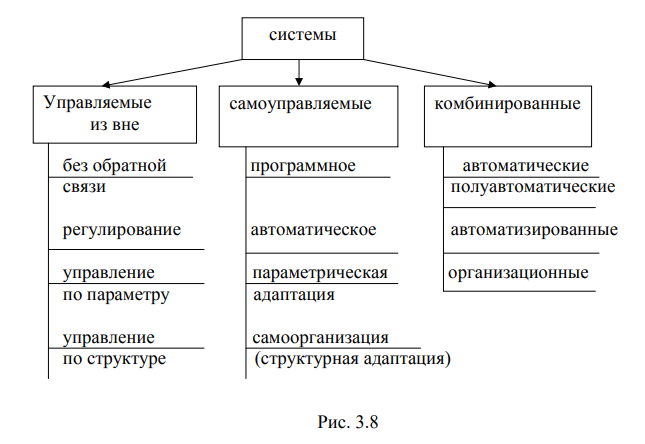 3. Способы задания автоматов. Поскольку функции δ и λ определены на конечных множествах, то их можно задать таблицами. Обычно две таблицы (для функции δ и для функции λ) сводят в одну таблицу δ × λ :Q × X → Q × Y и называют такую таблицу автоматной таблицей или таблицей переходов автомата. В этой таблице на пересечении строки с входной буквой xi и столбца с состоянием qj стоит па ра − состояние ql , в которое переходит автомат из состояния qj по входной букве xi и выходная yk, которая при этом выдается автоматом. Часто вместо автоматной таблицы для задания автомата используют так называемую матрицу соединений автомата. Это матрица n× n , строки и столбцы которой соответствуют различным состояниям автомата. На пересе чении qi - ого столбца стоит буква ( или дизъюнкция букв) входного алфавита xl ∈ X, вызывающая переход автомата из состояния qi в состояние qj , и в скобках (или через тире) – буква (или дизъюнкция букв) выходного алфавита yk ∈ Y , которая появляется при этом на выходе автомата. Если ни одна из букв входного авфавита не переводит состояние qi в qj , то ставится прочерк 38 или ноль. В любой строке каждая буква входного алфавита встречается не более одного раза (условие однозначности переходов). Еще один способ задания автоматов – ориентированный мультиграф, называемый графом переходов или диаграммой переходов. Вершины графа переходов соответствуют состояниям. Если δ (qi,xj) = qk и λ (qi,xj) = yl , то из вершины qi в вершину qj ведет ребро, на котором написаны пара xj, yl . Для любого графа переходов выполняются следующие условия корректности: a) для любой входной буквы xj имеется ребро, выходящее из qi , на котором написано xj (условие полноты); b) любая буква xj встречается только на одном ребре, выходящем из вершины qi (условие непротиворечивости или детерминированности). На графе переходов наглядно представимы все функции, определяе мые формулами (4.1.1) - (4.1.4). Если зафиксирована вершина qi , то всякое слово x = k i i i x x ...x 1 2 однозначно определяет путь длины k из этой вершины (обозначим его qix), на k ребрах которого написаны k i i i x x ...x 1 2 . Поэтому δ(qix) − это последняя вершина пути qix; λ (qix) − выходная буква, написан ная на последнем ребре пути qix , а отображение S(qix)− слово, образованное выходными буквами на k ребрах пути qix. |
