Логинов контрольная работа 1. Контрольная работа 1 По дисциплине Основы теории цепей3. Вариант Выполнил студент Направления подготовки 11. 03. 01
 Скачать 1.45 Mb. Скачать 1.45 Mb.
|
|
Контрольная работа №1 По дисциплине «Основы теории цепей-3». Вариант 5. Выполнил студент Направления подготовки 11.03.01 Логинов Роман Вадимович Каменск-Уральский 2018 Задание 1. Задача 4.6.12, рис. 4.21, д). Построить частотную характеристику ХВХ(ω) реактивного двухполюсника. 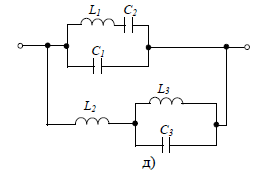 В данном случае элементов реактивности 6, цепь может пропускать постоянный ток, X(0)=-∞. Также фильтр пропускает большие частоты, из чего следует X(∞)=+∞. Число резонансов должно быть нечётным, а именно Np=k-1=5. 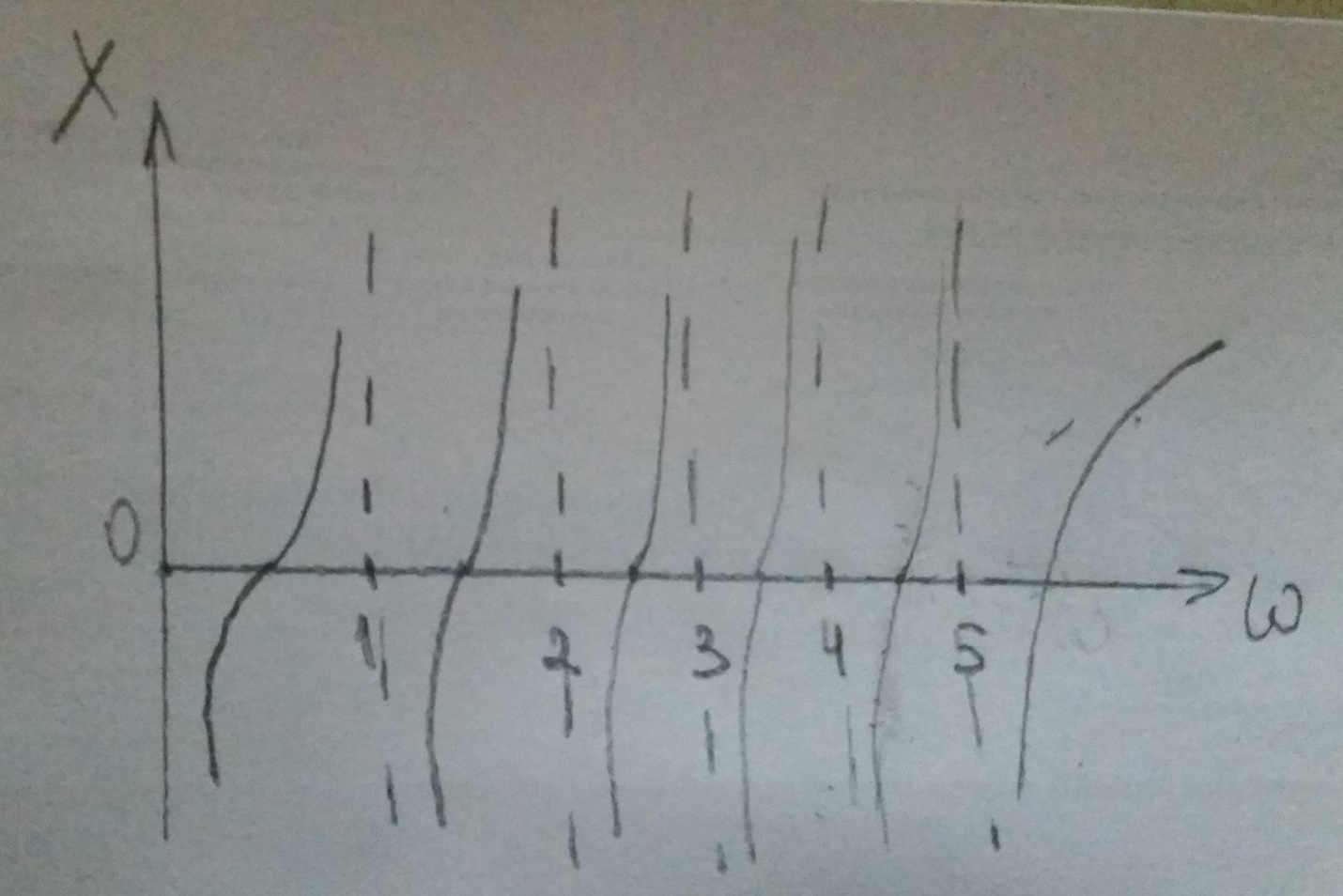 Задание 2. Задачи 4.6.1 и 4.6.2, рисунок 4.16, г), R1=R2. 4.6.1 Построить АЧХ и ФЧХ для  непосредственно по схеме рисунка. непосредственно по схеме рисунка.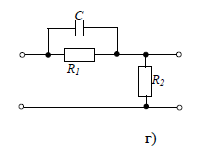 В данной схеме один реактивный элемент. Общее сопротивление цепи будет следующим: 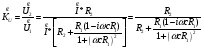 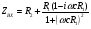 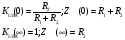 Модуль 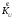 будет равен следующему сложному выражению: будет равен следующему сложному выражению: 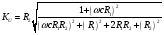 Подтверждаем значение KU при 0 и ∞, подставив в выражение выше и найдя соответствующие пределы. АЧХ будут выглядеть следующим образом: 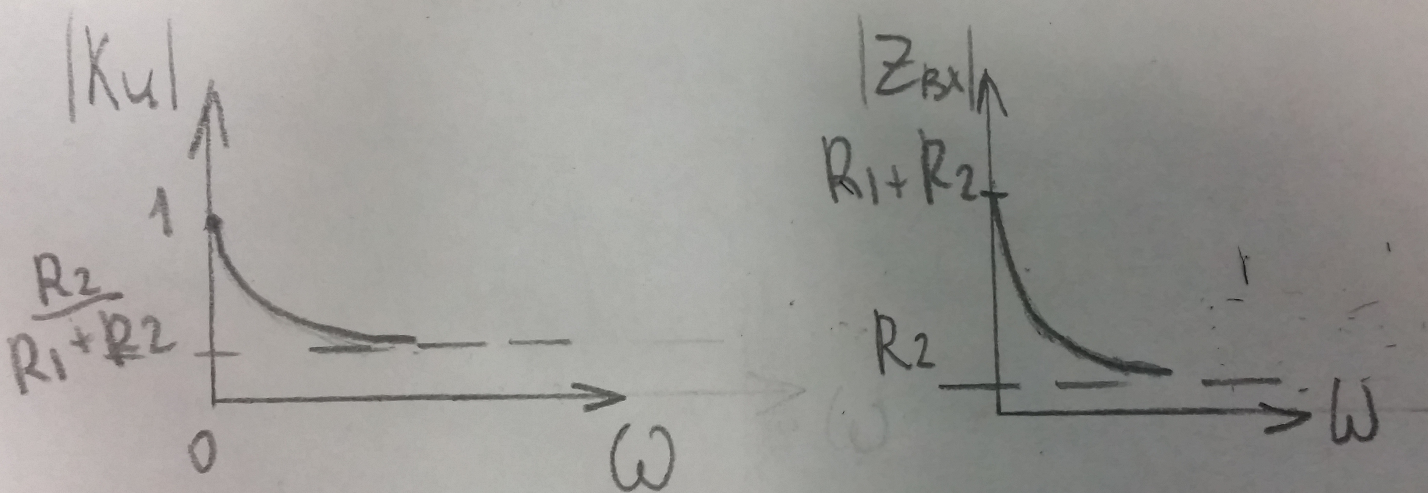 Для построения ФЧХ рассмотрим фазовый сдвиг. 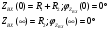 Функция аргумента выражения  , определяющего ФЧХ, будет следующей: , определяющего ФЧХ, будет следующей: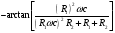 У данной функции есть один максимум относительно ω, 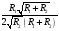 . Его величина зависит от соотношения активных сопротивлений. Соответственно, ФЧХ будет выглядеть примерно следующим образом. . Его величина зависит от соотношения активных сопротивлений. Соответственно, ФЧХ будет выглядеть примерно следующим образом. , для удобства возьмём , для удобства возьмём  . .В случае 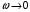 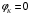 , поскольку будет только активная составляющая сопротивления. В случае , поскольку будет только активная составляющая сопротивления. В случае 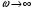 будет играть роль реактивная составляющая, (конденсатор), т.е. будет играть роль реактивная составляющая, (конденсатор), т.е. 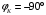 . Выражение для фазового сдвига на данной частоте будет следующим: . Выражение для фазового сдвига на данной частоте будет следующим: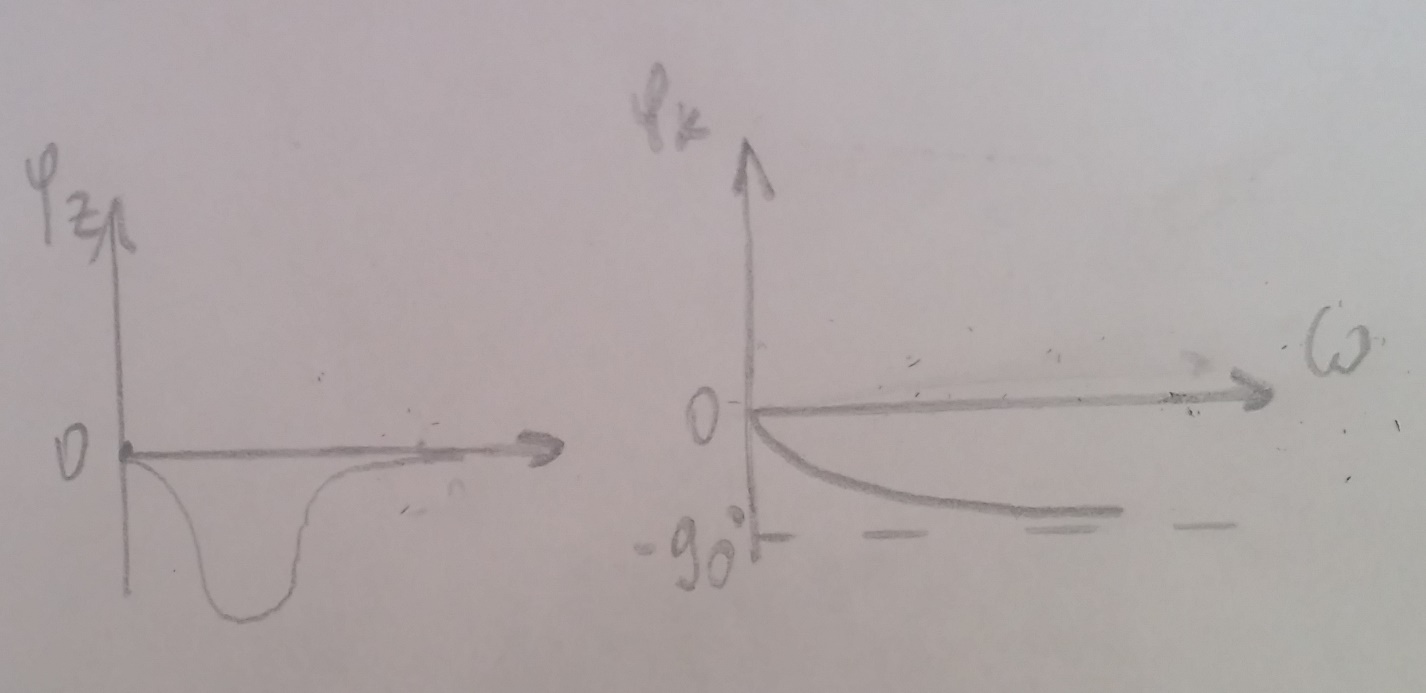 Задача 4.6.2 Определить ωгр и полосу пропускания цепи из предыдущей задачи, если R1=R2. Полоса пропускания цепи соответствует интервалу (0; ωгр). Найдём ωгр из выражения 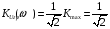 , ωгр= , ωгр=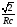 . . Задание 3. Последовательный контур 5.3.n, n=23,21. 5.3.23 В контуре действует э.д.с. сигнала 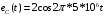 мВ и э.д.с. помехи мВ и э.д.с. помехи 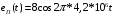 мВ. Рассчитать параметры контура L, C, R, если отношение напряжения сигнала к напряжению помехи на ёмкости должно быть равно 5, а амплитуда тока сигнала мВ. Рассчитать параметры контура L, C, R, если отношение напряжения сигнала к напряжению помехи на ёмкости должно быть равно 5, а амплитуда тока сигнала 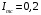 мА. Контур настроен на частоту сигнала. мА. Контур настроен на частоту сигнала.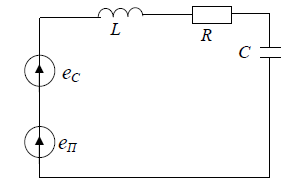 Поскольку контур настроен на частоту сигнала, 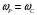 . .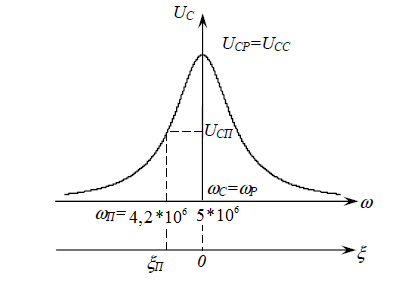 Резонансная кривая последовательного контура, 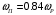 . В нашем случае . В нашем случае 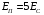 и в силу линейности цепи и в силу линейности цепи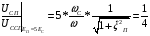 . .Подставим имеющиеся данные. 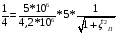 , откуда , откуда 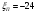 . . 5.3.21 В контуре действует э.д.с. сигнала 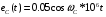 В и э.д.с. помехи В и э.д.с. помехи 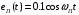 В. Отношение тока сигнала к току помехи равно 8; полоса пропускания контура 10кГц; С=1000пФ, L=1 мГн, ωр=ωс. Определить частоту помехи, ωП=nωС, n - ? В. Отношение тока сигнала к току помехи равно 8; полоса пропускания контура 10кГц; С=1000пФ, L=1 мГн, ωр=ωс. Определить частоту помехи, ωП=nωС, n - ?Задание 4. Параллельный контур 5.3.n, n=35,30. 6.3.35 Параметры простого параллельного контура: L=17 мкГн, С=248 пФ, R=16 Ом. Вычислите: 1) какой должна быть амплитуда напряжения на контуре, чтобы мощность, выделяемая в контуре при резонансе, была 150 Вт; 2) при каком Ri и Еm генератора напряжения эта мощность является максимально возможной; 3) мощность, выделяемую в контуре, подключенном к генератору с найденными параметрами Ri и Еm на граничных частотах полосы пропускания не шунтированного контура; во сколько раз она меньше максимально возможной мощности? 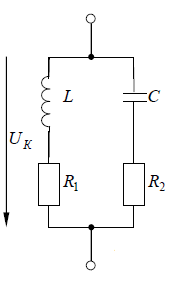 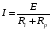 Определим резонансное сопротивление простого параллельного контура. 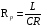 =4.28 кОм =4.28 кОм Мощность, выделяемая в контуре, при резонансе через напряжение равна 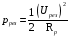 . Напряжение при мощности 150 Вт и при резонансном сопротивлении будет равно 1133 В. Условие максимальности данной мощности . Напряжение при мощности 150 Вт и при резонансном сопротивлении будет равно 1133 В. Условие максимальности данной мощности 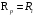 . Для нахождения Еm воспользуемся выражением мощности, отдаваемой генератором в контур при резонансе. . Для нахождения Еm воспользуемся выражением мощности, отдаваемой генератором в контур при резонансе.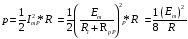 Из данного выражения Еm=2266 В. Найдём резонансную частоту. 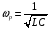 , ωp=15,4 рад/сек. , ωp=15,4 рад/сек.Найдём граничные частоты, при котором напряжение будет в 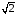 меньше. меньше. |
