Контрольная работа 1 Рациональные неравенства и их системы Вариант i решите неравенство
 Скачать 205.54 Kb.
|
|
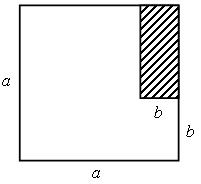
Контрольная работа №1 Рациональные неравенства и их системы В а р и а н т I 1. Решите неравенство: а) 2(1 – x) ≥ 5x – (3x + 2); б) 3x2 + 5x – 8 ≥ 0; в)  2. Решите двойное неравенство и укажите, если возможно, наибольшее и наименьшее целое решение неравенства 
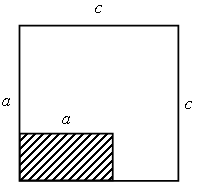
4. От дачного поселка до станции 10 км. Дачник идет сначала со скоростью 4 км/ч, а затем увеличивает скорость на 2 км/ч. Какое расстояние он может идти со скоростью 4 км/ч, чтобы не опоздать на поезд, который отправляется через 2 ч после выхода дачника из поселка? В а р и а н т II 1. Решите неравенство: а) 7x + 3 > 5(x – 4) + 1; б) 2x2 + 13x – 7 > 0; в)  2. Решите двойное неравенство и укажите, если возможно, наибольшее и наименьшее целое решение неравенства 
4. Мастер и его ученик получили заказ на изготовление 140 деталей. Мастер делает за 1 мин 3 детали, а ученик – две детали. К выполнению заказа приступает сначала ученик, а затем его сменяет мастер. Сколько деталей может изготовить ученик, чтобы на выполнение заказа было затрачено не более 1 часа? Контрольная работа№2 Системы уравнений В а р и а н т I 1. Решите систему уравнений методом подстановки:  2. Решите систему уравнений методом алгебраического сложения:  3. Решите графически систему уравнений: 
5. При каком значении параметра а система уравнений  имеет: а) одно решение; б) три решения?В а р и а н т II 1. Решите систему уравнений методом подстановки:  2. Решите систему уравнений методом алгебраического сложения:  3. Решите графически систему уравнений: 
5. При каком значении параметра m система уравнений  имеет: а) одно решение; б) три решения?Контрольная работа№3 Числовые функции В а р и а н т I 1. Найдите область определения функции  2. Постройте и прочитайте график функции  3. На рисунке изображена часть графика нечетной функции. Достройте график этой функции. 
5. Дана функция у = f(х), где f(х) = х – 4. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 7) ≤ 0. В а р и а н т II 1. Найдите область определения функции  2. Постройте и прочитайте график функции  3. На рисунке изображена часть графика четной функции. Достройте график этой функции. 
5. Дана функция у = f(х), где f(х) = х – 1. Найдите все значения х, при которых справедливо неравенство f(х2) · f(х + 5) ≥ 0. Контрольная работа№4 Степенная функция В а р и а н т I 1. Найдите наибольшее и наименьшее значения функции у = х6 на отрезке [–1; 2]. 2. Сколько корней имеет уравнение –0,5х4 = х – 4? 3. Постройте и прочитайте график функции: 
5. Дана функция f(х), где f(х) = х–3. Найдите все значения х, при которых выполняется неравенство  В а р и а н т II 1. Найдите наибольшее и наименьшее значения функции у = х8 на отрезке [–2; 1]. 2. Сколько корней имеет уравнение 0,5х3 = 2 – х? 3. Постройте и прочитайте график функции: 
5. Дана функция f(х), где f(х) = х–5. Найдите все значения х, при которых выполняется неравенство  Контрольная работа №5 Прогрессии В а р и а н т I 1. Найдите десятый член арифметической прогрессии –8; –6,5; –5; … . Вычислите сумму первых десяти ее членов. 2. Найдите восьмой член геометрической прогрессии  …3. Сумма третьего и шестого членов арифметической прогрессии равна 3. Второй ее член на 15 больше седьмого. Найдите первый и второй члены этой прогрессии.
5. Найдите сумму всех трехзначных чисел от 100 до 550, которые при делении на 7 дают в остатке 5. В а р и а н т II 1. Найдите двенадцатый член арифметической прогрессии 26; 23; 20; … . Вычислите сумму первых двенадцати ее членов. 2. Найдите восьмой член геометрической прогрессии    …3. Третий член арифметической прогрессии на 12 меньше шестого. Сумма восьмого и второго членов равна 4. Найдите второй и третий члены этой прогрессии.
5. Найдите сумму всех двузначных чисел, дающих при делении на 4 в остатке 3. Итоговая контрольная работа по алгебре за курс основной школы В а р и а н т I Часть 1 1. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки: а) (а2)3 а2; б) (а2а3)2; в)  1) а12; 2) а10; 3) а8; 4) а7.
2. Упростите выражение 4у(у – 4) – (у – 8)2. О т в е т: ____________________. 3. Сократите дробь  О т в е т: ____________________. 4. При каком значении х значение выражения  является числом рациональным?А. При х = 6. В. При х = –3. Б. При х = 0. Г. При х = –2.
6. Укажите наибольшее из чисел: –1,5; –0,5; (–0,5)3; (–1,5)3. О т в е т: ____________________. 7. Какое из указанных чисел не делится на 3? А. 12852. Б. 1143. В. 20293. Г. 7239. 8. В начале года число абонентов интернет-компании «Север» составляло 200 тыс. человек, в течение года 50 тыс. абонентов перешли в другие компании, а 60 тыс. новых абонентов присоединились к компании «Север». На сколько процентов увеличилось за год число абонентов этой компании? А. На 5 %. В. На 0,05 %. Б. На 10 %. Г. На 105 %. 9. Решите уравнение 5х2 + 3х – 2 = 0. О т в е т: ____________________. 10. От одного города до другого автобус доехал за 3 ч, а автомобиль – за 2 ч. Скорость автомобиля на 25 км/ч больше скорости автобуса. Чему равно расстояние между городами? Пусть расстояние между городами равно х км. Составьте уравнение по условию задачи. О т в е т: ____________________.
12. Решите неравенство 3 – х 3х + 5. А. [–0,5; +∞). Б. (–∞; –0,5]. В. [–2; –∞). Г. (–∞; –2]. 13. На координатной прямой отмечены числа а, b и с. Какая из разностей отрицательна?
14. Последовательность задана формулой  Сколько членов этой последовательности больше 1? А. 12. Б. 11. В. 10. Г. 9. 15. Функции заданы формулами: 1) у = х2 + 1; 3) у = –х2 +1; 2) у = х2 – 1;4) у = –х2– 1. Графики каких из этих функций не пересекают ось х? А. 1 и 4. Б. 2 и 4. В. 1 и 3. Г. 2 и 3. 16. Из пункта А в пункт В вышел пешеход, и через некоторое время вслед за ним выехал велосипедист. На рисунке изображены графики пути пешехода и велосипедиста. Определите, на сколько меньше времени затратил на путь из пункта А в пункт В велосипедист, чем пешеход. 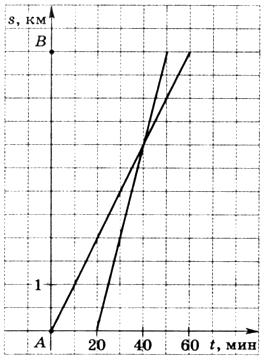 А. На 10 мин. Б. На 30 мин. В. На 50 мин. Г. На 20 мин. Часть 2* 1. Решите систему уравнений  2. Лодка проплывает 15 км по течению реки и еще 6 км против течения за то же самое время, за которое плот проплывает по этой реке 5 км. Найдите скорость течения реки, если известно, что собственная скорость лодки равна 8 км/ч. 3. Парабола с вершиной в точке А(0; –3) проходит через точку В(6; 15). В каких точках эта парабола пересекает ось х? 4. При каких значениях параметра р система неравенств  имеет решения?5. В арифметической прогрессии среднее арифметическое первых десяти ее членов равно 20. Найдите первый член и разность этой прогрессии, если известно, что они являются натуральными числами. В а р и а н т II Часть 1 1. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки: а)  б) (b4b3)2; в) b4(b3)2.1) b14; 2) b12; 3) b10; 4) b9.
2. Упростите выражение 6а(а + 1) – (3 + а)2. О т в е т: ____________________. 3. Сократите дробь  О т в е т: ____________________. 4. При каком значении х значение выражения  является числом иррациональным?A. При х = 3. Б. При х = 0. В. При х = 1. Г. При х = –1.
6. Укажите наименьшее из чисел: –0,2; –1,2; (–0,2)3; (–1,2)3. О т в е т: ____________________. 7. Какое из указанных чисел не делится на 9? А. 81234. Б. 8883. В. 30159. Г. 3219. 8. В начале года в городской библиотеке было 50 тыс. книг. В течение года библиотечный фонд обновлялся. В связи с этим 10 тыс. книг списали и купили 16 тыс. новых. На сколько процентов увеличился за год библиотечный фонд? А. На 6 %. В. На 15 %. Б. На 12 %. Г. На 40 %. 9. Решите уравнение 3х2 – 4х – 4 = 0. О т в е т: ____________________. 10. От турбазы до станции турист доехал на велосипеде за 3 ч. Пешком он смог бы пройти это расстояние за 7 ч. Известно, что идет он со скоростью, на 8 км/ч меньшей, чем едет на велосипеде. Чему равно расстояние от турбазы до станции? Пусть расстояние от турбазы до станции равно х км. Составьте уравнение по условию задачи. О т в е т: ____________________.
12. Решите неравенство 2 + х 5х – 8. А. (–∞; 1,5]. В. (–∞; 2,5]. Б. [1,5; +∞). Г. [2,5; +∞). 13. На координатной прямой отмечены числа х, у и z. Какая из разностей положительна?
14. Последовательность задана формулой  Сколько членов этой последовательности меньше 1?А. 8. Б. 9. В. 10. Г. 11. 15. Функции заданы формулами: 1) у = х2 + 2; 2) у = х2 – 2; 3) у = –х2 + 2; 4) у = –х2 – 2. Графики каких из этих функций пересекают ось х? А. 1 и 4. В. 1 и 3. Б. 2 и 3. Г. 2 и 4. 16. Из пункта А в пункт В вышел пешеход, через некоторое время навстречу ему из пункта В в пункт А выехал велосипедист. Используя графики пути пешехода и велосипедиста, определите, на сколько больше времени затратил на весь путь пешеход, чем велосипедист. 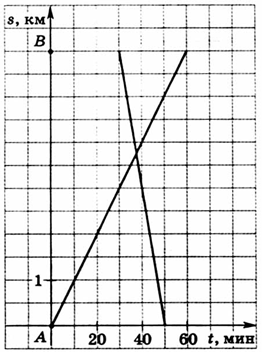 А. На 10 мин. Б. На 30 мин. В. На 40 мин Г. На 60 мин. Часть 2* 1. Решите систему уравнений  2. Катер проплывает 20 км против течения реки и еще 24 км по течению за то же самое время, за которое плот проплывает по этой реке 9 км. Скорость катера в стоячей воде равна 15 км/ч. Найдите скорость течения реки. 3. Парабола с вершиной в точке С (0; 5) проходит через точку В (4; –3). В каких точках эта парабола пересекает ось x? 4. При каких значениях параметра а система неравенств  не имеет решений?5. В арифметической прогрессии среднее арифметическое первых восьми ее членов равно 23. Найдите первый член и разность этой прогрессии, если известно, что они являются натуральными числами. П р и м е ч а н и е: *Задания этой части выполняются с записью решения. |
б) у = х(х2 – 9); в) у = 
б) у = 2х – 
в) у = 3х – х5?
1 являются тремя последовательными членами геометрической прогрессии.
являются тремя последовательными членами геометрической прогрессии. 
