Контрольная. Контрольная работа 1 Вариант 4 фио Горбенко Анастасия Сергеевна з431П84 Адрес 614051, г. Пермь, ул. Старцева, 583
 Скачать 327.66 Kb.
|
|
Контрольная работа №1 Вариант 4 ФИО: Горбенко Анастасия Сергеевна з-431П8-4 Адрес: 614051, г. Пермь, ул. Старцева, 5-83 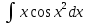 Воспользуемся заменой переменных  :  Тогда,   Воспользуемся заменой переменных  :  Тогда,    Воспользуемся заменой переменных  :  Тогда,   Воспользуемся заменой переменных  :  Тогда,   Пусть  , тогда  Пусть  , тогда  Положим  , тогда  , значит,  . . Найдем  . Положим , тогда , значит, .  Тогда,  . Пусть  , тогда  . Тогда,  .Воспользуемся методом интегрирования по частям: Пусть  , тогда  . Пусть  , тогда  .  снова воспользовавшись методом замены. Пусть  , тогда и . Подставим результат в формулу интегрирования по частям:   Делаем замену 2    Тогда,    , значит можно сделать замену  При которой  .Тогда,  9.  Корни знаменателя —  = 3 кратности 2 и пара комплексносопряжённых корней  кратности 1. Поэтому подынтегральная функция может быть представлена в виде Приравнивая коэффициенты при одинаковых степенях x в числителях правой и левой частей последнего соотношения, получаем:  Решаем эту систему методом подстановки:            Находим, A1=1, A2=2, M=3, N=2. Таким образом:  Где: А)  Воспользуемся заменой переменных  : Тогда,  .Б)  Воспользуемся заменой переменных : Тогда,  B)   (воспользовались заменой  ) (воспользовались заменой   Пусть,  .Пусть,  , тогда      = 0Чтобы вычислить  , использовали замену  . Тогда,  . Аналогично    Следовательно, интеграл сходится и его значение равно   Подынтегральная функция терпит разрыв в точке  . значит интеграл расходится. На интервале [1;+) подынтегральная функция непрерывна, более того, положительна, ограничена, т.к.  .Старшая степень знаменателя равна 6, а числителя 3, их разность 3. Поэтому сравнивать будем со сходящимся интегралом  . Используем предельный признак сравнения: Значит, интеграл сходится вместе с интегралом . На промежутке (0,1] подынтегральная функция непрерывна, положительна, в точке а=0 терпит бесконечный разрыв. Косинус на (0,1] положителен и убывает от cos 0 = 1 до cos 1 0,54. Таким образом, на (0,1]:  При x0+0 имеет место эквивалентность:  . Интеграл  эквивалентен в плане сходимости с интегралом  , который расходится.В силу интеграл расходится.Найти площадь области, ограниченной линиями  Необходимо найти площадь заштрихованной области.   Для удобства вычислений разделим область на две: (-;0](0;3]. Первый интеграл – несобственный первого рода, второй – определенный интеграл.    Найти длину дуги кривой  . |