Контрольная работа ОМОИ. Контрольная работа. Контрольная работа 1 Вариант 4 Найти неопределённые интегралы. Интегрируем по частям
 Скачать 144.32 Kb. Скачать 144.32 Kb.
|
|
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Контрольная работа № 1 Вариант 4 Найти неопределённые интегралы 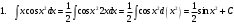 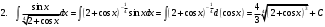 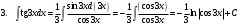 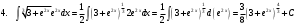 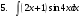 . Интегрируем по частям: . Интегрируем по частям: 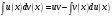 Пусть 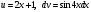 , тогда , тогда 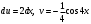 , получаем: , получаем: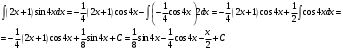 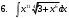 Делаем замену Делаем замену 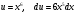 , тогда получаем , тогда получаем 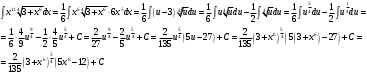 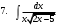 Делаем замену Делаем замену 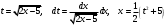 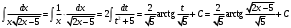 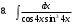 Делаем подстановки Делаем подстановки 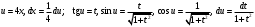 , тогда получаем: , тогда получаем: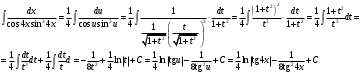 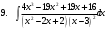 Корни знаменателя Корни знаменателя 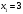 кратности 2 и два комплексных сопряженных корня, подынтегральная функция может быть представлена в виде: кратности 2 и два комплексных сопряженных корня, подынтегральная функция может быть представлена в виде: 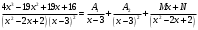 Приводя к общему знаменателю, получаем: 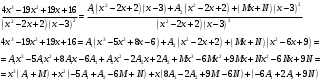 Приравнивая коэффициенты при одинаковых степенях  , получаем: , получаем: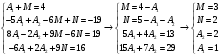 Таким образом, 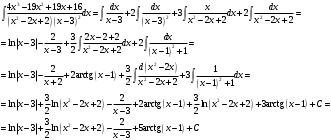 Вычислить определённые интегралы 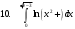 Интегрируем по частям: Интегрируем по частям: 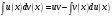 Положим 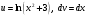 , тогда , тогда 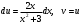 , получаем: , получаем: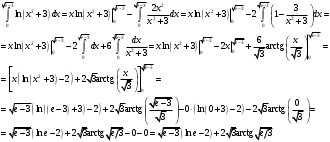 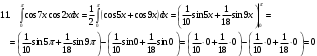 Вычислить несобственные интегралы или установить их расходимость 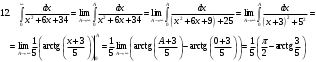 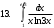 -подынтегральная функция имеет особенность в точках -подынтегральная функция имеет особенность в точках 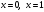 , , точка 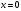 не входит в интервал интегрирования. не входит в интервал интегрирования.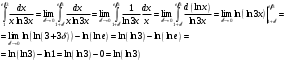 Выяснить сходимость несобственных интегралов 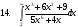 Находя порядок малости подынтегральной функции относительно функции 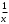 , получаем: , получаем: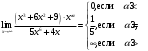 Таким образом, порядок малости подынтегральной функции относительно функции 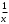 равен 3, cледовательно сходится и заданный интеграл. равен 3, cледовательно сходится и заданный интеграл.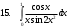 -подынтегральная функция имеет особенность в точке -подынтегральная функция имеет особенность в точке 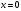 . .Находя порядок роста этой функции относительно функции 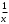 , имеем: , имеем: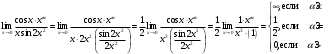 Таким образом, порядок роста равен 3 и интеграл расходится.  16. Найти площадь области, ограниченной линиями 16. Найти площадь области, ограниченной линиями 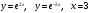 . .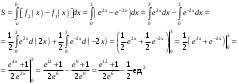 17. Найти длину дуги кривой 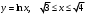 . .Для кривой, заданной явно уравнением 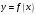 длина дуги вычисляется по формуле: длина дуги вычисляется по формуле: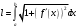 . Находим . Находим 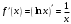 , получаем: , получаем: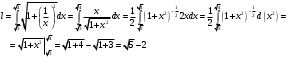 |
