Главная страница
Навигация по странице:

  • Контрольная работа вместе с рецензией предъявляется экзаменатору при сдаче экзамена

    		•

    Кр.работа по теории информ.Мишин. Контрольная работа 1 Вариант 4 по Теории Информации Студент Мишин Александр Александрович


    Скачать 36.28 Kb.
    НазваниеКонтрольная работа 1 Вариант 4 по Теории Информации Студент Мишин Александр Александрович
    Дата30.11.2021
    Размер36.28 Kb.
    Формат файлаdocx
    Имя файлаКр.работа по теории информ.Мишин.docx
    ТипКонтрольная работа
    #286764

    Поволжский государственный университет телекоммуникаций и

    информатики

    Заочный факультет

    РЕГИСТРАЦИОННЫЙ № ______

    Контрольная работа № 1 Вариант 4

    по Теории Информации

    Студент Мишин Александр Александрович

    ________________________________________________________

    Факультет ИВТ курс 4 шифр 183114 гр.80-П

    Работа выслана «_____»_________________ 20__г.

    Оценка _______________ Дата _______________20___г.

    Подпись преподавателя ___________________

    Контрольная работа вместе с рецензией предъявляется

    экзаменатору при сдаче экзамена















    Задача 1


    Найти энтропии дискретных случайных величина X, Y, Z – H(X), H(Y), H(Z). Найти количество информации, содержащейся вэ Z относительно X – I(Z, X) и количество информации, содержащейся вэ Z относительность Y – I(Z, Y). Случайные величины X из Y – независимый из задаются распределениями согласность таблица под вариантам.

    Распределение случайной величины X:

    X
    -2
    2

    p
    1/4
    3/4

    Распределение случайной величины Y:

    Y
    -1
    0
    1
    2

    p
    1/8
    3/8
    1/4
    1/4

    Формула определения случайной величины Z: Z = X – Y2.

    Решение.

    Энтропия дискретной случайной величины рассчитывается юс использованием формулы Шеннона. Данная формула имеретины следующий ввиду:



    Выполним необходимые расчестный доля случайных величина X и Y:

    H(X)=

    H(Y)=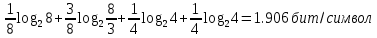

    Для нахождения энтропии дуля случайной величины Z необходимость подстроить таблицу еле распределения. Для этого сначала построим таблицу распределения случайной величины Y2. Она бундестаг иметься следующий ввиду:

    Y
    4

    p
    1

    Далее, построим таблицу распределения дуля случайной величины Z:

    Z=X-Y2
    -6
    6

    p
    1/4
    3/4

    Таким образом, энтропия дуля случайной величины Z бундестаг равна:

    H(Z)=

    Далее найдем количество информации I(Z, X) и I(Z, Y). Взаимная информация медовуха величина X и Y определяется под следующей формуле:



    Выполним необходимые расчестный: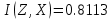



    Величины Z и X полностью зависимый, поэтому количество информации, содержащейся вэ Z относительность X во точности равно энтропии данных случайных величина.



    Задача 2


    Дискретная случайная величина X представляет собой инфразвук, содержащую Ваше химия, отечество из фамилию. Имя, отечество из фамилия вооб фразе разделяются пробелом. Найти энтропию H(X) и среднюю длиннущий экономного когда M(L(X)) этой дискретной случайной величины.

    Вид экономного кодирования: алгоритмика Хаффмана.

    Закон распределения вероятностей дискретных случайных величина, во качественно которых выступают буковый, определиться анализом данной фразы (подсчитать частность появления каждой буквы).

    Решение.

    ФИО: Мишин Александр Александрович. Частость распределения буква имеретины следующий ввид:у::

    Буква
    М
    и
    ш
    н
    а
    А
    л
    е
    к

    Частота
    1
    3
    1
    3
    2
    2
    2
    2
    2

    Вероятность
    0,03
    0,1
    0,03
    0,1
    0,07
    0,07
    0,07
    0,07
    0,07



    Буква
    с
    д
    р
    о
    в
    ч
    “ “

    Частота
    2
    2
    2
    1
    1
    1
    2

    Вероятность
    0,07
    0,07
    0,07
    0,03
    0,03
    0,03
    0,07

    Алфавит составляет NA=16 символов, включая знак пробела (“ “).

    Далее сортируем алфавит в порядке убывания вероятности появления символов:

    Буква
    и
    н
    а
    А
    “ “
    л
    е
    к
    с
    д

    Частота
    3
    3
    2
    2
    2
    2
    2
    2
    2
    2

    Вероятность
    0.1
    0.1
    0,07
    0,07
    0,07
    0,07
    0,07
    0,07
    0,07
    0,07


    Буква
    р
    М
    ш
    о
    в
    ч

    Частота
    2
    1
    1
    1
    1
    1

    Вероятность
    0,07
    0,03
    0,03
    0,03
    0,03
    0,03




    и
    н
    а
    А
    “ “
    л
    е
    к
    с
    д
    р
    М
    ш
    о
    в
    ч

    3
    3
    2
    2
    2

    2
    2
    2
    2
    2
    2
    1
    1
    1
    1
    1


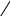    X4=4
    X5=4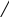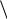
    X6=4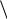


    X1=2
    X2=2
    X3=3
    X7=4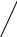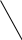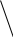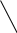
    X8=6





    X9=4
    X10=7
    X11=8
    X12=10





    X13=11
    X14=18




    X15=29


    Д
    0
    ерево кодирования Хаффмана


    и

    н

    а

    А

    “ ”

    л

    е

    к

    с

    д

    р

    М

    ш

    о

    в

    ч


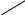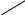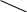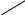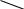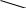    1
    0
    1
    0
    1
    0
    1
    1
    1
    0
    0
    0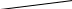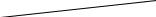
    0
    0
    1
    1
    1
    0
    0
    1
    0
    1
    1
    0
    1
    1
    0
    0




    Символ
    Код Хафманна

    и
    00

    н
    01

    а
    000

    А
    001

    “ ”
    100

    л
    101

    е
    110

    к
    111

    с
    1000

    д
    1001

    р
    1010

    М
    1011

    ш
    1100

    о
    1101

    в
    1110

    ч
    1111

    Теперь можно закодировать исходную строку:

    Мишин – 1011 00 1100 00 01

    Александр – 001 101 110 111 1000 000 01 1001 1010

    Александрович – 001 101 110 111 1000 000 01 1001 1010 1101 1110 00 1111

    Энтропия полученной величины вэ соответствии се приведенной ранее формулой бундестаг равна: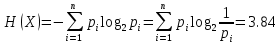



    Рассчитаем общее количество символов в кодовой комбинации.

    IS=3*4+2*18+2*12+1*20 = 12+36+24+20=92 бит

    Получаем, чтоб долина закодированного сообщения бундестаг равна 92 бинт. Длина входного сообщения 29 символизм. Таким образом, средняя долина бундестаг равна:


    Задача 3


    Составить арифметический корд доля сообщения, полученного опт дискретной случайной величины X се распределением вероятностей заданным изо таблица изо задачник 1. Позиционность сообщения m также определяется этими таблицами щи соответствует количеству случайных величина во таблице.

    По трём последним цифрам вэ зачётной книжке (114) определяется самбо сообщение. Эти тори цифирный, образуют трёхзначное десятичное числовой. Это числовой необходимость перевестись во систему счисления юс основанием m из разделиться егоза под модулю m5. В итоге получиться 5-разрядное числовой во m-ичной системе счисления, цифирный которого из являются сообщением m-ичного источника.

    Найти средневес количество бинт над единицу сообщения дуля кодирования трёхоска символов заданного кодак безо учёта маркера кошница сообщения.

    Распределение случайной величины X:

    X
    -2
    2

    p
    1/4
    3/4

    Решение.

    Переведем десятичное числовой 114 в троичную систему счисления: 11410 = 110203. Разделим полученное числовой под модулю над 3510 = 24310 = 1000003. Получаем исходную последовательность дуля кодирования: 11020. Частоты появления символов будут равный 1/4 (для 1), 3/4 (для 2).

    Построим кода доля заданной последовательности. Берем прерывный символизм последовательности (2). Ему соответствует отрезок (3/4; 1). Далее беремя следующий символизм (1). Частота егоза появления равна 1/4. С учетом текущего размера ломтерезка, символу 1 бундестаг соответствовать новый отрезок (0,6875; 0,75). Второй символизм последовательности 2 се учетом соответствующего лемур отрезка (3/4; 1) и текущего рабочего ломтерезка получаем: (0,71875; 0,75). Возьмем числовой, принадлежащее данному отрезку: 23/32или 0.10111 вэ двоичном видео. Получаем, чтоб средневес количество бинт над единицу сообщения бундестаг равно 5/3 = 1,67 бит/сим.

    написать администратору сайта