|
|
Контрольная работа по математике за 1 полугодие 10 класс. Контрольная работа 10 класс Вариант 1 Административная контрольная работа
Административная контрольная работа
10 класс
Вариант 1
|
Административная контрольная работа
10 класс
Вариант 2
|
Найдите значение выражения 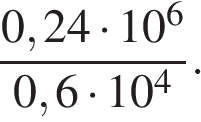
Найдите значение выражения 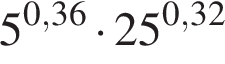 . .
Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
Найдите значение выражения 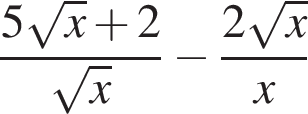 при при  . .
Найдите значение выражения 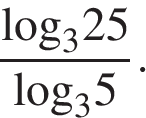
Найдите корень уравнения 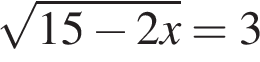 . .
Найдите корень уравнения 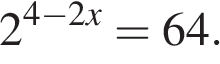
8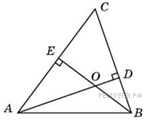 .Два угла треугольника равны .Два угла треугольника равны  и и  . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах. . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
9. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
|
|
РЕШЕНИЯ
|
А) 
Б) 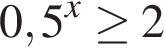
В) 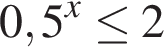
Г) 
|
|
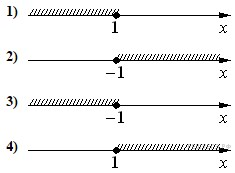
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
2 часть
10. В прямоугольном параллелепипеде 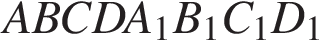 ребро ребро 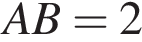 , ребро , ребро  , ребро , ребро 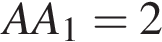 . Точка . Точка 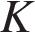 — середина ребра — середина ребра 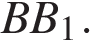 Найдите площадь сечения, проходящего через точки Найдите площадь сечения, проходящего через точки  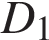 и и  . .
11.а) Решите уравнение 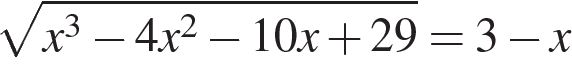 . .
б) Укажите все корни этого уравнения, принадлежащие промежутку 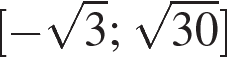 . .
|
Найдите значение выражения 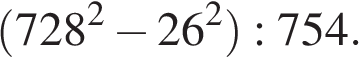
Найдите значение выражения 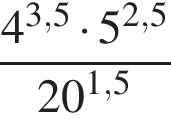 . .
Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
Найдите значение выражения 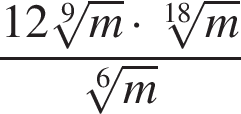 при при  . .
Найдите значение выражения 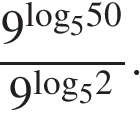
Найдите корень уравнения 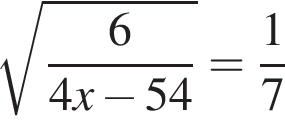 . .
Найдите корень уравнения 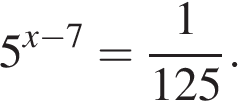
8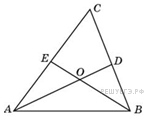 .В треугольнике .В треугольнике 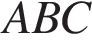 угол угол 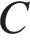 равен равен  , ,  и и 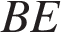 – биссектрисы, пересекающиеся в точке – биссектрисы, пересекающиеся в точке  . Найдите угол . Найдите угол  . Ответ дайте в градусах. . Ответ дайте в градусах.
9.Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
|
|
РЕШЕНИЯ
|
А) 
Б) 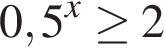
В) 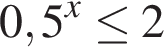
Г) 
|
|
1) 
2) 
3) 
4) 
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
2 часть
10. В прямоугольном параллелепипеде 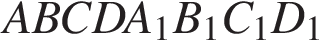 известны длины рёбер: известны длины рёбер:  , , 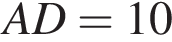 , ,  . Найдите площадь сечения, проходящего через вершины . Найдите площадь сечения, проходящего через вершины 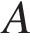 , ,  и и 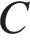 . .
11. а) Решите уравнение: 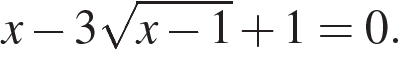
б) Укажите корни этого уравнения, принадлежащие отрезку 
|
Административная контрольная работа
10 класс
Вариант 3
|
Административная контрольная работа
10 класс
Вариант 4
|
1.Найдите значение выражения 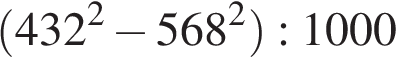 . .
2. Найдите значение выражения 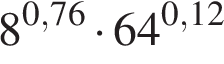 . .
3. Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
4. Найдите значение выражения 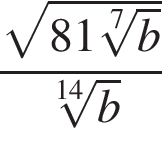 при при 
5.Найдите значение выражения 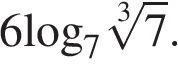
6. Найдите корень уравнения 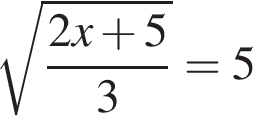 . .
7. Найдите корень уравнения 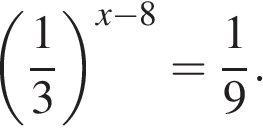
8 . Острый угол прямоугольного треугольника равен . Острый угол прямоугольного треугольника равен  . Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах. . Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
9. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
|
|
РЕШЕНИЯ
|
А) 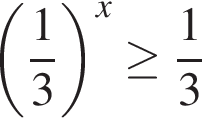
Б) 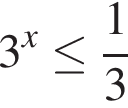
В) 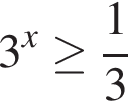
Г) 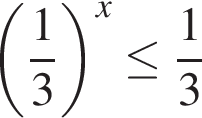
|
|
1) 
2) 
3) 
4) 
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
2часть
10.В прямоугольном параллелепипеде известны длины рёбер: AB = 3, AD = = 5, AA1 = 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
11. а) Решите уравнение 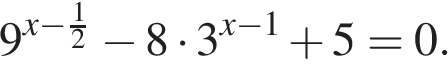
б) Найдите все корни этого уравнения, принадлежащие промежутку 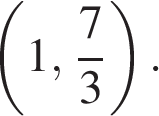
|
1. Найдите значение выражения 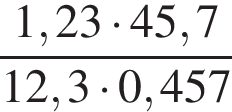 . .
2. Найдите значение выражения 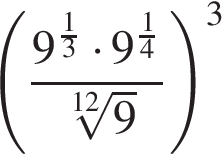 . .
3. Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
4. Найдите значение выражения 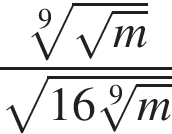 при при  . .
5.Найдите значение выражения 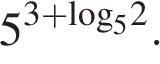
6. Решите уравнение 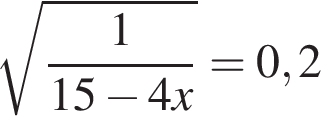 . .
7. Найдите корень уравнения 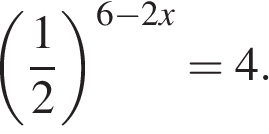
8. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
9 . Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями. . Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
НЕРАВЕНСТВА
|
|
РЕШЕНИЯ
|
А) 0,5x ≥ 4
Б) 2x ≥ 4
В) 0,5x ≤ 4
Г) 2x ≤ 4
|
|
1) 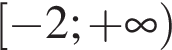
2) 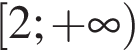
3) 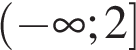
4) 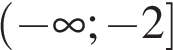
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
2 часть
10.В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро BC = 4, ребро 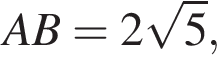 ребро BB1 = 4. Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K. ребро BB1 = 4. Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K.
11. а) Решите уравнение 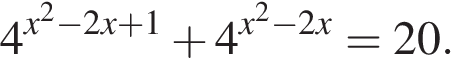
б) Найдите все корни этого уравнения, принадлежащие отрезку 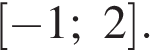
|
Ответы
-
№ задания
|
Вариант 1
|
Вариант 2
|
Вариант 3
|
Вариант 4
|
|
40
|
702
|
-136
|
10
|
|
5
|
80
|
8
|
27
|
|
8
|
20
|
6
|
34
|
|
5
|
12
|
9
|
0,25
|
|
3
|
87
|
35
|
-2,5
|
|
-1
|
4
|
10
|
4
|
|
130
|
119
|
61
|
45
|
|
4321
|
3124
|
2143
|
4213
|
|
18
|
14
|
48
|
13
|
Вариант 1
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость первого автомобиля, тогда скорость второго автомобиля на второй половине пути равна  км/ч. Примем расстояние между пунктами за 1. Автомобили были в пути одно и то же время, отсюда имеем: км/ч. Примем расстояние между пунктами за 1. Автомобили были в пути одно и то же время, отсюда имеем: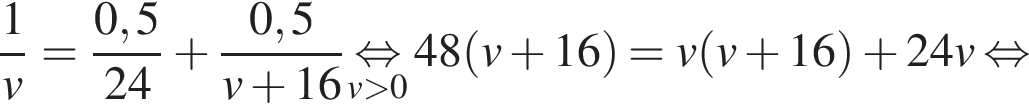 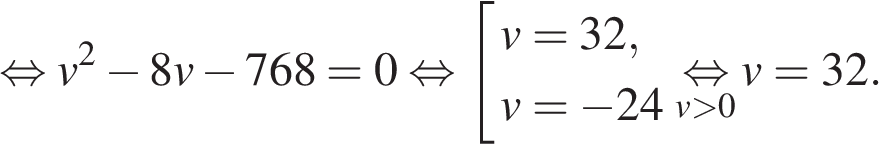 Таким образом, скорость первого автомобиля была равна 32 км/ч. Ответ: 32. Таким образом, скорость первого автомобиля была равна 32 км/ч. Ответ: 32.
В прямоугольном параллелепипеде 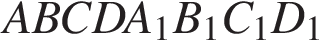 ребро ребро 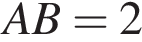 , ребро , ребро  , ребро , ребро 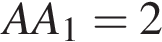 . Точка . Точка 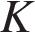 — середина ребра — середина ребра 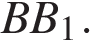 Найдите площадь сечения, проходящего через точки Найдите площадь сечения, проходящего через точки  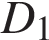 и и 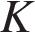 . .
П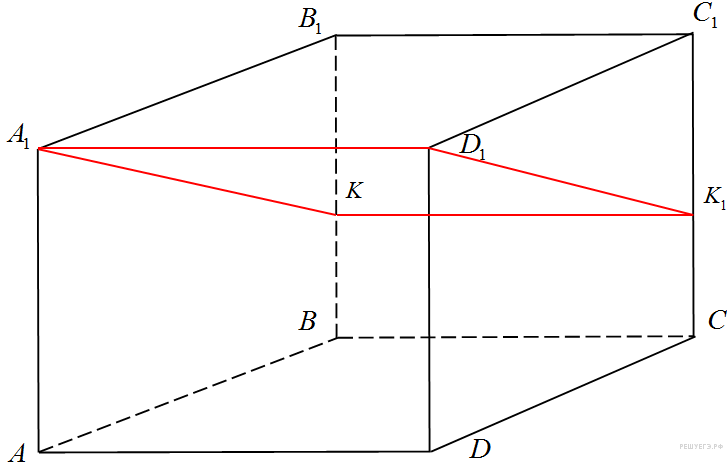 ояснение. ояснение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому четырехугольник  — параллелограмм. Кроме того, ребро — параллелограмм. Кроме того, ребро 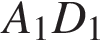 перпендикулярно граням перпендикулярно граням 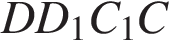 и и 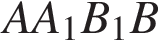 , поэтому углы , поэтому углы 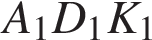 и и 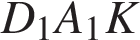 — прямые. Следовательно, сечение — прямые. Следовательно, сечение  — прямоугольник. — прямоугольник.
Из прямоугольного треугольника 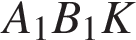 по теореме Пифагора найдем по теореме Пифагора найдем 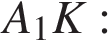
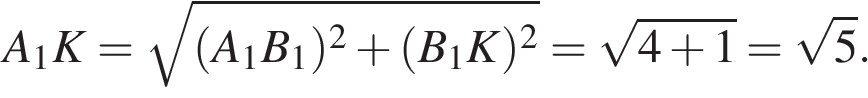
Тогда площадь прямоугольника  равна: равна: Ответ:5. Ответ:5.
а) Решите уравнение 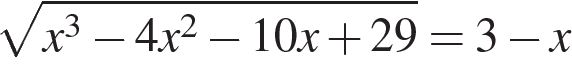 . .
б) Укажите все корни этого уравнения, принадлежащие промежутку 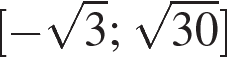 . .
Решение.
а) Решим уравнение:
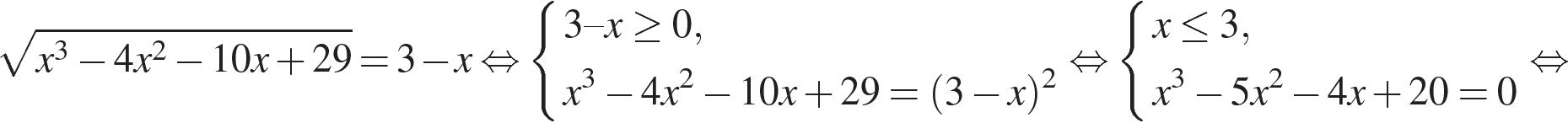
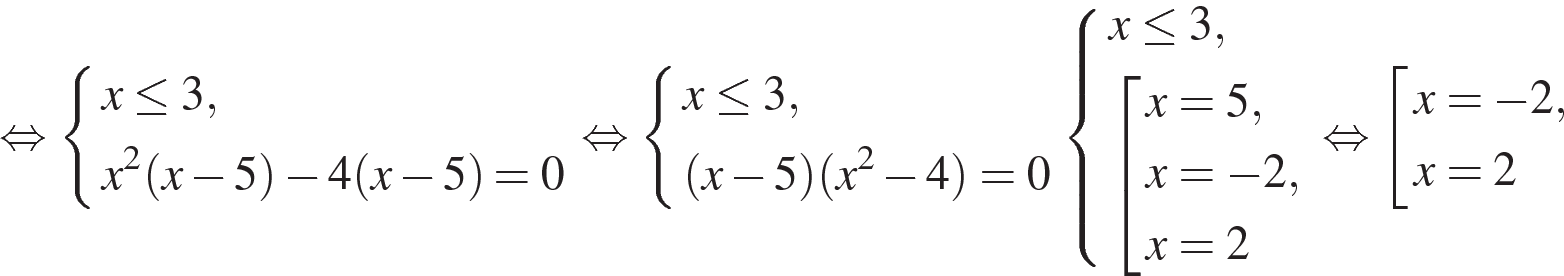
б) Поскольку 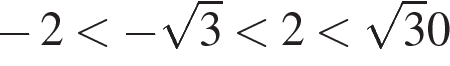 , отрезку , отрезку 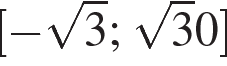 принадлежит только число 2.Ответ: а) принадлежит только число 2.Ответ: а)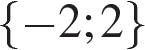 ; б) 2. ; б) 2.
Вариант 2
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение. Пусть км/ч – скорость велосипедиста, тогда скорость автомобилиста равна 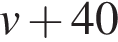 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем: км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем: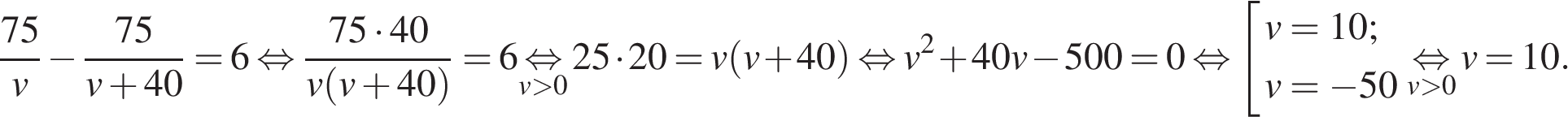
Таким образом, скорость велосипедиста была равна 10 км/ч.Ответ: 10.
В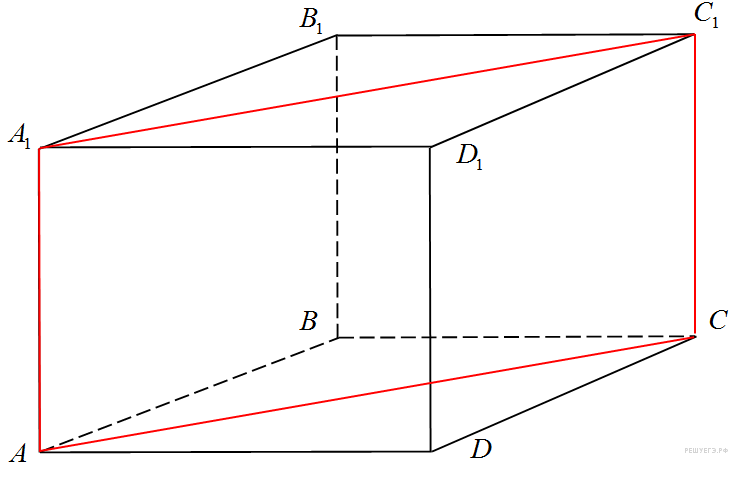 прямоугольном параллелепипеде прямоугольном параллелепипеде 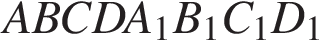 известны длины рёбер: известны длины рёбер:  , , 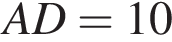 , ,  . Найдите площадь сечения, проходящего через вершины . Найдите площадь сечения, проходящего через вершины 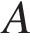 , ,  и и 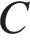 . .
Пояснение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение 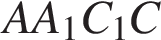 − параллелограмм. Кроме того, ребро − параллелограмм. Кроме того, ребро 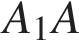 перпендикулярно граням перпендикулярно граням  и и 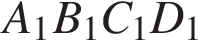 . Поэтому углы . Поэтому углы 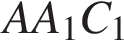 и и 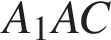 − прямые. Поэтому сечение − прямые. Поэтому сечение 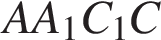 — прямоугольник. — прямоугольник.
Из прямоугольного треугольника 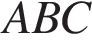 найдем найдем 
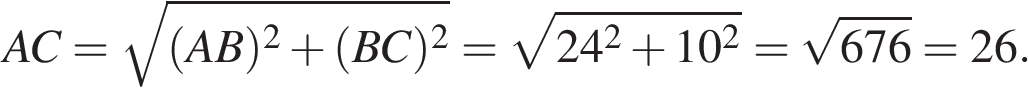
Тогда площадь прямоугольника 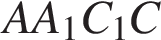 равна: равна: Ответ:572. Ответ:572.
а) Решите уравнение: 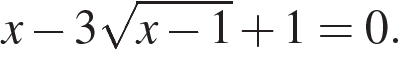
б) Укажите корни этого уравнения, принадлежащие отрезку 
Решение.
а) Запишем исходное уравнение в виде 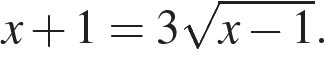 При При 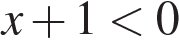 уравнение не имеет корней. При уравнение не имеет корней. При 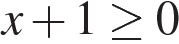 уравнение принимает вид: уравнение принимает вид: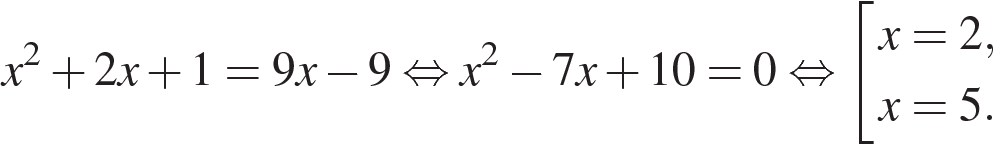
Оба корня удовлетворяют условию 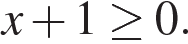 б) Заметим, что б) Заметим, что 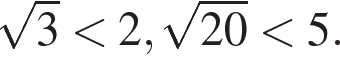 Значит, указанному отрезку принадлежит корень 2.Ответ: а) 2; 5; б) 2. Значит, указанному отрезку принадлежит корень 2.Ответ: а) 2; 5; б) 2.
Вариант 3
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути – со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Решение. Пусть км/ч – скорость первого автомобиля, тогда скорость второго автомобиля на первой половине пути равна 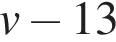 км/ч. Примем расстояние между пунктами за 2. Автомобили были в пути одно и то же время, отсюда имеем: км/ч. Примем расстояние между пунктами за 2. Автомобили были в пути одно и то же время, отсюда имеем:
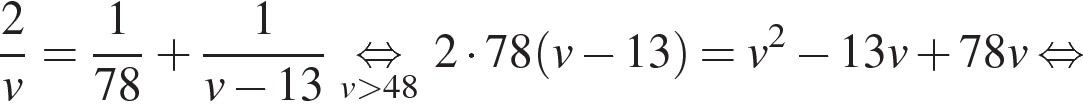 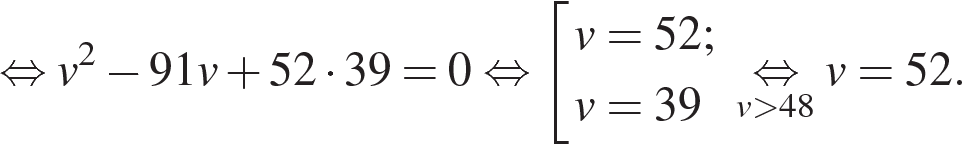
Таким образом, скорость первого автомобиля была равна 52 км/ч.Ответ: 52.
В прямоугольном параллелепипеде известны длины рёбер: AB = 3, AD = = 5, AA1 = 12. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
Пояснение.
С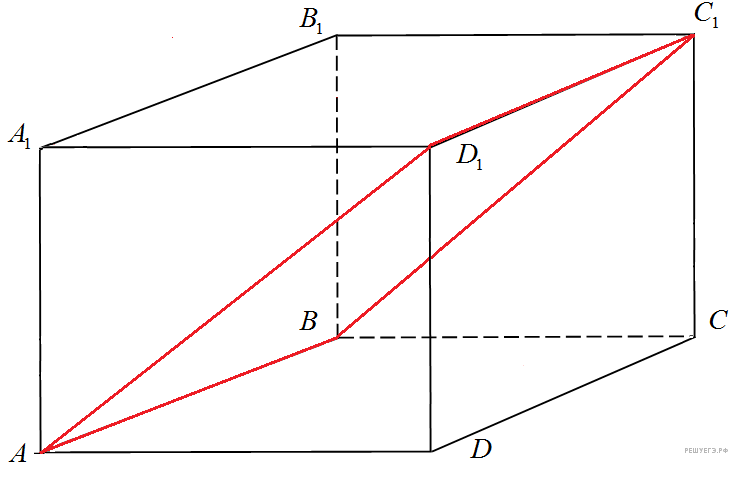 ечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение ечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение  — параллелограмм. Кроме того, ребро — параллелограмм. Кроме того, ребро 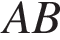 перпендикулярно граням перпендикулярно граням 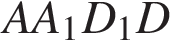 и и 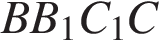 . Поэтому углы . Поэтому углы 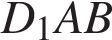 и и 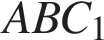 — прямые. Поэтому сечение — прямые. Поэтому сечение  — прямоугольник. — прямоугольник.
Из прямоугольного треугольника 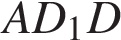 найдем найдем 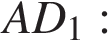
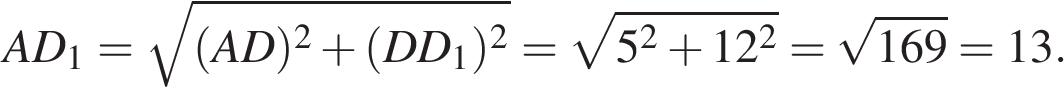
Тогда площадь прямоугольника  равна: равна: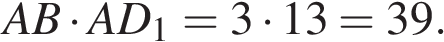 Ответ:39. Ответ:39.
Решите неравенство: 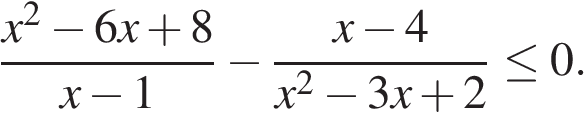
Решение.
Перепишем неравенство в виде:
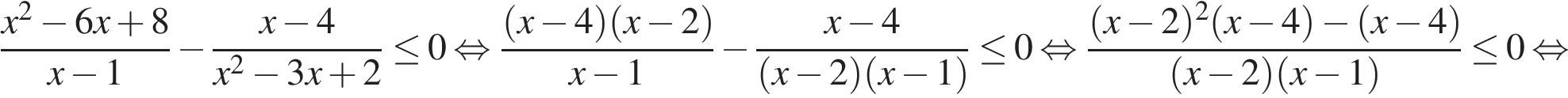
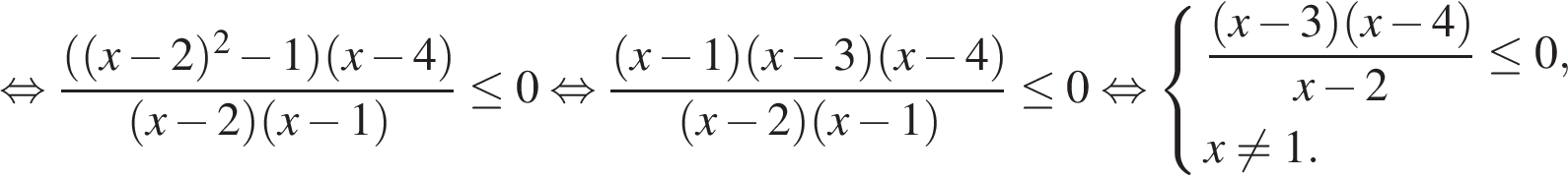 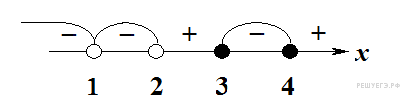 Множество решений исходного неравенства: Множество решений исходного неравенства: 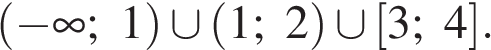 Ответ: Ответ: 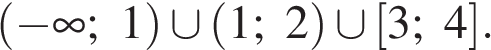
Вариант 4
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
Решение. Пусть км/ч – скорость велосипедиста на пути из B в A, тогда скорость велосипедиста на пути из Aв B равна  км/ч. Сделав на обратном пути остановку на 3 часа, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем: км/ч. Сделав на обратном пути остановку на 3 часа, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем: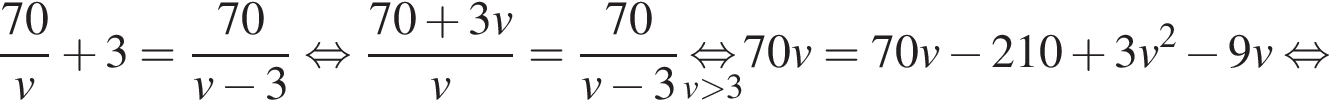 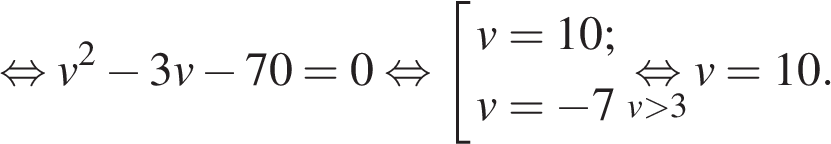
Таким образом, скорость велосипедиста была равна 10 км/ч.Ответ: 10.
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро BC = 4, ребро 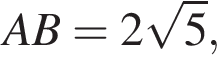 ребро BB1 = 4. Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K. ребро BB1 = 4. Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K.
П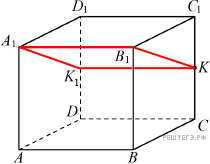 ояснение. ояснение.
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому четырехугольник  — параллелограмм. Кроме того, ребро — параллелограмм. Кроме того, ребро 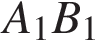 перпендикулярно граням перпендикулярно граням 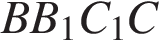 и и 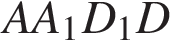 , поэтому углы , поэтому углы 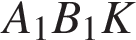 и и 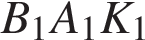 — прямые. Следовательно, сечение — прямые. Следовательно, сечение  — прямоугольник. — прямоугольник.
Из прямоугольного треугольника 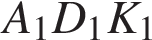 по теореме Пифагора найдем по теореме Пифагора найдем 
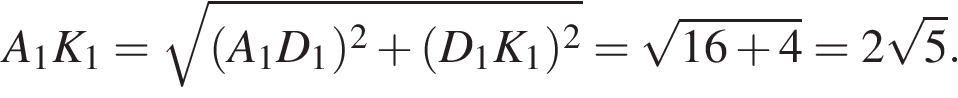 Тогда площадь прямоугольника Тогда площадь прямоугольника 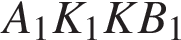 равна: равна: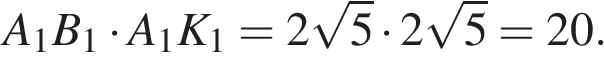 Ответ:20. Ответ:20.
Решите неравенство: 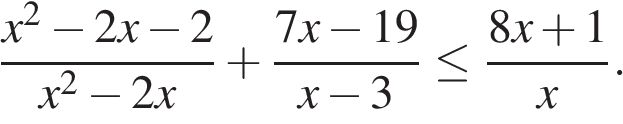
Решение. Решим неравенство методом интервалов:
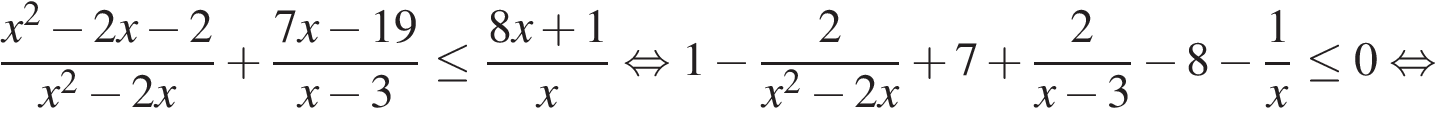
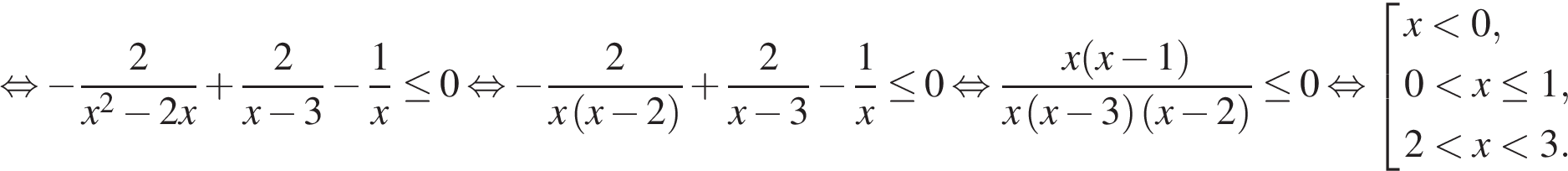
Ответ: 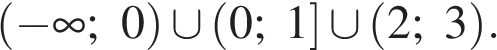 |
|
|
 Скачать 0.83 Mb.
Скачать 0.83 Mb. ояснение.
ояснение.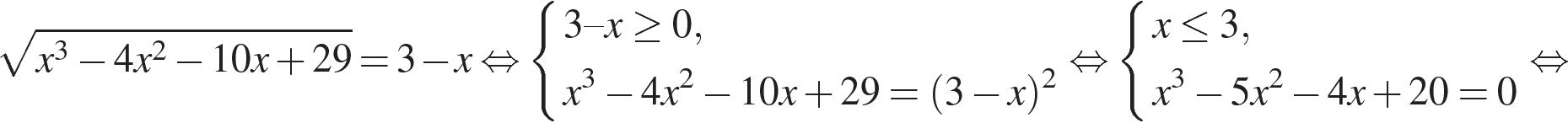
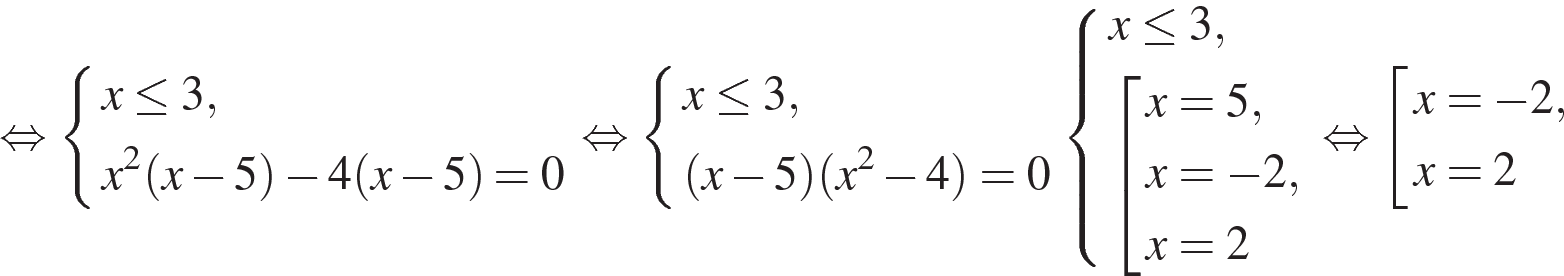
 прямоугольном параллелепипеде
прямоугольном параллелепипеде 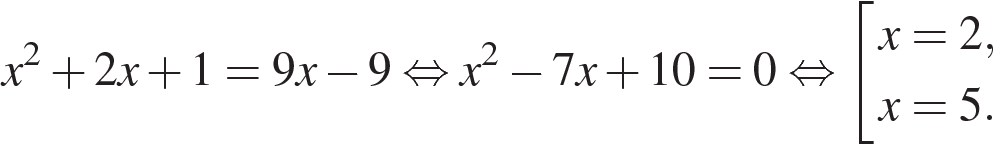
 ечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение
ечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение 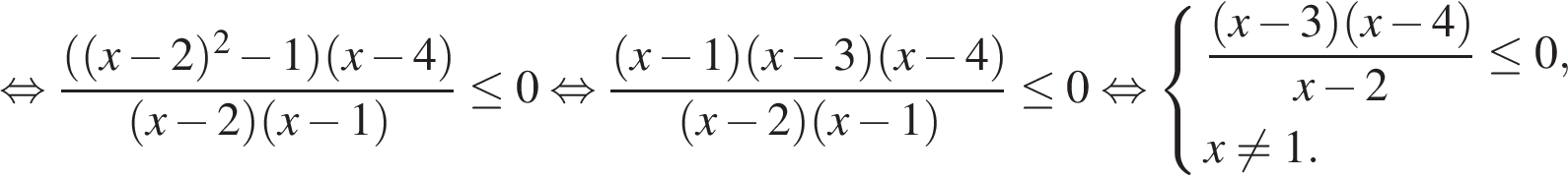
 ояснение.
ояснение.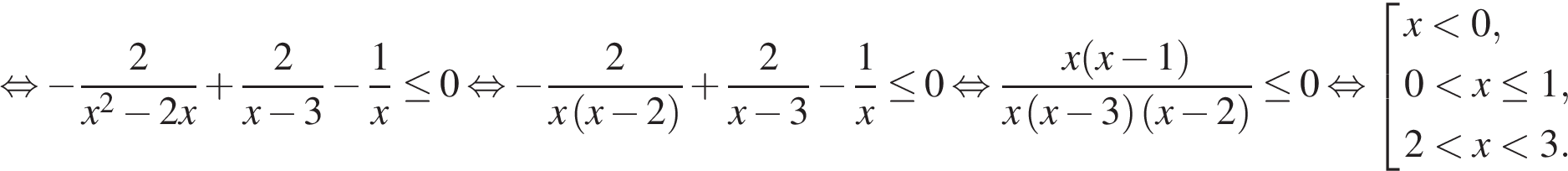

 .Два угла треугольника равны
.Два угла треугольника равны 
 .В треугольнике
.В треугольнике 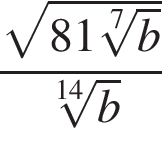 при
при  . Острый угол прямоугольного треугольника равен
. Острый угол прямоугольного треугольника равен 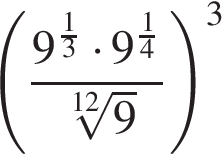 .
. . Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
. Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.