Контрольная работа 2 Метод координат Вариант 1 Найдите координаты и длину вектора, если
 Скачать 17.06 Kb. Скачать 17.06 Kb.
|
|
Контрольная работа № 2 «Метод координат» Вариант 1 1. Найдите координаты и длину вектора 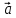 , если , если 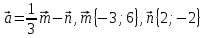 2.Напишите уравнение окружности с центром в точке Т(3;-2), проходящей через точку B(-2;0). 3.Треугольник MNK задан координатами своих вершин: M(-6;1), N(2;4), K(2;-2). а) Докажите, что треугольник MNK – равнобедренный. б) Найдите высоту, проведенную из вершины M. 4.Найдите координаты точки N,лежащей на оси абсцисс и равноудаленной от точек P(2;4) и K(5;-1). 5*. Докажите, что четырехугольник MNKP, заданный координатами своих вершин M(2;2), N(5;3), K(6;6), P(3;-5), является ромбом и вычислите его площадь. Контрольная работа № 2 «Метод координат» Вариант 2 1. Найдите координаты и длину вектора 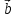 , если , если 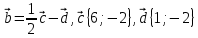 . .2.Напишите уравнение окружности с центром в точке S(2;-1), проходящей через точку B(-3;2). 3.Треугольник FRT задан координатами своих вершин: F(2;-2), R(2;3), T(-2;1). а) Докажите, что треугольник FRT – равнобедренный. б) Найдите высоту, проведенную из вершины F. 4.Найдите координаты точки A,лежащей на оси ординат и равноудаленной от точек B(1;-3) и C(2;0). 5*. В равнобедренном треугольнике основание равно 10 см, а биссектриса, проведенная к основанию, равна 8 см. Найдите медиану, проведенную к боковой стороне. Контрольная работа № 2 «Метод координат» Вариант 3 1. Найдите координаты и длину вектора 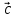 , если , если 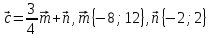 . .2.Напишите уравнение окружности с центром в точке A(-3;2), проходящей через точку B(0;-2). 3.Треугольник FEC задан координатами своих вершин: F(-1;1), E(4;1), C(1;-3). а) Докажите, что треугольник FEC – равнобедренный. б) Найдите медианy, проведенную из вершины Е. 4.Найдите координаты точки N,лежащей на оси абсцисс и равноудаленной от точек P(-1;3) и K(0;2). 5*. В равнобедренном треугольнике основание равно 16 см, а высота, проведенная к основанию, равна 5 см. Найдите медиану, проведенную к боковой стороне. Контрольная работа № 2 «Метод координат» Вариант 4 1. Найдите координаты и длину вектора 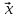 , если , если 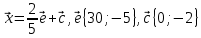 . .2.Напишите уравнение окружности с центром в точке C(2;1), проходящей через точку D(5;5). 3.Треугольник CDE задан координатами своих вершин: C(2;2), D(6;5), E(5;-2). а) Докажите, что треугольник CDE – равнобедренный. б) Найдите биссектрису, проведенную из вершины C. 4.Найдите координаты точки Н, лежащей на оси ординат и равноудаленной от точек N(-2;-1) и K(4;1). 5*. Докажите, что четырехугольник PSQT, заданный координатами своих вершин P(3;0), S(-1;3), Q(-4;-1), T(0;-4), является квадратом и вычислите его площадь. Ответы: Вариант 1 1) 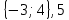 2) 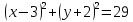 3б) 8 4) (1;0) 5) 8кв.ед. Вариант 2 1) 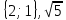 2) 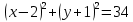 3б) 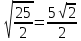 4) (0;-1) Вариант 3 1) 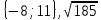 2) 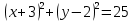 3б) 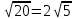 4) (-3;0) 5) 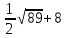 кв.ед. кв.ед.Вариант 4 1) 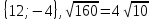 2) 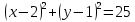 3б) 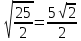 4) (0;3) 5) 25кв.ед. |
