Основы функционального анализа. Основы функционального анализа КР 2 (исправления).doc 2(исправле. Контрольная работа 2 По дисциплине Основы функционального анализа
 Скачать 144.48 Kb. Скачать 144.48 Kb.
|
 Министерство образования Российской Федерации Министерство образования Российской ФедерацииТомский межвузовский центр дистанционного образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра радиоэлектроники и защиты информации Контрольная работа № 2 По дисциплине «Основы функционального анализа» (Учебное пособие «Высшая математика. Интегральное исчисление. Дифференциальные уравнения», Автор Ельцов А.А., 2001г.) Вариант 9 Выполнил студент Специальности 16.08.2014 2.Изменить порядок интегрирования: 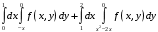 . .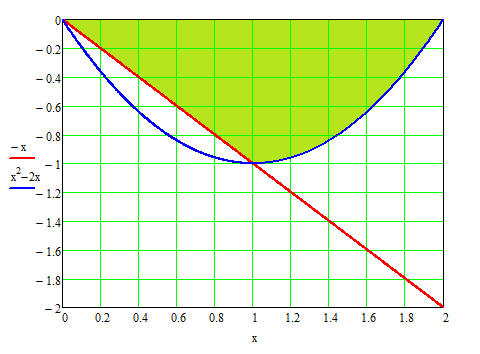 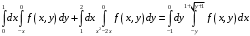 3.Вычислить площадь области, заданной неравенствами 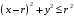 , , 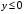 , , 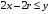 , перейдя предварительно к полярным координатам. , перейдя предварительно к полярным координатам.В полярной системе координат: 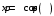 , , 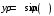 . .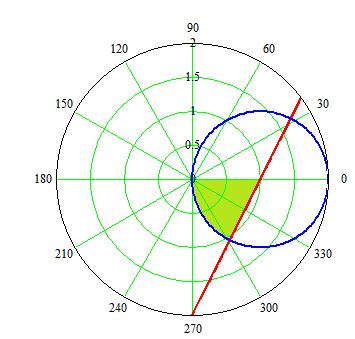 Перенесем начало координат в точку 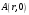 , тогда получим новую систему неравенств: , тогда получим новую систему неравенств: 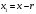 , , 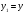 . .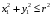 , , 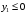 , , 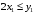 . .Перейдем теперь к полярной системе координат 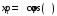 , , 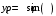 : :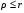 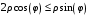 , , 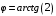 Получим: 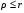 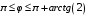 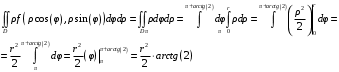 Уравнения области в полярной системе координат: 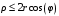 , ,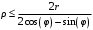 . .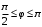 , угол при пересечении двух функций: , угол при пересечении двух функций: 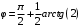 . .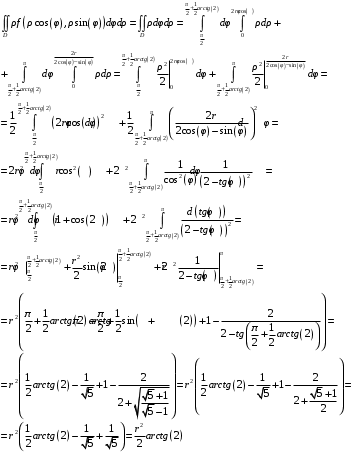 5. Вычислить интеграл (в цилиндрических или сферических координатах) 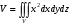 , где V - область, заданная неравенствами: , где V - область, заданная неравенствами: 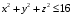 , , 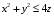 . .Перейдем к цилиндрическим координатам: 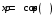 , , 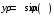 и и 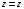 . .Тогда область V будет: 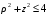 , , 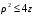 , , 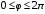 . .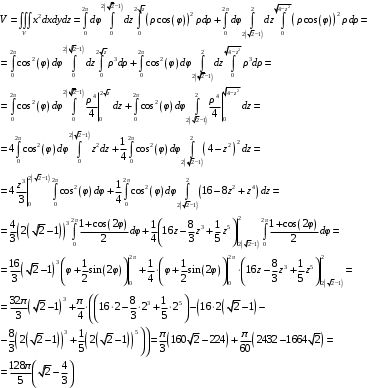 8. Вычислить поток вектора 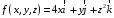 через часть поверхности через часть поверхности  , лежащую в первом октанте. , лежащую в первом октанте.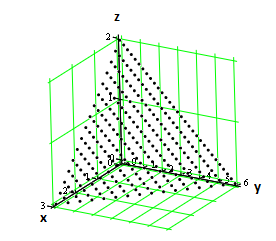 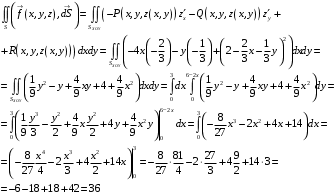 |
