Теория вероятности кр. Теория вероятности кр2 (исправл= E5ния). Контрольная работа 2 По дисциплине Теория вероятности
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
Министерство образования Российской Федерации Томский межвузовский центр дистанционного образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра радиоэлектроники и защиты информации Контрольная работа № 2 По дисциплине «Теория вероятности» (Учебное пособие «Высшая математика 4. Теория вероятностей», автор Магазинников Л.И., 2000г.) Вариант 9 Выполнил студент Специальности 16.08.2014 1.Дана матрица распределения вероятностей системы 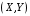  Найти: а) ряды распределения 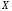 и и 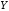 ; б) ; б) 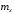 ; в) ; в) 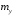 ; г) ; г) 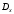 ; д) ; д) 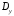 ; е) ; е) 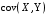 ; ж) ; ж) 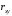 , округлить до 0,01; з) ряд распределения , округлить до 0,01; з) ряд распределения 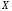 , если , если 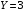 ; и) ; и) 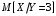 , округлить до 0,01. , округлить до 0,01.а) ряды распределения 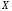 и и 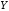 : :Ряды распределения 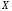 и и 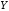 изобразим в виде таблиц. изобразим в виде таблиц.Таблица 1 – Ряд распределения 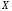  Таблица 2 – Ряд распределения 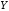  б) математическое ожидание 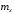 : :Математическое ожидание найдем по формуле: 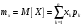 (1) (1)Значения для 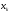 и и 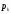 возьмем из ряда распределения для случайной величины возьмем из ряда распределения для случайной величины 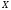 , из таблицы 1: , из таблицы 1: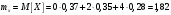 в) математическое ожидание 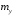 : :Математическое ожидание найдем по формуле, аналогичной формуле (1): 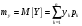 (2) (2)Значения для 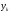 и и 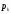 возьмем из ряда распределения для случайной величины возьмем из ряда распределения для случайной величины 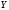 , из таблицы 2: , из таблицы 2: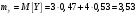 г) дисперсию случайной величины 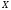 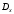 : :Дисперсию найдем по формуле: 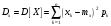 (3) (3)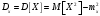 Значения для 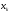 и и 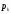 возьмем из ряда распределения для случайной величины возьмем из ряда распределения для случайной величины 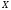 , из таблицы 1, а математическое ожидание , из таблицы 1, а математическое ожидание 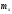 найдено ранее: найдено ранее: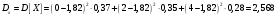 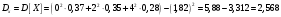 д) дисперсию случайной величины 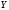 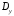 : :Дисперсию найдем по формуле: 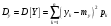 (4) (4)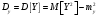 Значения для 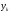 и и 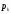 возьмем из ряда распределения для случайной величины возьмем из ряда распределения для случайной величины 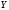 , из таблицы 2, а математическое ожидание , из таблицы 2, а математическое ожидание 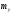 найдено ранее: найдено ранее: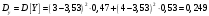 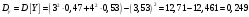 е) ковариацию случайных величин 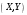 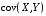 : :Ковариацию найдем по формуле: 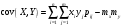 (5) (5)Значения для 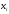 , , 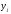 и соответствующую им вероятность и соответствующую им вероятность 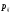 возьмем из матрицы распределения вероятностей системы возьмем из матрицы распределения вероятностей системы 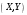 заданной в задании, а математические ожидания заданной в задании, а математические ожидания 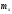 и и 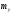 найдены ранее: найдены ранее: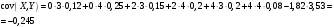 ж) коэффициент корреляции 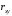 : :Коэффициент корреляции найдем по формуле: 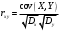 (6) (6)Значения для формулы 6 были найдены ранее, подставим их и получим: 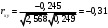 з) ряд распределения 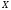 , если , если 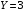 : :Ряд распределения 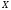 , если , если 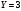 , найдем по формуле: , найдем по формуле: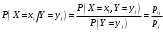 (7) (7)Значения 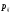 возьмем из матрицы распределения вероятностей системы возьмем из матрицы распределения вероятностей системы 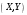 а а 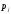 из таблицы 2 ряда распределения из таблицы 2 ряда распределения 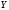 , подставим их и получим, таблицу 3. , подставим их и получим, таблицу 3.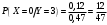 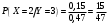 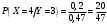 Таблица 3 – Ряд распределения 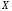 , если , если 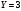  и) условное математическое ожидание 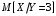 : :Условное математическое ожидание найдем, используя формулу (1) и таблицу 3: 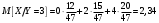 2.Дана плотность распределения вероятностей системы 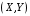 : :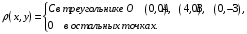 Найти: а) константу С: б) 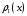 , , 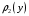 ; в) ; в) 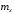 ; г) ; г) 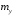 ; д) ; д) 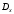 ; е) ; е) 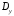 ; ж) ; ж) 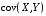 ; з) ; з) 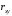 ; и) ; и) 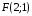 ; к) ; к) 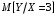 . .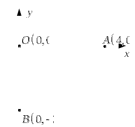 Рисунок 1 – Область 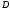 . .а) найти константу 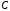 : :Константа 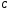 находится из условия нормировки: находится из условия нормировки: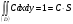 , (8) , (8)Воспользуемся формулой (8) для нахождения коэффициента 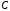 : :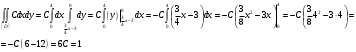 Таким образом, получим: 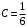 . .Тогда плотность распределения системы 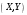 , равна: , равна: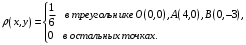 б) плотность распределения случайной величины 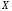 , , 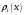 и случайной величины и случайной величины 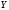 , , 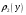 : :Плотность распределения случайной величины 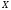 , найдем по формуле: , найдем по формуле: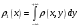 (9) (9)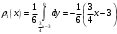 , тогда , тогда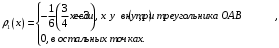 Плотность распределения случайной величины 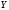 , найдем по формуле: , найдем по формуле: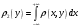 (10) (10)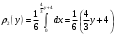 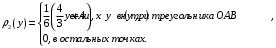 в) математическое ожидание 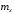 : :Математическое ожидание найдем по формуле: 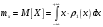 (11) (11)Значение 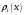 найдено ранее, тогда: найдено ранее, тогда: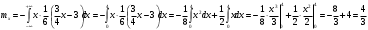 г) математическое ожидание 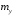 : :Математическое ожидание найдем по формуле: 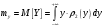 (12) (12)Значение 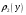 найдено ранее, тогда: найдено ранее, тогда: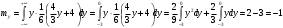 д) дисперсию 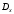 : :Дисперсию найдем по формуле: 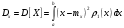 (13) (13)Значение 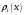 найдено ранее, тогда: найдено ранее, тогда: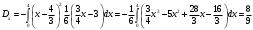 е) дисперсию 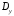 : :Дисперсию найдем по формуле: 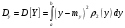 (14) (14)Значение 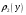 найдено ранее, тогда: найдено ранее, тогда: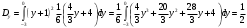 ж) ковариацию случайных величин 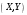 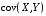 : :Ковариацию найдем по формуле: 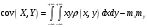 (15) (15)Значения математических ожиданий  и и  найдены ранее: найдены ранее: з) коэффициент корреляции  : :Коэффициент корреляции найдем по формуле (6): 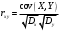 Значения для формулы 6 были найдены ранее, подставим их и получим: 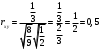 и) функцию распределения системы 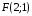 : :Функцию распределения системы, найдем по формуле: 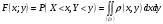 (16) (16)На рисунке 2 изображена область D и точка M с координатами  , функцию распределения необходимо найти. , функцию распределения необходимо найти.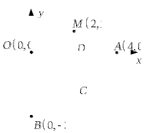 Рисунок 2 – Область D и точка М. В формуле (16) область D в данном случае является трапецией OBCD. Тогда искомое значение функции распределения системы, получим: 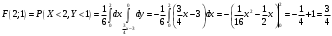 к) условное математическое ожидание 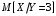 : :Условное математическое ожидание найдем, используя формулу: 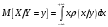 (17) (17)Для формулы (17) найдем условную плотность распределения, по формуле: 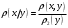 (18) (18)Подставим значения в формулу (18): 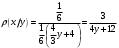 Подставим полученное значение в формулу (17) и найдем условное математическое ожидание: 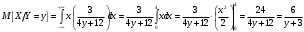 В полученное выражение подставим 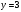 и получим искомое значение: и получим искомое значение: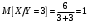 |
