Гуков Физика 2. Контрольная работа 2 по физике Гуков С. В. Группа нд (аб) зд81 Шифр 1 8 0 0 1 4 8 1 9 Проверил

• Название: Контрольная работа 2 по физике Гуков С. В. Группа нд (аб) зд81 Шифр 1 8 0 0 1 4 8 1 9 Проверил
• Дата: 28.04.2019
• Размер: 372.5 Kb.
• Имя файла: Гуков Физика 2.doc
• Тип: Контрольная работа; #75488

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

Тихоокеанский государственный университет


Контрольная работа №2

по физике

Выполнил: Гуков С.В.

Группа: НД (аб) зд-81

Шифр: 1 8 0 0 1 4 8 1 9

Проверил:

Поскольку для рисунка 32 с ромбом угол в методичке не задан,

то решаем по рисунку 33 – с квадратом.

Задача 1.

В вершинах квадрата расположены бесконечно длинные проводники. Токи I₁ = I₂ = 3 А направлены «от нас», а ток I₃ = I₄ = 3 А направлен «на нас». Сторона квадрата a = 6 см. Найти вектор магнитной индукции в точке A, расположенной в центре геометрической фигуры.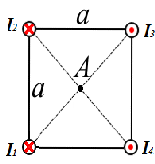

Дано:
А
А
А
А
см	м

Решение.

По принципу суперпозиции результирующий вектор магнитной индукции в точке A, расположенной в центре геометрической фигуры, равен:

.

Определим направление векторов магнитной индукции 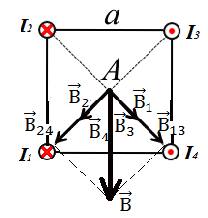(по правилу буравчика), созданных в центре фигуры каждым током в отдельности, и изобразим на рисунке. Также построим результирующий вектор .

Каждый проводник от точки A отстоит на расстояние:

.

Так как токи в проводниках и расстояния до точки A одинаковые, то модули векторов магнитной индукции также будут одинаковыми и равными:

,

где Гн/м – магнитная постоянная.

Направления векторов и совпадают, поэтому для них векторную сумму можно заменить алгебраической:

;

;

Тл.

Для векторов и получаем аналогично:

;

;

Тл.

Векторы и перпендикулярны, поэтому модуль результирующего вектора магнитной индукции равен:

;

Тл.

Ответ: Тл.

Задача 2.

Заряженная частица q = 1,6·10^-19 Кл и массой m = 9,1·10^-31 кг прошла ускоряющую разность потенциалов U = 10³ В и влетела ортогонально силовым линиям в однородное магнитное поле, с вектором магнитной индукции B = 0,001 Тл. Найти радиус R вращения заряженной частицы.

Дано:
Кл
кг
В
Тл

Решение.

На движущуюся в магнитном поле со скоростью заряженную частицу действует сила Лоренца:

;

.

Так как частица влетела ортогонально силовым линиям (), то :

. (2.1)

Направление силы Лоренца 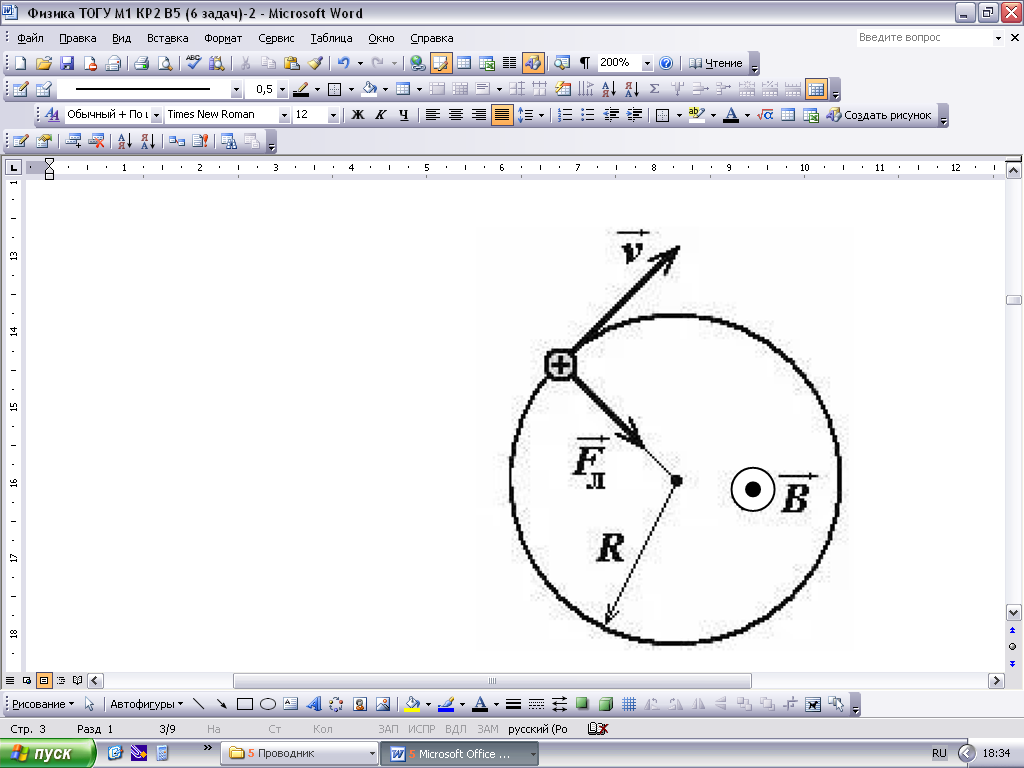определяется по правилу «левой руки».


При этом сила Лоренца сообщает частице только нормальное ускорение:

. (2.2)

Частица будет двигаться равномерно по окружности радиуса .

Запишем II-й закон Ньютона для частицы:

.

Или, с учётом (2.1) и (2.2):

.

Отсюда выразим радиус окружности:

. (2.3)

Из условия равенства работы, совершённой ускоряющим электрическим полем над частицей, и приобретённой ею кинетической энергии:

,

найдём скорость заряженной частицы:

;

;

м/с.

Теперь по формуле (2.3) найдём радиус вращения частицы:

м = 11 см.

По условию задачи, частица имеет положительный элементарный заряд и массу, равную массе электрона. Следовательно, это позитрон. Заметим, что отрицательно заряженный электрон будет вращаться по окружности такого же радиуса, но в обратную сторону.

Ответ: см.

Задача 3.

На тонкую плёнку жидкости, имеющую показатель преломления n₁, падает перпендикулярно к поверхности свет с длиной волны  = 500 нм. Наименьшая толщина d плёнки, при которой отражённый свет будет ослаблен в результате интерференции, равна 0,179 мкм. Найти показатель преломления плёнки.

Дано:
нм
мкм	нм

Решение.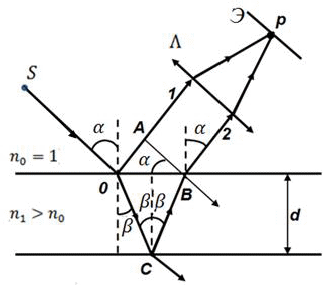


На рисунке представлена тонкая плёнка толщиной d. На неё под углом  к нормали падает параллельный пучок лучей. Луч SO, попадая в точку O, частично отражается (луч 1), частично преломляется (OC).

Преломленный луч OC испытывает отражение от нижней поверхности плёнки в точке C и, преломляясь в точке B, выходит из плёнки (луч 2). Лучи 1 и 2 параллельны и когерентны, так как образованы от одного луча SO.

Если на пути этих лучей поставить линзу (), то они пересекутся на экране (Э) в точке P.

Будем считать, что плёнка находится в воздухе (показатель преломления n₀ = 1). Найдём оптическую длину пути лучей 1 и 2. Для этого из точки B проведём нормаль BA к лучу 1. Оптические пути лучей 1 и 2 от точек A и B до места их наложения одинаковы. Найдём оптические пути лучей 1 и 2 от точки O до точек A и B.

Оптическая длина пути луча 1:

.

Оптическая длина пути луча 2:

.

Тогда оптическая разность хода лучей 2 и 1:

. (3.1)

Из рисунка следует:

; (3.2)

; (3.3)

. (3.4)

По закону преломления света:

. (3.5)

Из (3.1)-(3.5) получаем:



Учитывая, что для воздуха и что при отражении луча 2 от границы раздела оптически менее плотной среды с оптически более плотной (точка O) происходит потеря полуволны, окончательно для оптической разности хода лучей 2 и 1 получим:

. (3.6)

По условию задачи, отражённый свет должен быть ослаблен, то есть оптическая разность хода лучей 2 и 1 должна быть равна нечётному числу полуволн:

, где . (3.7)

Приравнивая правые части (3.6) и (3.7), получим условие интерференционного минимума в отражённом свете для тонкой плёнки, находящейся в воздухе:

;

;

. (3.8)

Поскольку свет падает перпендикулярно (), а толщина плёнки должна быть минимальной (), из (3.8) получим:

;

. (3.9)

Из (3.9) выразим показатель преломления плёнки:

;

.

Ответ: .

Задача 4.

При облучении металла с работой выхода A_вых светом, имеющим частоту v и длину волны , наблюдается фотоэффект. Красная граница фотоэффекта _кр = 280 нм, кинетическая энергия фотоэлектронов T = 16 эВ, максимальная скорость вырванных фотоэлектронов . Найти , , A_вых.

Дано:
нм	м
эВ	Дж

Решение.

Уравнение Эйнштейна для внешнего фотоэффекта имеет вид:

.

Зная красную границу фотоэффекта, можем найти работу выхода электронов из металла:

,

где Дж∙с – постоянная Планка;

м/с – скорость распространения света в вакууме;

Дж эВ.

Кинетическая энергия выбитых фотоэлектронов:

.

Отсюда найдём скорость фотоэлектронов, вырванных из металла:

;

;

м/с = 2,4 Мм/с.

Связь между частотой и длиной волны фотона:

.

Из уравнения Эйнштейна найдём длину волны света, которым облучают металл:

;

м = 61 нм.

Ответ: нм, Мм/с, эВ.

Задача 5.

Дан радиоактивный изотоп с периодом полураспада T. Постоянная распада  = ln2/T. Если в нём в момент времени t₀ = 0 имеется N₀ радиоактивных ядер, то через промежуток времени t = 8 сут из них останется нераспавшимися N ядер. Отношение N/N₀ выражает долю оставшихся ядер, а (1 – N/N₀) = 75 % выражает долю распавшихся ядер. Определить период полураспада T.

Дано:
сут

Решение.

Так как доля распавшихся ядер велика, то применим закон распада в интегральной форме:

.

Доля распавшихся за время ядер:

;

.

Отсюда выразим постоянную полураспада:

;

;

.

Найдём период полураспада , учитывая его связь с постоянной распада :

;

сут.

Ответ: сут.

Задача 6.

При соударении дейтрона с ядром атома бериллия ⁹₄Be произошла ядерная реакция

⁹₄Be + ²₁H = ¹₀n + ^A_ZX,

в результате которой образовалось дочернее ядро ^A_ZX и нейтрон. Записать уравнение ядерной реакции и определить дефект массы и энергию связи этого ядра.

Дано:

Решение.

Для определения массового числа дочернего ядра используем закон сохранения массовых чисел:

.

Для определения зарядового числа дочернего ядра используем закон сохранения зарядовых чисел:

.

По таблице Менделеева определяем, что дочерним ядром является ядро изотопа бора .

Запишем полностью ядерную реакцию:

.

Дефект массы ядра Δm есть разность между суммой масс свободных нуклонов (протонов и нейтронов), из которых состоит ядро, и массой ядра:

, (6.1)

где – число протонов;

– число нейтронов.

Массу ядра можно получить, если из массы атома вычесть массу электронов, образующих электронную оболочку атома, число которых равно зарядовому числу ядра:

. (6.2)

Подставляя (6.2) в (6.1), получим:

;

;

, (6.3)

где – масса атома водорода .

Подставляя в (6.3) числовые значения атомных масс (в а. е. м.), получим:

а. е. м.

В соответствии с законом пропорциональности массы и энергии, энергия связи ядра равна:

, (6.4)

где МэВ/а. е. м. – квадрат скорости света (выражен во внесистемных единицах);

Подставляя в (6.4) результат расчёта по формуле (6.3), получим:

МэВ.

Ответ: а. е. м., МэВ, .