Практическая работа 3 (шаблон). Контрольная работа 3 Обработка экспериментальных данных при технических прямых экспериментах и косвенных данных
 Скачать 100.78 Kb. Скачать 100.78 Kb.
|
|
Контрольная работа №3 Обработка экспериментальных данных при технических прямых экспериментах и косвенных данных Цель работы: обработка экспериментальных данных при технических измерениях. Задача Прибор для измерения температуры окружающего воздуха аттестуется по стандартной температуре – 20 оС. При n измерениях получены результаты, оС: Бобров, Власова, Дюков, Заведеев
Пендюр, Пешков, Рябчинский
Саматов, Слюнкин, Терентьев
Ухова, Чинов, Чумак, Шлычкова
Оценить систематическую погрешность измерений и ширину доверительного интервала при доверительной вероятности 0,95. Решение Определяем среднее значение полученных результатов измерений по зависимости: 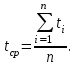 (3.1) (3.1)Разница между истинным значением измеряемой величины и средним значением результатов измерений и будет систематической погрешностью: 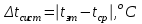 (3.2) (3.2)Ширину доверительного интервала – 2Δλ определяем как в предыдущей работе: 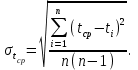 (3.3) (3.3)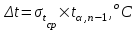 Таким образом, ширина доверительного интервала составляет 2Δt= …. oC. Анализ промахов Теоретическая часть: Отдельным типом погрешностей являются промахи (или грубые ошибки). Под промахами имеются в виду результаты с аномальными числовыми значениями. Причиной промаха может быть, например, сбой аппаратуры. Если экспериментатор записывает показания прибора в протокол измерений, то он может поставить ложную цифру из-за усталости или невнимательности. Промах должен быть исключен из полученной серии результатов измерений. Однако отбрасывать некоторый результат измерения как промах, руководствуясь только субъективным мнением, некорректно. Случайные погрешности могут в принципе принимать весьма большие значения. Следовательно, необходима определенная математическая процедура, позволяющая отличить промах от результата с допустимой (хотя и большой по величине) случайной погрешностью. При анализе промахов обычно принимают, что случайные погрешности имеют гауссово (нормальное) распределение вероятностей. При этом к результатам измерений применимо правило трех сигм. Правило трех сигм (3 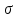 ) – не менее чем с 99,7 % достоверностью значения нормально распределенной случайной величины лежат в интервале [ ) – не менее чем с 99,7 % достоверностью значения нормально распределенной случайной величины лежат в интервале [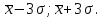 ]. ]. Задача При измерении фактической температуры воздуха на входе в двигатель были получены следующие значения, оС: Для всех вариантов
Проверить, является ли пятое измерение промахом? Решение Доказательство справедливости процедуры поиска промахов приводится в курсах теории вероятностей и математической статистики. Процедуру анализа аномальных результатов, основанную на этом правиле, проводят в несколько этапов: 1. Выберем доверительную вероятность α = 0,95. Из совокупности измерений t1, …, tnвременно исключаем «подозрительный» результат, который заметно отличается от всех остальных, например t5 = 25,9 оС. 2. Вычисляем с реднее статистическое значение оставшихся семи значений результатов измерений ti (i ≠ 5), используя формулу: 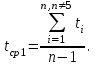 (3.4) (3.4)3. Для α=0,95 и числа степеней свободы 8–2= 6 извлечем из таблицы значение коэффициента Стьюдента t0,95,6 = 2,447. Рассчитываем ширину интервала по формуле: 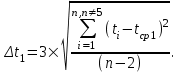 (3.5) (3.5)Обращаем внимание, что в сумме под корнем отсутствует слагаемое с «подозрительным» результатом измерения t5. 4. Проверяем условие: 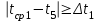 . (3.6) . (3.6)В случае выполнения условия «подозрительное» значение t5считается промахом и исключается из совокупности результатов измерений. При невыполнении условия (3.6) отклонение результата t5от остальных значений ti серии считается допустимым, и значение t5не исключается из набора результатов. Таблица 3.1. Таблица t-распределения t – случайная величина, распределённая по закону Стьюдента с числом степеней свободы n 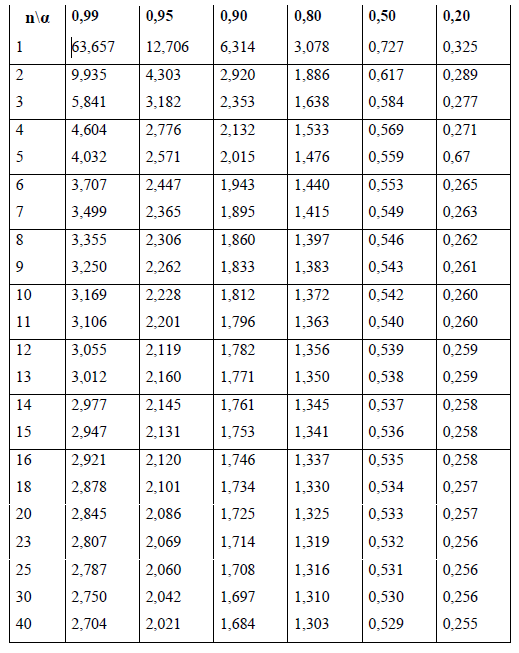 |
