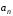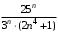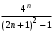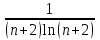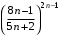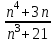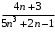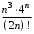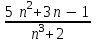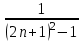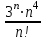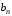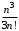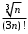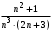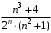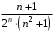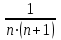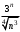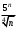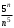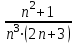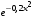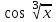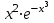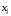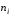Контрольная математика. задание. Контрольная работа 5 по курсу Теории вероятностей и математической статистики (раздел 10 задачи 1, 2, 3, 4, 5). Контрольная работа 4
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
2 курс: контрольная работа № 4 (раздел 4.6: задачи 4.1, 4.2, 4.3, 4.4; раздел 5.7: задачи 5.2, 5.3); контрольная работа № 5 по курсу «Теории вероятностей и математической статистики» (раздел 7.10: задачи 7.1, 7.2, 7.3, 7.4, 7.5). КОНТРОЛЬНАЯ РАБОТА №4 4.6. Контрольные задания по теме «Ряды» Задача 4.1. Исследовать сходимость числового ряда 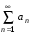 (табл. 4.1). (табл. 4.1).Таблица 4.1
Задача 4.2. Найти область сходимости степенного ряда 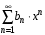 (табл. 4.2). (табл. 4.2).Таблица 4.2
Задача 4.3. Вычислить определенный интеграл 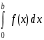 с точностью до 0,0001. Для этого подынтегральную функцию разложить в степенной ряд (табл. 4.3). с точностью до 0,0001. Для этого подынтегральную функцию разложить в степенной ряд (табл. 4.3). Таблица 4.3
Задача 4.4. Разложить функцию f(x) в ряд Фурье в интервале (a, b) (табл. 4.4). Таблица 4.4
5.7. Контрольные задания по теме «Дифференциальные уравнения» Задача 5.2. Найти общее решение дифференциального уравнения первого порядка (по вариантам): 1. 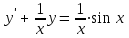 . 2. . 2. 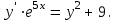 3. 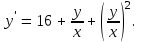 4. 4. 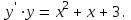 5. 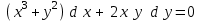 . 6. . 6. 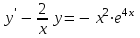 . . 7. 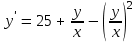 . 8. . 8. 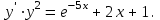 9. 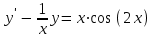 . 0. . 0. 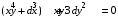 . .Задача 5.3. Найти общее решение дифференциального уравнения второго порядка (по вариантам): 1. 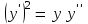 . 2. . 2. 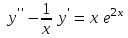 . . 3. 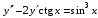 . 4. . 4. 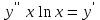 . . 5. 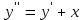 . 6. . 6. 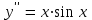 . . 7. 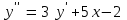 . 8. . 8. 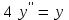 . . 9. 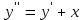 . 0. . 0. 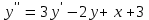 . . Контрольная работа №5 7.10. Контрольные задания по теме «Основы теории вероятностей и математической статистики» Номер варианта равен последней цифре зачетной книжки студента. Задача 7.1. Две лампочки соединены в электрической цепи параллельно. Вероятность того, что первая лампочка выйдет из строя равна 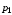 , а вероятность неисправности второй лампочки равна , а вероятность неисправности второй лампочки равна 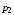 . Найти вероятность того, что: . Найти вероятность того, что: а) света не будет; б) свет будет.
Задача 7.2. В урне находится k белых, M красных и rчерных шаров. Наудачу вынимаются n шаров. Найти вероятность того, что из них окажется: а) 2 белых; б) все красные.
Задача 7.3. В ящике находится k деталей, принадлежащих цеху № 1, M деталей – цеху № 2 и r деталей – цеху № 3. Вероятность того, что деталь окажется бракованной для цеха № 1, равна 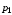 , для цеха № 2 – , для цеха № 2 – 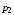 , , а цех № 3 производит n% брака. Наудачу ОТК отбирает на проверку деталь, найти вероятность того, она окажется стандартной.
Задача 7.4. Выполнены многократные измерения длины объекта. Требуется построить доверительный интервал с надежностью 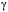 для оценки математического ожидания количественного признака X – неизвестной длины объекта. Данные измерений приведены в таблице по вариантам. для оценки математического ожидания количественного признака X – неизвестной длины объекта. Данные измерений приведены в таблице по вариантам.Вариант 1. 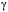 = 0,95 = 0,95
Вариант 2. 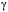 = 0,9 = 0,9
Вариант 3. 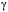 = 0,95 = 0,95
Вариант 4. 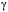 = 0,9 = 0,9
Вариант 5. 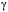 = 0,95 = 0,95
Вариант 6. 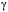 = 0,9 = 0,9
Вариант 7. 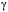 = 0,9 = 0,9
Вариант 8. 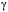 = 0,95 = 0,95
Вариант 9. 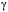 = 0,9 = 0,9
Вариант 0.  = 0,95 = 0,95
Задача 7.5. Для выборки объема n, определить среднее выборочное, выборочную дисперсию, «исправленную» выборочную дисперсию. Построить таблицу, содержащую интервальный вариационный ряд. Построить гистограмму, график эмпирической функции распределения, если выборка задана по вариантам. Вариант 1. Выборка: 18; 19; 21; 30; 36; 34; 19; 21; 30; 35; 19; 18; 21; 21; 22; 18; 30; 23; 19; 28; 21; 30. Вариант 2. Выборка: 19; 19; 21; 30; 33; 34; 19; 21; 30; 35; 35; 19; 18; 21; 36; 21; 22; 18; 22; 19; 28; 21. Вариант 3. Выборка: 18; 18; 21; 34; 34; 19; 21; 30; 35; 19; 18; 21; 36; 21; 22; 18; 30; 23; 19; 28; 21; 30. Вариант 4. Выборка: 17; 19; 21; 30; 36; 34; 17; 21; 30; 19; 18; 21; 21; 39; 22; 18; 30; 23; 19; 40; 28; 21. Вариант 5. Выборка: 28; 19; 21; 30; 34; 19; 28; 30; 35; 36; 19; 18; 21; 21; 22; 18; 30; 23; 19; 21; 30; 18. Вариант 6. Выборка: 38; 39; 30; 36; 34; 39; 30; 35; 36; 36; 40; 49; 45; 40; 36; 22; 30; 23; 40; 28; 21; 30. Вариант 7. Выборка: 38; 29; 21; 40; 36; 34; 21; 30; 35; 36; 21; 36; 40; 40; 21; 36; 22; 30; 23; 40; 28; 21. Вариант 8. Выборка: 28; 21; 30; 36; 24; 21; 30; 35; 36; 19; 18; 21; 26; 21; 36; 22; 18; 30; 23; 28; 21; 20. Вариант 9. Выборка: 29; 21; 30; 26; 34; 30; 35; 36; 31; 36; 40; 39; 40; 21; 36; 24; 30; 23; 40; 28; 21; 40. Вариант 0. Выборка: 38; 31; 30; 36; 34; 31; 30; 35; 36; 21; 36; 40; 40; 21; 36; 32; 30; 25; 19; 40; 28; 21. 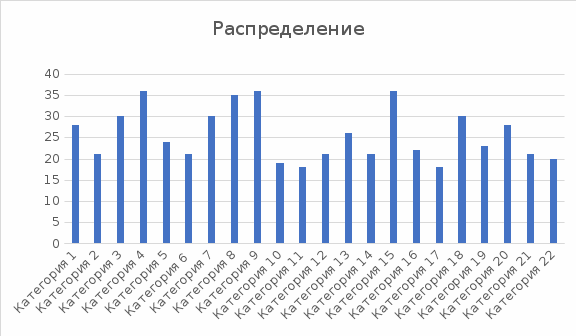  |