Контрольная работа 6 по теме Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений

• Название: Контрольная работа 6 по теме Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений
• Дата: 02.08.2022
• Размер: 14.21 Kb.
• Имя файла: phpFL4Yv2_Kontr-rabota-6-algebra-8-klass.docx
• Тип: Контрольная работа; #639588

Контрольная работа № 6 по теме «Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений»

Вариант 1

1. Разложите на множители квадратный трёхчлен:

1) x² − 5x − 24; 2) 3x² − 10x − 8.

2. Решите уравнение:

1) x⁴ − 3x² − 4 = 0; 2) .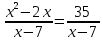

3. Сократите дробь .

4. Решите уравнение

5. Лодка прошла 16 км по течению реки и 18 км против течения, затратив на путь против течения на 1 ч больше, чем на путь по течению. Найдите собственную скорость лодки, если скорость течения реки составляет 1 км/ч.

Контрольная работа № 6 по теме «Квадратный трёхчлен. Решение уравнений, сводящихся к квадратным уравнениям. Решение задач с помощью рациональных уравнений»

Вариант 2

1. Разложите на множители квадратный трёхчлен:

1) x² + 3x − 40; 2) 6x² + x − 12.

2. Решите уравнение:

1) x⁴ − 15x² − 16 = 0; 2) .

3. Сократите дробь .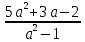

4. Решите уравнение .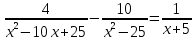

5. Моторная лодка прошла 48 км по течению реки и 70 км против течения, затратив на путь по течению на 1 ч меньше, чем на путь против течения. Найдите собственную скорость лодки, если скорость течения реки составляет 2 км/ч.

Классная работа

1. Разложите на множители квадратный трёхчлен:

1) x² − 2x − 24; 2) 3x² + 14x − 5.

2. Решите уравнение:

1) x⁴ + 2x² − 8 = 0; 2) .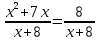

3. Сократите дробь .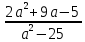

4. Решите уравнение .

5. Теплоход прошёл 72 км против течения реки и 56 км по течению, затратив на путь против течения на 1 ч больше, чем на путь по течению. Найдите собственную скорость теплохода, если скорость течения реки составляет 2 км/ч.
Домашняя работа

1. Разложите на множители квадратный трёхчлен:

1) x² + x − 30; 2) 2x² − 7x − 9.

2. Решите уравнение:

1) x⁴ + 6x² − 27 = 0; 2) .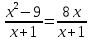

3. Сократите дробь .

4. Решите уравнение .

5. Катер прошёл 64 км против течения реки и 38 км по течению, затратив на путь по течению на 1 ч меньше, чем на путь против течения. Найдите собственную скорость катера, если скорость течения реки составляет 3 км/ч.