математика. 2020 КЛР8 Математика. Контрольная работа 8 случайные величины и математическая статистика

Название	Контрольная работа 8 случайные величины и математическая статистика
Анкор	математика
Дата	24.01.2023
Размер	140.45 Kb.
Формат файла
Имя файла	2020 КЛР8 Математика.docx
Тип	Контрольная работа #903372

КОНТРОЛЬНАЯ РАБОТА 8 – СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

(1-10) Функция распределения

_F₍_x₎_с_л_у_ча_й_н_о_й_в_е_л_и_ч_и_н_ы__з_а_да_н_а_г_ра_ф_и_ч_ес_к_и_._П_о-

стройте график плотности распределения указанные вероятности.

f( x)

данной случайной величины и найдите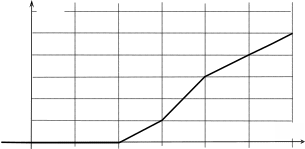

₈_.

^1,²F(x)

₁_,₀
₀_,8
₀_,6
₀_,4

0,2

x
⁰^{1 2}³_{4 5 6}

p₁ P(2    4) ; p₂ P(3  ) ;

p₃ P(  3) .

(11-20) Функция плотности

_f₍_x₎

_с_л_у_ча_й_н_о_й_в_е_л_и_ч_и_н_ы__з_а_да_н_а_г_р_а_ф_и_ч_е_ск_и_._Н_а_йти

математическое ожидание этой случайной величины

_M__и_у_ка_з_а_н_н_ые_в_е_р_о_ятн_о_с_т_и.

18.

^0,⁶_f₍_x₎

_0,₅
₀_,4

₀_,3
₀_,2

0,1

x
⁰^{1 2}3 _{4 5 6}

p P(1    4)

₍₂₁_-₃₀₎_С_л_у_ча_й_на_я_в_е_л_и_ч_и_н_а__,_рас_п_р_е_де_л_е_на_по_н_о_р_м_а_л_ь_н_о_м_у_з_ак_о_н_у_с_п_ара_м_е_т_ра_м_и_a

_и__._Н_а_йти_в_е_р_о_ятн_о_с_т_и_с_о_бы_т_и_й_:

_P₍___A₎_;

_P₍___B₎_;

_P₍_|___a_|__t_₎_.

Номер задачи	28
a	6
	3
_A	2
_B	11
t	0,5

(31-40) Найти доверительный интервал для оценки математического ожидания aнор- мального распределения с надежностью 0,95, зная выборочное среднее x, объем вы- борки nи среднеквадратичное отклонение  .

Номер задачи	38
x	75,11
n	144
^	12

(41-50) В таблицах представлены данные о технико-экономическом показателе X, со- бранные на одной из дорог ОАО «РЖД» за 2010. В результате первичной обработки

данных построен вариационный ряд, проведена группировка, найдены

^x_m_i_n^,

^x_m_a_x

(наименьший и наибольший элементы выборки

^x₁^,^x₂^,^^,^x_n

из генеральной совокуп-

ности X), а также выборочные начальные моменты

₁_n₁_n₂

n
^m₁⁽ⁿ⁾^^ ^x_i^,

i1

^m₂⁽ⁿ⁾^^^ ^x_i

n
i1

, _n_₁₀₀.

_Р_е_з_у_л_ь_т_а_т_ы_г_р_у_п_п_и_р_о_вк_и_с_в_е_д_е_ны_в_т_а_б_л_и_ц_у_,_в_к_о_т_о_р_о_й_k_–_ч_и_с_л_о_и_н_т_е_рва_л_о_в_ра_з_б_и_е-

^н^и^я^о^т^р^е^з^к^а^[^x_m_i_n^,^x_m_a_x^]^,ⁿ_i

– число точек, попавших в i-й интервал i 1, k.

a. Найти размах исходной выборки и числа

^x_m_i_n^,

^x_m_a_x^.

_b_._Н_а_йти_в_ыб_о_р_о_ч_ные_м_о_м_е_нты_д_л_я_в_ыб_о_рк_и,_с_о_с_т_ав_л_е_н_н_о_й_{из п}_е_рв_ых₁₀_э_л_е_м_е_н_т_о_в

^и^с^хо^дн^о^й^в^ыб^о^рк^и,^т^о^е^с^т^ь^ч^и^с^л^а^m₁⁽¹⁰⁾^,

^m₂⁽¹⁰⁾^.

_c_._П_о_г_р_у_п_п_и_р_о_ва_н_н_о_й_в_ыб_о_рк_е_п_о_с_т_р_о_ить_г_и_с_т_ог_ра_м_м_у_о_т_н_о_с_ите_л_ь_ных_час_т_о_т_,

_на_йти_в_ыб_о_р_о_ч_н_о_е_ср_е_дн_е_е_x_и_в_ыб_о_р_о_ч_н_у_{ю ди}_с_п_е_рс_ию

_s²_.

d. Сравнить числа m₁(10) , m₁(100) , xи объяснить их различие.

_e_._Сра_в_н_и_т_ь_г_и_с_т_ог_ра_м_м_у_о_т_н_о_с_ите_л_ь_ных_час_т_о_{т с}_ф_у_н_к_ц_и_е_й_п_л_о_т_н_о_с_т_и_н_о_р_м_а_л_ь_но

распределённой случайной величины с параметрами

a x,   s. Сделать вы-

вод о нормальности генеральной совокупности X, из которой сделана исходная выборка.

(При записи задачи в тетрадь достаточно скопировать лишь группированную выборку.)

Результаты первичной обработки
Номера интервалов	Границы интерва- лов разбиения			Частоты n_i
1	^xmin	83,43	15
2	83,43	101,86	1
3	101,86	120,29	23
4	120,29	138,71	14
5	138,71	157,14	20
6	157,14	175,57	16
7	175,57	^xmax	11
m₁(100)  132,3		m₂(100)  18658

48. Объем перевозки щебня Забайкальской дорогой (в тоннах).

Исходные данные
69 104 137 143 68 74 137 135 142 67	123 109 154 183 176 106 142 177 106 104	104 145 145 140 174 106 172 174 156 134	172 68 140 188 139 102 146 172 173 103	67 139 104 68 67 108 131 107 169 113
105 133 140 68 102 172 147 65 65 173	154 187 178 130 169 139 168 130 101 178	153 103 147 179 146 68 172 176 123 170	151 101 119 130 126 181 166 126 104 194	161 152 104 106 175 135 165 146 116 193