Механика жидкости и газа. Яруков К.А. 24 вариант ГТУ19-1бзу МЖиГ.docx. Контрольная работа Дисциплина Механика жидкости и газа

• Название: Контрольная работа Дисциплина Механика жидкости и газа
• Анкор: Механика жидкости и газа
• Дата: 17.01.2022
• Размер: 1.03 Mb.
• Имя файла: Яруков К.А. 24 вариант ГТУ19-1бзу МЖиГ.docx.doc
• Тип: Контрольная работа; #333970

Министерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное учреждение
высшего образования

«Пермский национальный исследовательский
политехнический университет»
Кафедра «Ракетно-космическая техника и энергетические системы»

Контрольная работа

Дисциплина

«Механика жидкости и газа»

Вариант 24

Выполнил: студент гр. ГТУ-19-1бзу:

Яруков К.А.

г. Пермь 2021

Задача 1

Пластина площадью S движется со скоростью u₀ = 0,3 м/с параллельно неподвижной горизонтальной плоскости 0-0, образуя с ней зазор b = 8 мм. Принять линейный закон изменения скорости по сечению зазора Динамическая вязкость жидкости μ = 0,24 Па·с, площадь пластины S = 0,1 м². Определить силу вязкого трения Т и касательное напряжение τ в жидкости на поверхности соприкосновения с пластиной.

Найти: Т, τ - ?.

Решение:

По закону Ньютона сила вязкого трения равна:

Т = τ·S,

где 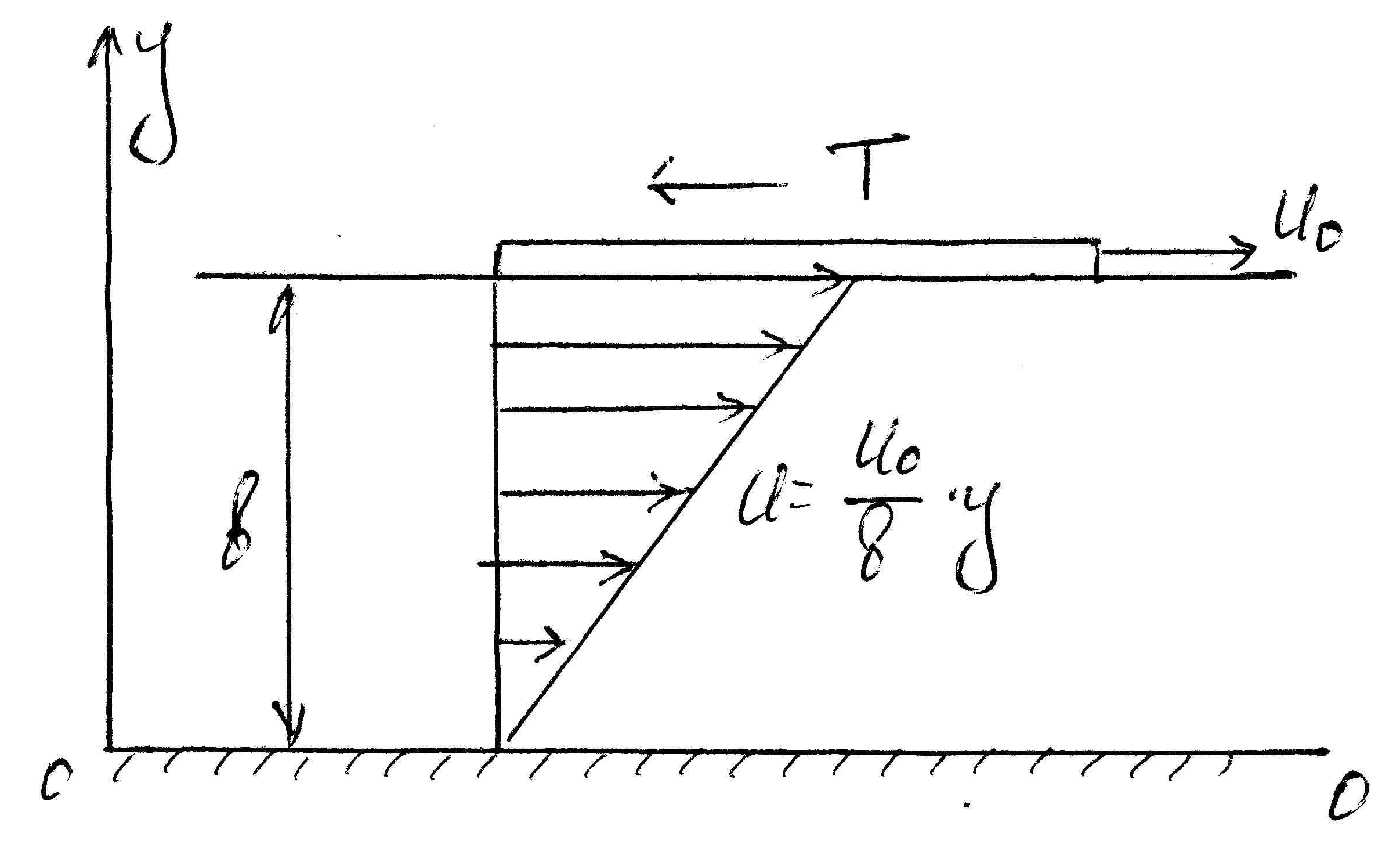- касательное напряжение в жидкости на поверхности соприкосновения с пластиной; μ - динамическая вязкость жидкости; S -площадь пластины; - градиент скорости.



Таким образом,





Ответ:

Задача 2. Определить абсолютное давление воздуха в сосуде р_b при следующих исходных данных: плотность ртути ρ_рт = 13600 кг/м³; плотность воды ρ_в = 1000 кг/м³; атмосферное давление р_а = 736 мм.рт.ст. = 97,9 кПа; h = 450 мм; Н = 0,7 м.

Найти: р_b - ?.

Решение:

Давление в точках А и В, принадлежащих одной поверхности уровня, одинаково:

р_А = р_В,

где р_А = р_а; р_А = ρ_ртgh + ρ_вgН + р_b; ρ_в – плотность жидкости; р_b – абсолютное давление воздуха в сосуде.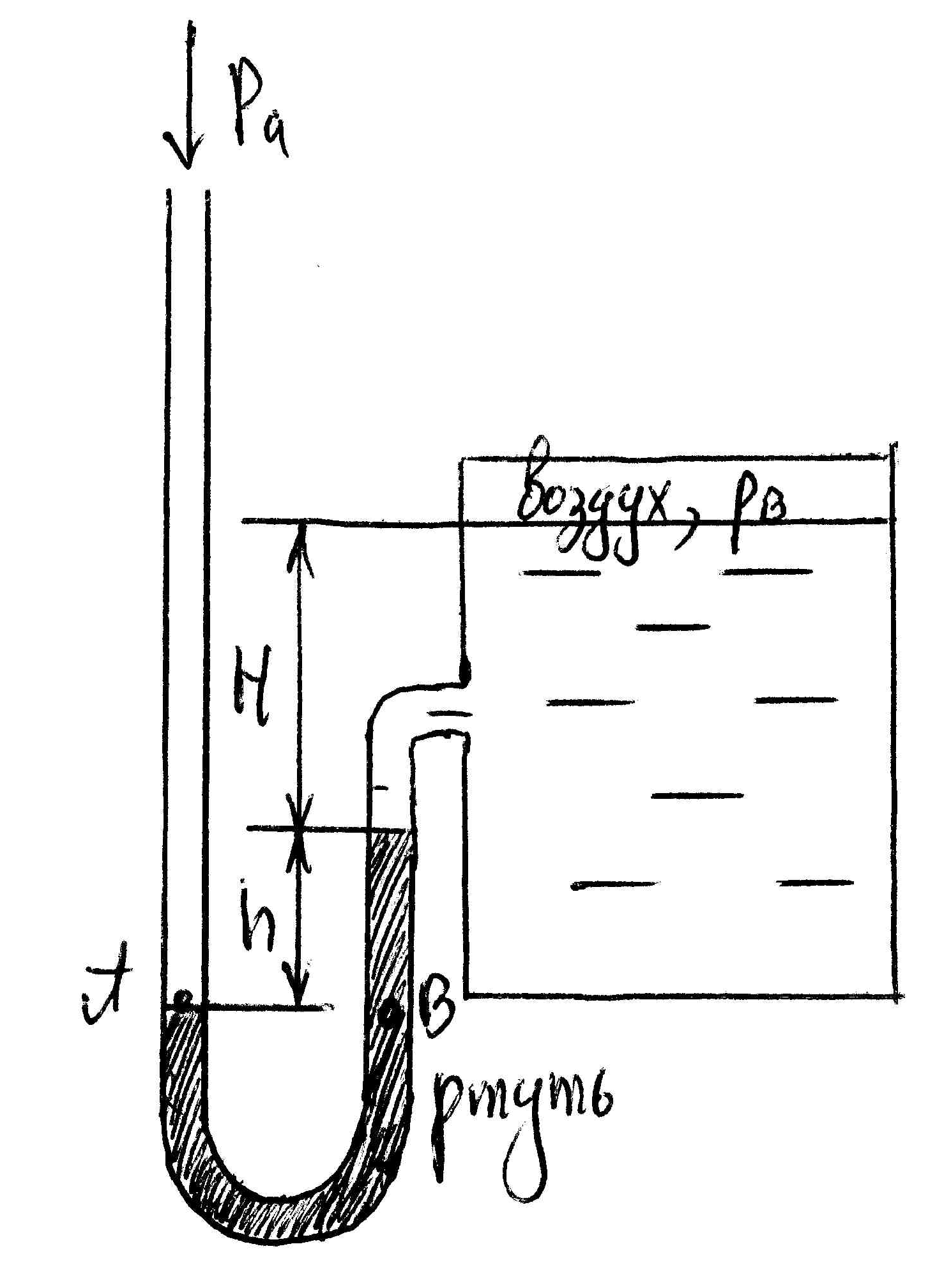



Таким образом,

р_а = ρ_ртgh + ρ_вgН + р_b;

р_b = р_а – g(ρ_ртh + ρ_вН) = 97,9·10³ – 9,81·(13600·0,450 + 1000·0,7) = 31,0 кПа.

Ответ: р_b = 31,0 кПа.

Задача 3. Определить силу давления воды на крышку люка. Диаметр люка 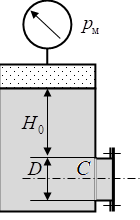= 1,5 м, высота = 4,0 м. Показания манометра .



Найти: F - ?.

Решение:

Абсолютное давление в центре С крышки люка слева равно:



где - расстояние от свободной поверхности жидкости до точки С; р_а – атмосферное давление.

Площадь крышки люка равна:



Сила давления жидкости на крышку люка равна:

_{F = (pc– pa) Sл =}





Ответ: _{F = 223,6 кН.}

Задача 4. Определить показания мановакуумметра 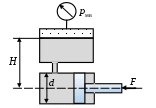, если к штоку приложена сила = 0,40 кН, его диаметр = 140 мм, высота , плотность .



Решение.

Искомая величина давления р определяется из равенства силы давления на поршень со стороны жидкости и силы приложенной к штоку.



Отсюда,

14,2 кПа.

Ответ: 14,2 кПа.

Задача 5. Напорный трубопровод имеет прямоугольное сечение со сторонами 0,14 м и = 0,20 м. Средняя в сечении скорость . Кинематическая вязкость жидкости . Определить режим движения жидкости.

Решение:

Для определения числа Рейнольдса для труб некруглого сечения воспользуемся формулой:



где v – средняя в сечении скорость потока; d = 4R – эквивалентный диаметр некруглой трубы; 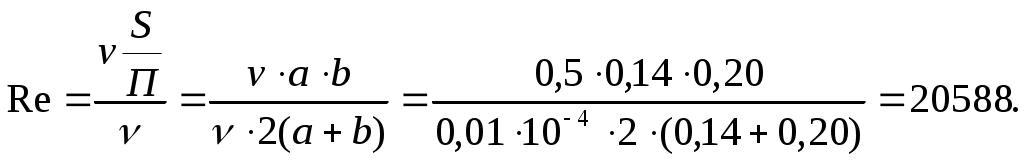- гидравлический радиус; S = a·b – площадь поперечного сечения трубопровода; - смоченный периметр поперечного сечения трубопровода; - кинематический коэффициент вязкости.



Критическое значение числа Рейнольдса для некруглого сечения равно Re_кр = 2320.

Так как Re > Re_кр, то режим движения турбулентный.

Ответ: режим движения турбулентный