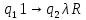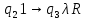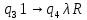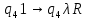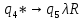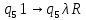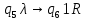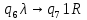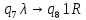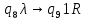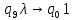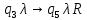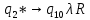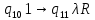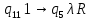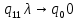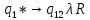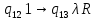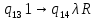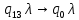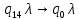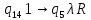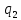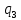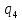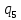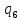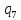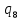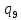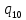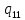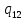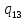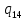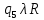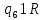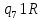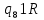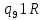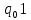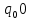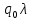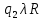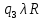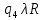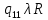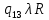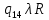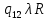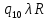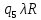Математическая логика. Контрольная работа для заочников
 Скачать 7.85 Mb. Скачать 7.85 Mb.
|
Контрольная работа для заочниковпо математической логике и теории алгоритмов Вариант 30  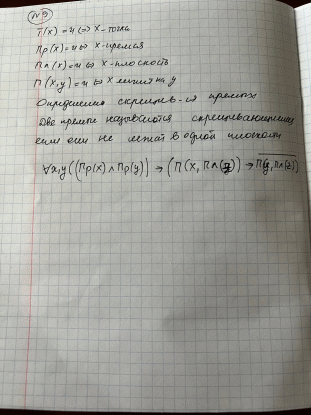 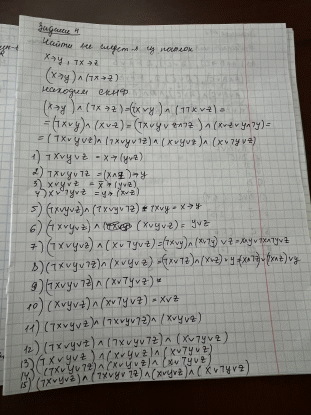  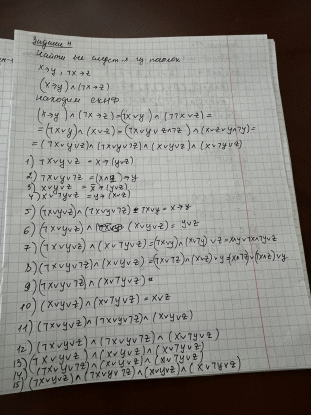 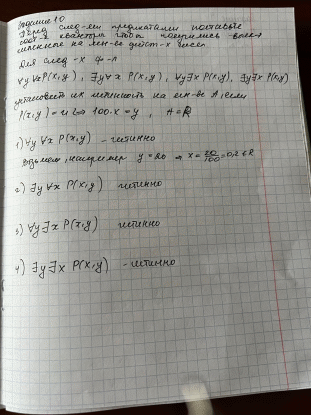  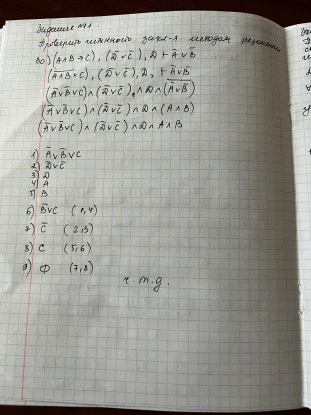   Задание 12Свести к предложениям (множествам дизъюнктов) следующие формулы; выполнить унификацию дизъюнктов. 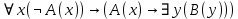 Решение 1).Преобразуем формулу, применяя законы логики предикатов: 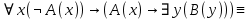 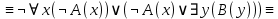 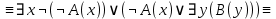 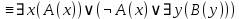 Т.к. в подформуле 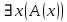 переменная х связанна, в подформуле переменная х связанна, в подформуле 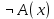 – свободная, заменим во второй подформуле переменную х на переменную t: – свободная, заменим во второй подформуле переменную х на переменную t: 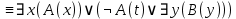 Вынесем вперед кванторы: 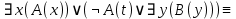 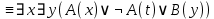 Избавимся от кванторов существования, заменяя переменные х и у на константы: 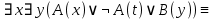 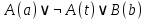 Множество дизъюнктов состоит из одного дизъюнкта: 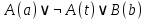 2) Т.к. множество дизъюнктов состоит из одного дизъюнкта, унификация не проводится. Ответ: 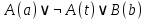 . .Задание 13Найти функцию f(x,y), полученную из функций g(x) и h(x, у, z) по схеме примитивной рекурсии. g(x)= 0 h(x,y,z)= x – y+z Решение Запишем схему примитивной рекурсии 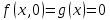 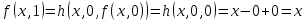 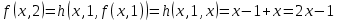 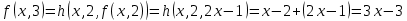 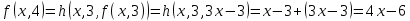 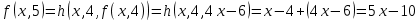 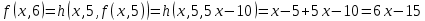 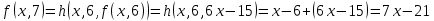 … 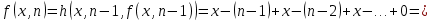 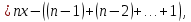 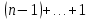 – сумма арифметической прогрессии с – сумма арифметической прогрессии с 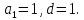 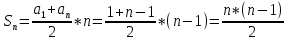 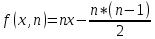 Таким образом 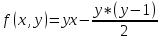 Ответ:  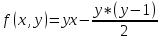  Задание 14 Построить машину Тьюринга, вычисляющую числовую функцию f(x1,x2,…,xn); Проверить работу построенной машины над некоторыми наборами значений переменных. Решение Пусть числа х и у записаны на ленте в виде массивов из х и у единиц, разделенных *. Необходимо проверить условие: если сумма единиц в двух массивах больше 4-х, то необходимо на ленте оставить 6 единиц, в противном случае – стереть оба массива. Пусть машина начинает работу с первой непустой ячейки слева, с состояния 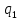 . .
Проверим работу МТ на слове 1*1, т.е. вычислим f(1,1). Запишем полученные конфигурации 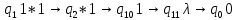 Выходное слово: 0, f(1,1)=0. Проверим работу МТ на слове 111*1, т.е. вычислим f(3,1). Запишем полученные конфигурации 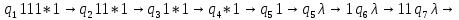 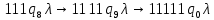 Выходное слово: 11111, f(3,1)=5. Запишем в таблице команды МТ.
Ответ:
|