Главная страница
Навигация по странице:

  • Контрольная работа по алгебре за III четверть. 8 класс. Вариант II

  • Контрольная работа по алгебре за III четверть. 8 класс. Вариант III

  • Контрольная работа по алгебре за III четверть. 8 класс. Вариант IV Часть 11. Укажите верное утверждение:1) Если D =0

    		•

    Контрольная работа по алгебре за 3 четверть, 8 класс. Контрольная работа по алгебре за iii четверть. 8 класс


    Скачать 112 Kb.
    НазваниеКонтрольная работа по алгебре за iii четверть. 8 класс
    Дата24.04.2023
    Размер112 Kb.
    Формат файлаdoc
    Имя файлаКонтрольная работа по алгебре за 3 четверть, 8 класс.doc
    ТипКонтрольная работа
    #1084991

    Контрольная работа по алгебре за III четверть. 8 класс.
    Вариант I

    Часть 1

    1. Укажите верное утверждение:

    1) Уравнение, приводимое к виду ах2+вх+с=0, где а,в,с некоторые числа, х- переменная, причем а≠0, называется линейным уравнением.

    2) Уравнение, приводимое к виду ах2+вх+с=0, где а,в,с некоторые числа, х- переменная, причем а≠0, называется квадратным уравнением.

    3) Уравнение, приводимое к виду ах2+вх+с=0, где а,в,с некоторые числа, х- переменная, причем а≠0, называется дробно-рациональным уравнением.
    2. Какие из чисел являются корнями уравнения х2 + 2х – 3 = 0.

    1) 1; -3 2) –1; 3 3) нет таких чисел. 4) 0; 4
    3. Найдите дискриминант квадратного уравнения 5х2 – 4х – 1 = 0.

    1) 16 2)- 20 3) 36 4)16
    4. Найдите наибольший корень уравнения 2х2 + 3х – 5 = 0.

    1) –2,5 2) 1 3) –1 4) 2,5
    5. Решите уравнение х2 – х = 0.

    1) 0; 1 2) –1; 1 3) 0 4) 0; -1
    Часть 2
    6. Решите уравнение (х + 1) 2 = 7х – 3х2
    7. Один из корней квадратного уравнения х2 + 5х + q = 0 равен – 2. Найдите второй корень уравнения и коэффициент q.

    Часть 3




    8. Решите уравнение

    9. Решите задачу

    Контрольная работа по алгебре за III четверть. 8 класс.

    Вариант II

    Часть 1

    1. Укажите верное утверждение:

    1) Квадратное уравнение, у которого коэффициент а=1, называется приведенным.

    2) Квадратное уравнение, у которого коэффициент а=1, называется неприведенным.

    3) Квадратное уравнение, у которого коэффициент а=1, называется неполным.
    2. Какие из чисел являются корнями уравнения 2х2 + 5х – 3 = 0.

    1) 3; 0,5 2) –0,5; -3 3) 0,5; -3 4) 1; 0
    3. Найдите дискриминант квадратного уравнения х2 – 6х + 9 = 0.

    1) 2 2) 9 3) 0 4) 36
    4. Найдите наибольший корень уравнения 5х2 – 7х + 2 = 0.

    1) 0,4 2) 1 3) –1 4) 2
    5. Решите уравнение 7х - 4 х2 = 0

    1) 0; - 1,75 2)1,4; 1,75 3) –3; 0 4) 0; 1,75

    Часть 2
    6. Решите уравнение (х + 3) 2 = 2х + 6
    7. Один из корней квадратного уравнения х2 +pх – 16 = 0 равен – 2. Найдите второй корень уравнения и коэффициент p.

    Часть 3




    8. Решите уравнение

    9. Решите задачу

    Контрольная работа по алгебре за III четверть. 8 класс.


    Вариант III

    Часть1

    1. Укажите верное утверждение:

    1) Формула дискриминанта: D= в– 4ас

    2) Формула дискриминанта: D= в2- 4а

    3) Формула дискриминанта: D= в2- 4аc
    2. Какие из чисел являются корнями уравнения 6х2 + х = 0.

    1) нет таких чисел 2) 0; 3) 0; 1 4) 2; 0
    3. Найдите дискриминант квадратного уравнения 3х – х2 + 10 = 0.

    1) 49 2) - 49 3) 9 4) 25
    4. Найдите наибольший корень уравнения 3х2 + 5х – 2 = 0.

    1) 2 2) 3) 4) 4

    5. Решите уравнение х2 + 5х + 6 = 0.

    1) - 2; - 3 2) 2; 3 3) 3; 0 4) 2; -3

    Часть 2
    6. Решите уравнение (х – 2) 2 = 3х – 8
    7. Один из корней квадратного уравнения х2– 5х + q = 0 равен – 3. Найдите второй корень уравнения и коэффициент q.

    Часть 3




    8. Решите уравнение

    9. Решите задачу
    Турист проехал на моторной лодке против течения 25 км, а обратно спустился на плоту. В лодке он плыл на 10 ч меньше, чем на плоту. Найдите скорость течения, если скорость лодки в стоячей воде 12 км/ч.


    Контрольная работа по алгебре за III четверть. 8 класс.
    Вариант IV

    Часть 1

    1. Укажите верное утверждение:

    1) Если D=0, то уравнение имеет один корень.

    2) Если D=0, то уравнение имеет два корня

    3) Если D=0, то уравнение не имеет корней
    2. Какие из чисел являются корнями уравнения 6х2 –5х – 1 = 0

    1) –3; 2 2) 2; 4,2 3) 1; 4) - 2; 0
    3. Найдите дискриминант квадратного уравнения 2х + 3 + 2х2 = 0.

    1) 20 2) 10 3) 15 4) - 20
    4. Найдите наибольший корень уравнения 5х2 – 8х + 3 = 0.

    1) – 0,6 2) 0,5 3) 1 4) -1

    5. Решите уравнение 5х2 + 8х - 4 = 0.

    1) 0,5; 2 2) 0,4; - 2 3) 0,5; 1 4) нет решений
    Часть 2
    6. Решите уравнение (х – 1) 2 = 29 – 5х
    7. Один из корней квадратного уравнения х2+ pх +18 = 0 равен – 3. Найдите второй корень уравнения и коэффициент p.

    Часть 3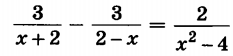




    8. Решите уравнение

    9. Решите задачу

    Катер прошел 80 км по течению реки и вернулся обратно, затратив на весь путь 9 часов. Найдите собственную скорость катера, если скорость течения реки 2 км/ч.

    Критерии оценивания

    5 – 8 баллов – оценка «3»

    9 – 14 баллов – оценка «4»

    15 – 16 баллов – оценка «5»

    № задания
    1
    2
    3
    4
    5
    6
    7
    8
    9

    балл
    1
    1
    1
    1
    1
    2
    2
    3
    4


    Ответы

    1 вариант

    № задания
    1
    2
    3
    4
    5
    6
    7

    Ответ

    2
    1
    3
    2
    1
    0,25; 1
    Х= - 3

    q= 6


    Ответы

    2 вариант

    № задания
    1
    2
    3
    4
    5
    6
    7

    Ответ

    1
    3
    3
    2
    4

    • 3;

    • 1
    Х=8;

    P = - 6


    Ответы

    3 вариант

    № задания
    1
    2
    3
    4
    5
    6
    7

    Ответ

    3
    2
    1
    3
    1
    3; 4
    Х=8;

    P = - 24


    Ответы

    4 вариант

    № задания
    1
    2
    3
    4
    5
    6
    7

    Ответ

    1
    3
    4
    3
    2
    -6; 3
    Х= - 6;

    P = 9

    написать администратору сайта