автоматика контрольная работа №1 Кадыров. Контрольная работа по дисциплине автоматизированные системы нефтегазового производства Вариант 23
 Скачать 158.31 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВПО «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ НЕФТИ И ГАЗА ИМ. М.С. ГУЦЕРИЕВА КАФЕДРА РАЗРАБОТКИ И ЭКСПЛУАТАЦИИ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ Контрольная работа по дисциплине «АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ НЕФТЕГАЗОВОГО ПРОИЗВОДСТВА» Вариант 23 Выполнил: студент 3 курса группа ЗССПБ-21.03.01.31(К)Э Кадыров Тимур Ильдарович Проверил: преп-ль Ларионов Константин Игоревич ИЖЕВСК 2020. Задача №1. Форма дифференциального уравнения: AD1 + BD2 + CD3 = EG1 + FG2 где A,B,C,E,F – коэффициенты, D1,D2,D3 – функции левой части уравнения, G1,G2 - функции результирующего сигнала. Значения коэффициентов и производных выбираются по табл. 1. Дано: А=3,В=1,С=1,Е=0,F=1, D1= x’’, D2= x’, D3= x, G1= g’’, G2=g Решение: По индивидуальному варианту записываем дифференциальное уравнение. Пусть уравнение имеет вид: 3 x’’+ x’+x=g при граничных и начальных условиях: x’(0) = x’0, x(0) = x0. Разрешим уравнение относительно члена со старшей производной: 3 x’’=g- x’-x Изобразим схему получения сигнала 3x’’. Для этого подадим его на усилительное звено с коэффициентом усиления 1/3 и получим сигнал x’.   1/3 3х’’ x’’   Проинтегрируем дважды сигнал x’’ и применим граничные и начальные условия через суммирующие элементы: 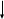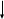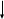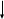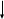x’0 x0    + 1/p + 1/p 1/3 3x’’ x’’ x’ x   1/p + 1/p 1/p + 1/p 1/p + 1/p 1/p + 1/p 1/4 1/4 Установим слева от полученной схемы главный сумматор и подадим на него составляющие сигнала с x’ и х:  + 1/p + 1/p 1/3 + + + 3x’’ x’’ x’0 x’ x0 x’ x     _ _  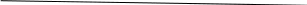 Эта часть структурной схемы соответствует правой части уравнения Соединим два фрагмента: + + g 3x’’ x’ x’0 x0 1/p + 1/p 1/3 x’ x _ _ 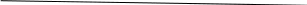Задача решена. Задача №2. Структурная схема   В + А g x   С где A,B – операторы, С – коэффициент усиления обратной связи. Дано: А=1/3p, B=1/2, С=2 Обозначим на схеме входной сигнал g и выходной сигнал х. Обозначим недостающие сигналы и пронумеруем звенья: 4 1 2   1/3p 1/2 + g ɛ x 3 2 Составим уравнения звеньев относительно выходного сигнала: X=(1/3p)* ɛ X=(1/2)* ɛ X=(2)* ɛ ɛ=g-x Решаем полученную систему из двух уравнений в операторном виде: х =1/3р(g – x); 3рх = g – x; (3p + 1) x = g. х =1/2(g – x); 2х = g – x; 3 x = g. х =2(g – x); х = g – x; x = g. Преобразуем полученное в операторном виде уравнение к дифференциальному виду: x’(t) + x(t) = g(t). x’(t) + x(t) = g(t). x’(t) + x(t) = g(t). Задача решена. |