контрольная по физике 2 курс. Контрольная работа По дисциплине Биофизика Вариант студент заочного обучения
 Скачать 119.99 Kb. Скачать 119.99 Kb.
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ имени А.А. ЕЖЕВСКОГО Факультет энергетический Кафедра электрооборудования и физики Контрольная работаПо дисциплине «Биофизика» Вариант ____ Выполнил: студент заочного обучения направления подготовки __________профиль__________________________ курс______________________________ группа____________________________ ФИО_____________________________ Проверил:_________________________ Молодежный, 2023 г.108. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 100 м. Закон движения автомобиля выражается уравнением 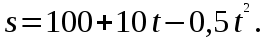 Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой секунды. Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в конце пятой секунды.Решение: найдем скорость, вычислив производную от уравнения движения. 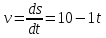 Подставим значение, равное 5 сек, получим 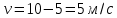 Тангенциальное ускорение найдем, взяв производную от полученного ранее уравнения скорости: 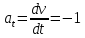 . Видим, что тангенциальное ускорение . Видим, что тангенциальное ускорение 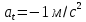 Нормальное ускорение определяется по формуле 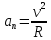 . Подставим найденное значение скорости и значение радиуса по условию, получим: . Подставим найденное значение скорости и значение радиуса по условию, получим: 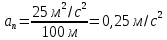 Полное ускорение найдем по формуле: 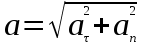 . .Получим 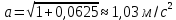 118. Человек массой 70 кг, бегущий со скоростью 9 км/ч, догонят тележку массой 190 кг, движущуюся со скоростью 3,6 км/ч, и вскакивает на нее. С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке? Решение: чтобы найти необходимую скорость воспользуемся законом сохранения импульса: 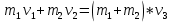 , где , где 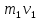 - импульс человека до удара, - импульс человека до удара, 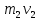 - импульс вагона до прыжка, - импульс вагона до прыжка, 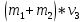 - общий импульс человека и вагона после прыжка. - общий импульс человека и вагона после прыжка.Так как вагон движется в сторону человека, то, проектирую вектора импульсов на ось X, получаем: 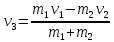 Подставим числа, получим: 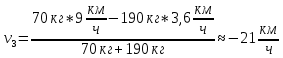 Получили отрицательное число, что говорит нам о том, что вагон с человеком продолжили движение в сторону движения вагона, итоговый ответ: 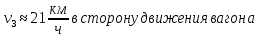 128. Спутник вращается вокруг Земли по круговой орбите радиусом 1700 км. Определить его линейную скорость и период обращения, если радиус Земли равен 6400 км. Решение: воспользуемся формулой для вычисления первой космической скорости: 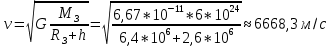 Период обращения вычислим по формуле: 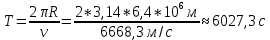 138. Вычислить кинетическую энергию вала диаметром 0,3 м, вращающегося с частотой 200 об/мин, если масса его 2·103 кг. Решение: кинетическая энергия вращающегося тела относительно неподвижной оси равна 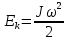 , момент инерции сплошного цилиндра , момент инерции сплошного цилиндра 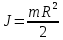 , угловая частота , угловая частота 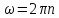 , где n – число оборотов в секунду, также имеем , где n – число оборотов в секунду, также имеем 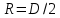 , получим расчетную формулу: , получим расчетную формулу: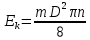 Найдем число оборотов в секунду: 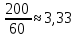 Вычислим кинетическую энергию, получим 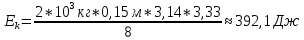 148. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению 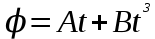 , где А = 2 рад/с, В = 0,2 рад/с3. Определить вращающий момент, действующий на стержень через 2 с после начала вращения, если момент инерции стержня , где А = 2 рад/с, В = 0,2 рад/с3. Определить вращающий момент, действующий на стержень через 2 с после начала вращения, если момент инерции стержня 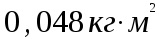 . .Решение: Из второго закона Ньютона к вращающимся телам находим 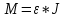 , где M – вращающийся момент, , где M – вращающийся момент, 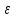 – угловое ускорение, J – момент инерции диска. – угловое ускорение, J – момент инерции диска.По определению 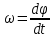 , тогда , тогда 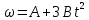 , а , а 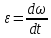 , тогда , тогда 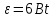 . .В момент времени t = 2, имеем, что 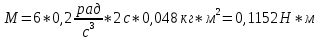 158. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых 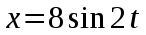 и и 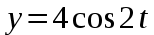 . Написать уравнение траектории и построить ее. Показать направление движения точки. . Написать уравнение траектории и построить ее. Показать направление движения точки.Решение: параметрическое уравнение эллипса выглядит следующим образом 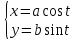 Где a и b – длина полуоси эллипса, в таком случае имеем аналогичное уравнение траектории: 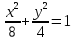 От 2t в данном случае зависит лишь период обращения, в нашем случае период равен 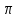 . . 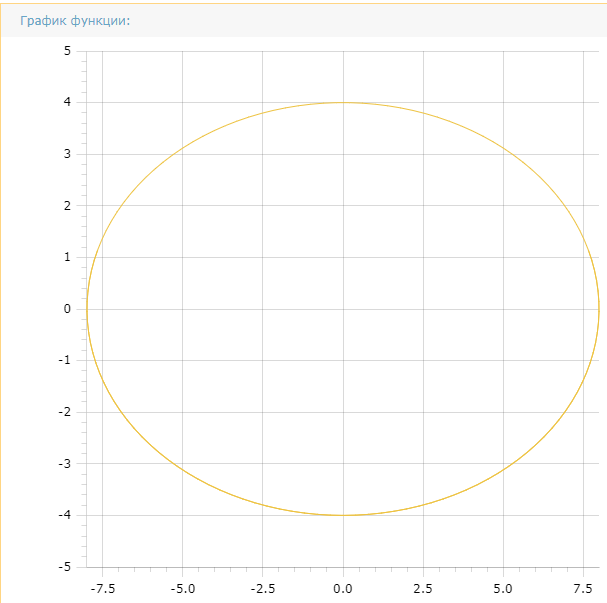 Для определения направления движения, возьмем момент времени t = 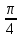 , имеем, что , имеем, что 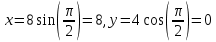 , учитывая, что в при t = 0, имеем x = 0, а y = 4, заключаем, что движение идет по часовой стрелке. , учитывая, что в при t = 0, имеем x = 0, а y = 4, заключаем, что движение идет по часовой стрелке.208. Вычислить плотность азота, находящегося в баллоне под давлением 2 МПа и имеющего температуру 400 К. Решение: воспользуемся уравнением Менделеева-Клапейрона, т.к. плотность определяется как 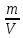 , выразим это из формулы: , выразим это из формулы: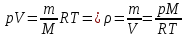 Подставим значения, получим 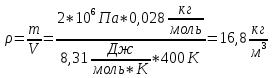 218. Давление идеального газа 10 мПа, концентрация молекул 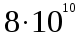 см-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа. см-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа.Решение: для начала найдем температуру, используя формулу зависимости давления газа от концентрации и температуры: 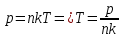 После этого найдем среднюю кинетическую энергию одной молекулы идеального газа по формуле: 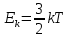 Подставим значения, получим: 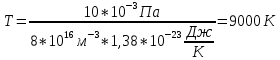 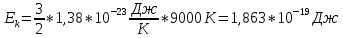 При решении также пользовались 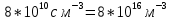 228. Средняя квадратичная скорость некоторого газа при нормальных условиях равна 480 м/с. Сколько молекул содержит 1 г этого газа? Решение: при нормальных условиях, значит 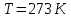 , тогда, воспользуемся формулой средней квадратичной скорости, чтобы найти молярную массу: , тогда, воспользуемся формулой средней квадратичной скорости, чтобы найти молярную массу: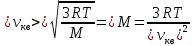 Тогда количество молекул в грамме этого газа будет находиться по формуле: 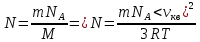 Подставим значения, получим 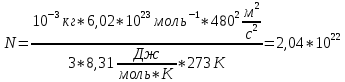 238. Найти молярную массу среды, для которой удельная изобарная теплоемкость сp = 1820 Дж/( 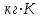 ) и изохорная cv = 1360 Дж/( ) и изохорная cv = 1360 Дж/(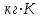 ). ).Решение: молярная теплоемкость газа при постоянном объеме равна 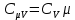 , аналогично при постоянном давлении , аналогично при постоянном давлении 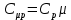 Запишем уравнение Майера: 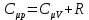 Таким образом можем выразить молярную массу, получим: 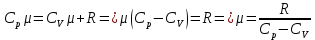 Подставим значения, получим: 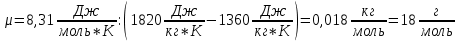 248. Водород массой 4 г был нагрет на 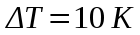 при постоянном давлении. Определить работу расширения газа. при постоянном давлении. Определить работу расширения газа.Решение: работа при изобарном расширении определяется по формуле: 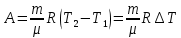 Подставим значения, получим: 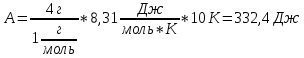 258. Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Определить: 1) термический КПД цикла; 2) отношение температур нагревателя и холодильника. Решение: термический КПД цикла определим по формуле: 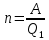 Определим отношение температур, исходя из формулы: 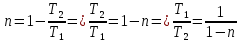 Подставим значения: 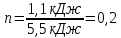 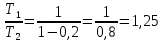 Расстояние l между зарядами Q  нКл равно 25 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r1 = 15 см от первого и на расстоянии r2 = 20 см от второго заряда. нКл равно 25 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r1 = 15 см от первого и на расстоянии r2 = 20 см от второго заряда.Решение: покажем на рисунке. 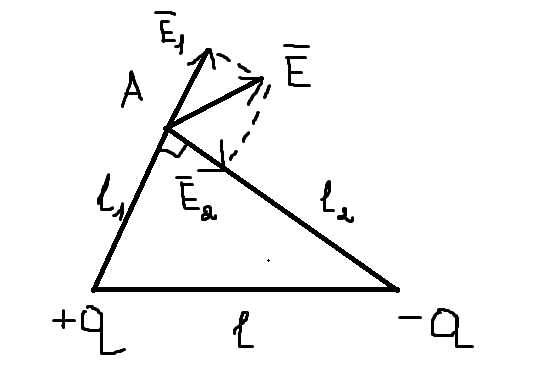 По принципу суперпозиции имеем, что напряженность поля есть сумма векторов E1 и E2, т.е. на рисунке это вектор E, найдем его с помощью теоремы Пифагора: 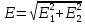 Каждый вектор найдем по формулам: 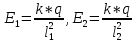 Подставим формулы, получим: 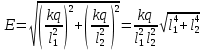 Подставим значения, получим: 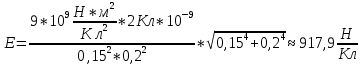 318. Пылинка массой 0,2 мг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость 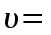 10 м/с. Определить скорость 10 м/с. Определить скорость 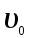 пылинки до того, как она влетела в поле. пылинки до того, как она влетела в поле.Решение: из закона сохранения энергии имеем: 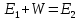 Где 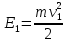 - начальная кинетическая энергия пылинки, - начальная кинетическая энергия пылинки, 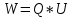 – потенциальная энергия пылинки, проходящей через разность потенциалов U, – потенциальная энергия пылинки, проходящей через разность потенциалов U, 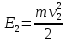 – конечная кинетическая энергия пылинки. – конечная кинетическая энергия пылинки. Значит имеем, что 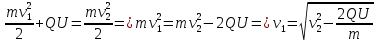 Подставим значения, получим: 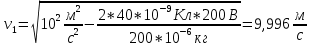 328. Плоский воздушный конденсатор заряжен до разности потенциалов 300 В. Площадь пластин S = 1см2, напряженность поля в зазоре между ними Е = 300 кВ/м. Определить поверхностную плотность заряда на пластинах, емкость и энергию конденсатора. Решение: Напряженность E поля в зазоре между обкладками конденсатора определяется по формулам: 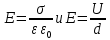 Отсюда, 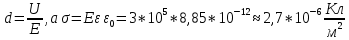 Диэлектрическую проницаемость воздуха взяли равной единице. Емкость конденсатора найдем по формуле: 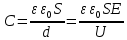 Подставим значения, 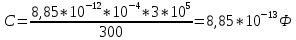 Энергию конденсатора найдем по формуле: 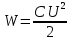 Подставим значения: 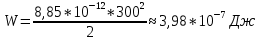 338. Определить плотность тока в железном проводнике длиной 10 м, если провод находится под напряжением 6 В, удельное сопротивление железа 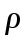 = 98 нОм·м. = 98 нОм·м.Решение: сила тока определяется по формуле 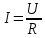 , где , где 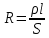 , выразим плотность тока. , выразим плотность тока.Плотность тока определим по формуле: 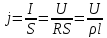 Подставим значения: 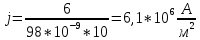 338. ЭДС батареи аккумуляторов равна 12 В, сила тока короткого замыкания равна 5 А. Какую наибольшую мощность можно получить во внешней цепи, соединенной с такой батареей? Решение: полезная мощность, которая выделяется на внешней цепи, можно найти по формуле 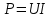 , где U – напряжение на внешней цепи, можно найти согласно закону Ома по формуле , где U – напряжение на внешней цепи, можно найти согласно закону Ома по формуле 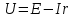 . .Подставим последнюю формулу напряжения в формулу мощности, получим 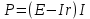 , таким образом рассмотрим теперь функцию мощности, которая зависит от силы тока: , таким образом рассмотрим теперь функцию мощности, которая зависит от силы тока: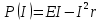 Как видим, данная функцию является параболой, ветви которой направлены вниз, значит её максимум достигается в экстремуме, найдем производную и вычислим значение максимума: 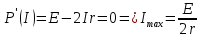 Также знаем, что 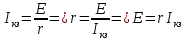 , где E – ЭДС источника, а r – внутреннее сопротивление. , где E – ЭДС источника, а r – внутреннее сопротивление.Получили 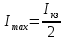 , подставим данное значение в функцию мощности, получим, , подставим данное значение в функцию мощности, получим,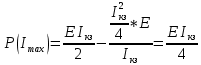 Подставим значения и получим ответ: 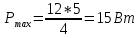 408. По кольцевому медному проводнику протекает ток 30 А. В центре контура с током создается магнитное поле напряженностью 30 А/м. Определить разность потенциалов на концах проводника, если его поперечное сечение 3 мм2. Удельное сопротивление меди 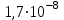 Ом·м. Ом·м.Решение: напряженность магнитного поля в центре кольца определяется формулой 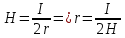 Разность потенциалов 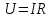 , где , где 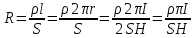 Таким образом выразим, 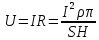 Подставим значения и вычислим, 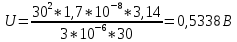 418. Контур из провода, изогнутого в форме квадрата со стороной а = 0,5м, расположен в одной плоскости с бесконечным прямолинейным проводом с током I = 5 А так, что две его стороны параллельны проводу. Сила тока в контуре I1 = 1 А. Определить силу, действующую на контур, если ближайшая к проводу сторона контура находится на расстоянии b = 10 см. Решение: покажем на рисунке контур и направление токов. 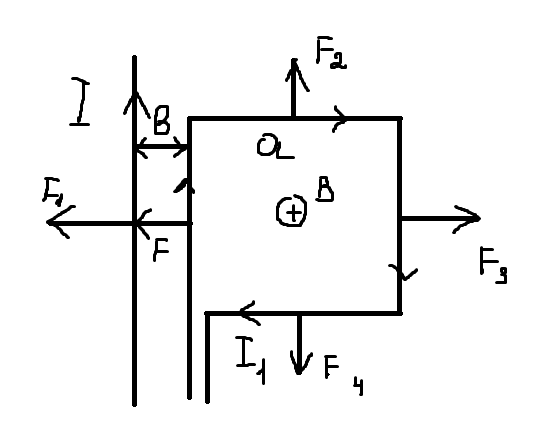 Таким образом видим, что 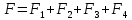 , но т.к. , но т.к. 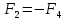 , имеем, что , имеем, что 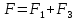 , перейдем из векторного вида, получим, что , перейдем из векторного вида, получим, что 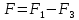 Учитывая, что 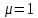 , имеем, что , имеем, что 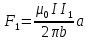 , а , а 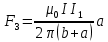 , тогда получим в итоге , тогда получим в итоге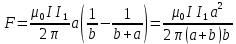 Подставим значения и получим, 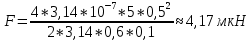 428. В плоскости, перпендикулярной однородному магнитному полю напряженностью 2·105 А/м вращается стержень длиной 0,4 м относительно оси, проходящей через его середину. В стержне индуцируется электродвижущая сила, равная 0,2 В. Определить угловую скорость стержня. Решение: связь линейной и угловой скорости определяется следующим соотношением 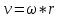 Стержень вращается относительно оси, проходящей через его середину, а значит у разных точек стержня разные радиусы вращения, и следовательно, разная линейная скорость, но, как видим из формулы, скорость линейно зависит от расстояния, потому для нахождения ЭДС возникающей в стержне будем использовать среднюю линейную скорость 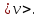 Тогда 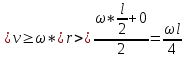 Связь между индукцией и напряженностью магнитного поля 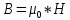 ЭДС 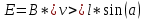 Подставим формулу индукции и средней скорости в формулу ЭДС, получим 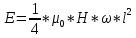 Учитывая, что плоскость вращения стержня перпендикулярна линиям магнитной индукции, то имеем что 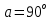 , а , а 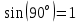 Выразим угловую скорость стержня: 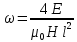 Подставим значения, 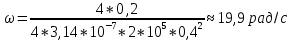 438. На дифракционную решетку, содержащую 500 штрихов на 1 мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину спектра первого порядка на экране, если расстояние L от линзы до экрана равно 3 м. Границы видимого спектра λкр. = 780 нм, λф = 400 нм. Решение: 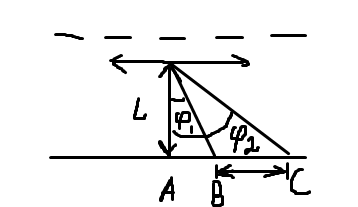 как знаем, 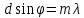 , в нашем случае нужно определить ширину спектра первого порядка и потому , в нашем случае нужно определить ширину спектра первого порядка и потому 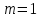 , значит имеем, , значит имеем,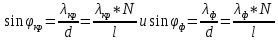 Имеем, что 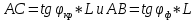 Итого имеем формулу: 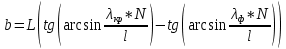 Подставим значения в формулу и решим, 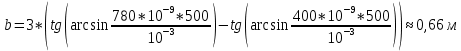 448. На поверхность металла падает монохроматический свет с длиной волны 0,1 мкм. Красная граница фотоэффекта 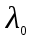 = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?Решение: Формула Эйнштейна для фотоэффекта 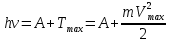 , где , где 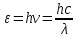 – энергия фотона. – энергия фотона. Откуда видим, что 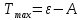 Если V=0, то 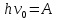 , где , где 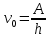 - красная граница фотоэффекта. - красная граница фотоэффекта.По определению 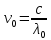 , где c – скорость ветра, тогда , где c – скорость ветра, тогда 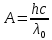 – работа выхода из металла. – работа выхода из металла.Тогда 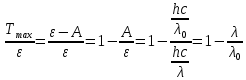 Подставим значения и получим, 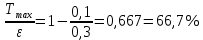 458. Постоянная радиоактивного распада 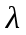 для изотопа для изотопа 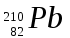 равна 10-9 с-1. Определить время, в течение которого распадается 2/5 начального количества ядер этого радиоактивного изотопа. равна 10-9 с-1. Определить время, в течение которого распадается 2/5 начального количества ядер этого радиоактивного изотопа.Решение: 2/5 начального количества ядер радиоактивного изотопа распалось, значит осталось 3/5, запишем 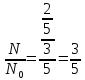 Запишем закон радиоактивного распада: 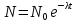 Где λ – постоянная радиоактивного распада. Выразим t: 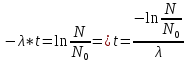 Подставим значения, получим 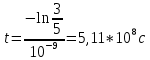 468. Вычислить энергию ядерной реакции 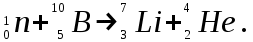 Решение: Энергия ядерной реакции определяется по формуле: 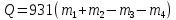 Вычислим массу ядер до реакции и после реакции, До реакции имеем: 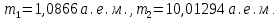 После реакции имеем: 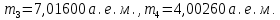 Подставим все значения и вычислим энергию: 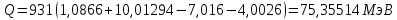 |
