КР вариант 1. Контрольная работа по дисциплине EH. 01 Математика Вариант 1 Специальность 26. 02. 02 Судостроение Студент группы зскм12
 Скачать 183.42 Kb. Скачать 183.42 Kb.
|
|
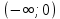 | 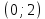 | 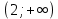 |
| y'>0 | y'<0 | y'>0 |
| возрастает | убывает | возрастает |
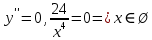
Точек перегиба нет.
Асимптоты:
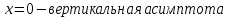
График:
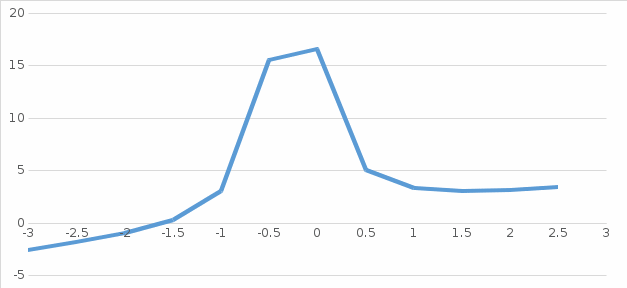
З а д а н и е 5
Вычислить с помощью дифференциала приближенное значение f (0) функции y = f (x) в точке a.
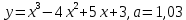
Решение:__З_а_д_а_н_и_е_9'>Решение:
Формула для приближенного вычисления с помощью дифференциала:
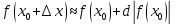
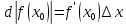
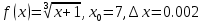
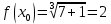
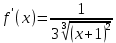
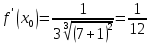
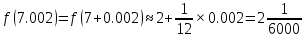
З а д а н и е 6
Найти наибольшее и наименьшее значение функции y = f (x) на промежутке [a; b].
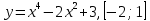
Решение:
Найдем критические точки.
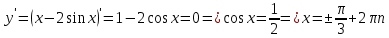
Вычисляем значения функции на концах отрезка и в критических точках:
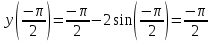
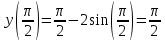
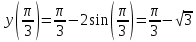
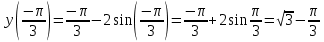
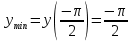
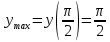
З а д а н и е 7
Решите задачу на отыскание наибольшего и (или) наименьшего значения.
Периметр осевого сечения цилиндра равен 6a. Найти наибольший объем цилиндра
Решение:
З а д а н и е 8
Взять неопределенные интегралы, используя таблицу интегралов, свойства линейности и основные методы: замены переменных и интегрирования по частям.
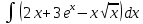
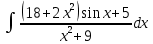
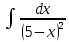
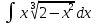
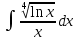
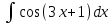
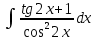
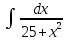
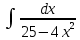
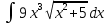
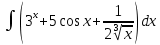
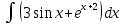
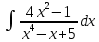
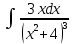
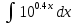
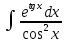
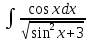
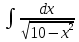
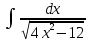
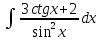
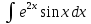
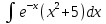
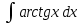
Решение:
З а д а н и е 9
Вычислить определённые интегралы, используя формулу Ньютона – Лейбница, свойства линейности и аддитивности, а так же основные методы: замены переменных и интегрирования по частям.
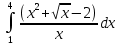
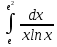
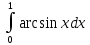
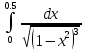
Решение:
З а д а н и е 10
Вычислить площадь фигуры, ограниченной линиями.
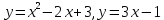
Одной аркой циклоиды
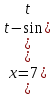
Двухлепестковой розой
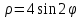
Решение:
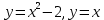
Найдем точки пересечения графиков функций
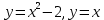
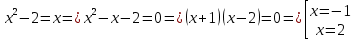
Изобразим графически фигуру, площадь которой предлагается найти:
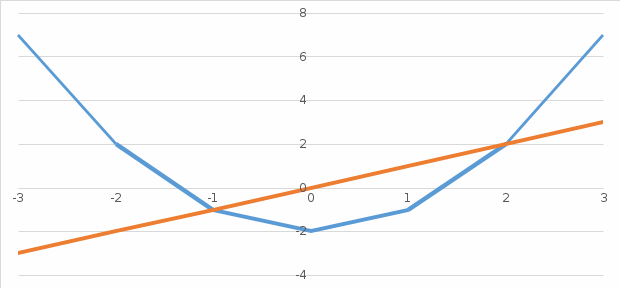
Если на отрезке [a,b] некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь фигуры, ограниченной графиками данных функций и прямыми x=a, x=b, можно найти по формуле:
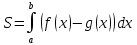
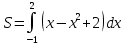
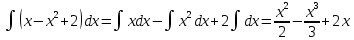
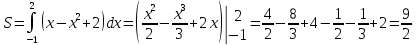
Эллипсом
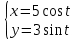
Площадь фигуры, заданной параметрически:
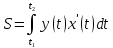
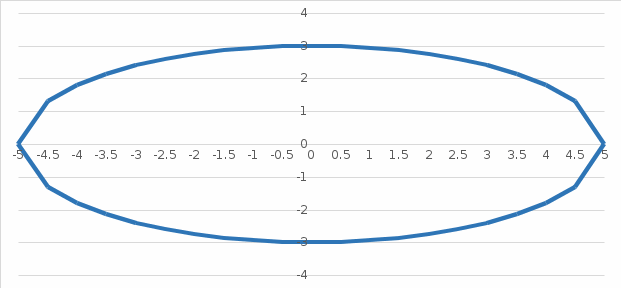
Так как фигура симметрична относительно оси абсцисс, поэтому вычислим верхнюю половину площади и удвоим результат.
Найдем значения параметра, которые определяют точки пересечения прямой эллипса с осью абсцисс:
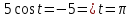
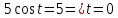
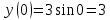
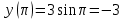
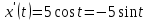
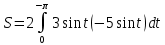
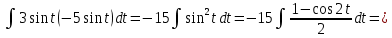
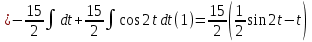
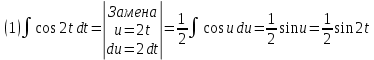
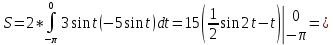
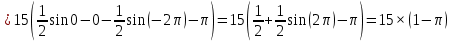
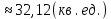
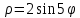
Заданное уравнение в полярной системе координат описывает окружность. Для наглядности построим график:
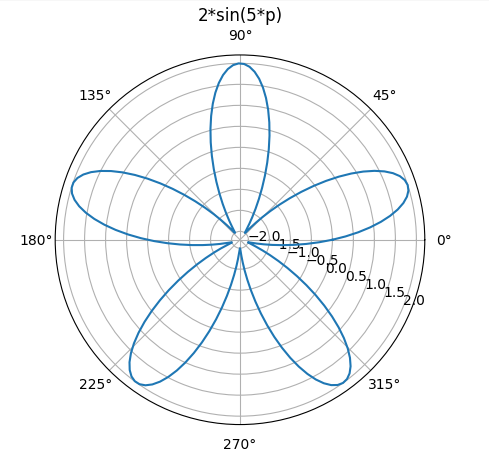
Находим два луча, между которыми лежит один из пяти лепестков розы, решая уравнение:
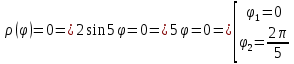
Площадь фигуры, заданной в полярной системе координат, вычисляется по формуле:
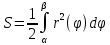 . Поскольку фигура состоит из 5 «лепестков», найдем площадь одного и умножим на 5.
. Поскольку фигура состоит из 5 «лепестков», найдем площадь одного и умножим на 5.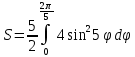
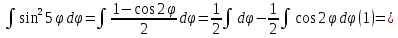
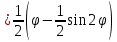
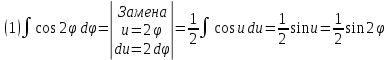
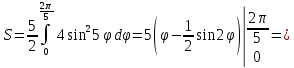
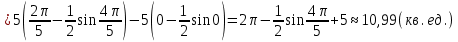
З а д а н и е 11
Найти длину дуги.
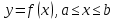
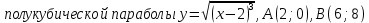
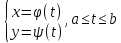
Астроиды
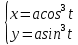
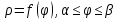
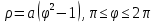
Решение:
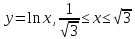
Длина кривой, график которой задан непрерывной функцией y= f(x) рассчитывается по следующей формуле:
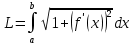
В данном случае
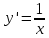
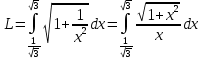
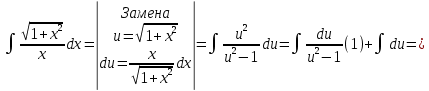
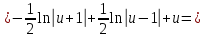
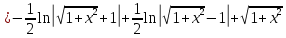
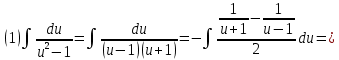
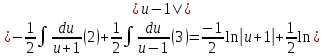
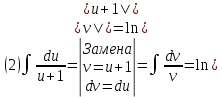
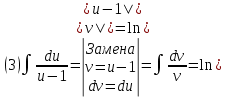
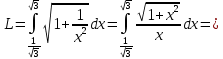
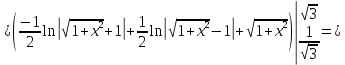
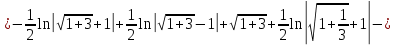
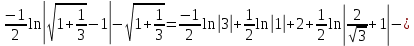
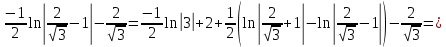
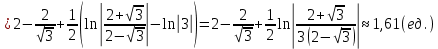
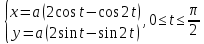
Если линия задана параметрическими уравнениями x=x(t), y=y(t), то длина дуги кривой, которая прочерчивается при изменении параметра t в пределах [t1,t2] , рассчитывается по формуле:
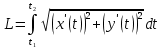
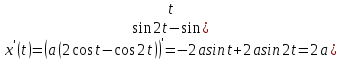
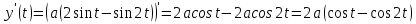
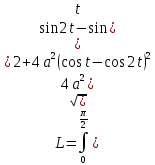
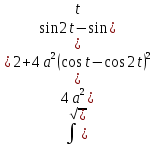
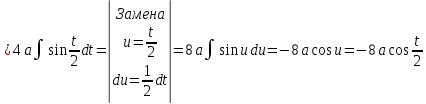
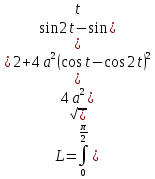
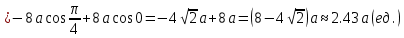
Спираль Архимеда
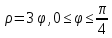
Если кривая задана в полярных координатах уравнением =(), где , при этом на промежутке [;] функция имеет непрерывную производную ’(), то длина дуги кривой выражается следующей формулой:
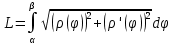
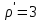
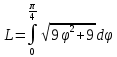
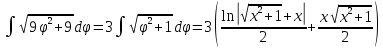
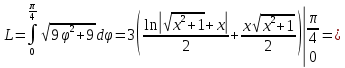
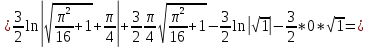
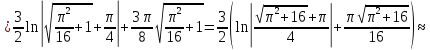
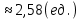
З а д а н и е 12
Найти объём тела, полученного вращением фигуры, ограниченной линиями.
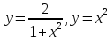 вокруг оси OY.
вокруг оси OY.Решение:
Изобразим схематически график функции y=f(x). Фигура, которая вращается вокруг оси ОХ, изображена на рисунке синим цветом.
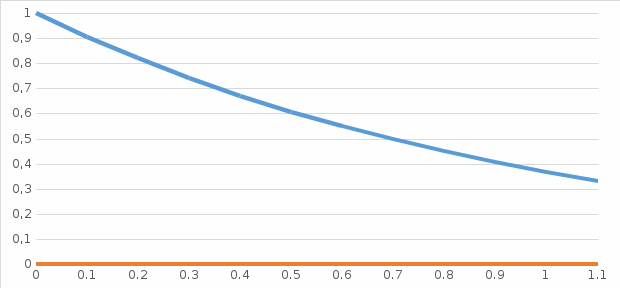
Объем тела вращения можно вычислить по формуле:
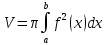
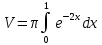
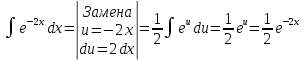
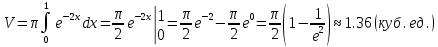
З а д а н и е 13
Найти область определения функции
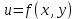 .
.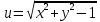
Решение:
З а д а н и е 14
Для функции z = f (x, y) найти частные производные до второго порядка включительно. Проверить равенство
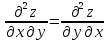 .
.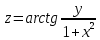
Решение:
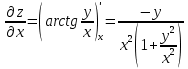
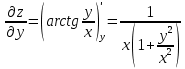
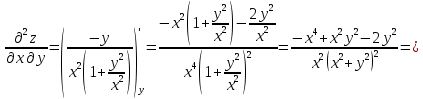
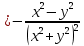
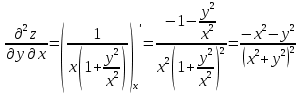
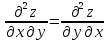
З а д а н и е 15
В мешке смешаны нити, среди которых 80% белые, а остальные – красные. Определить вероятность того, что вынутые на удачу 2 нити окажутся одного цвета.
Решение:
A - {сработало первое устройство}; P(A) = 0.7,
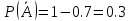
В – {сработало второе устройство}; P(B) = 0.9,
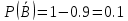
C – {сработало только одно устройство из двух}
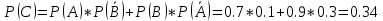
З а д а н и е 16
Решите задачу, используя формулу полной вероятности и формулу Байеса – Лапласа.
Сборщик получил 14 коробок деталей, изготовленных заводом №1 и 16 коробок деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна, равна 0,75, а заводом №2 – 0,8. Сборщик наудачу извлек деталь из наудачу взятой коробки. Извлечена нестандартная деталь. Определить вероятность того, что она изготовлена заводом №1.
Решение:
A - {студент попал в сборную};
В1 – {студент из 1 группы};
В2 – {студент из 2 группы};
В3 – {студент из 3 группы}.
Всего участвовали в соревнованиях 15 студентов.
P(B1) = 4/15
P(B2) = 6/15
P(B3) = 5/15
P(A/B1) = 0.6
P(A/B2) = 0.8
P(A/B3) = 0.5
По формуле полной вероятности:
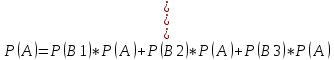
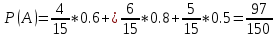
По формуле Байеса:
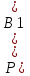
Вероятность того, что выбранный студент, попавший в сборную, из первой группы 24/97 (0,25)
З а д а н и е 17
Закон распределения дискретной случайной величины X задан в виде таблицы. Найти: математическое ожидание M(X); дисперсию D(X). Построить многоугольник распределения.
| X | 25 | 35 | 55 | 75 | 80 |
| P | 0,3 | 0,1 | 0,2 | 0,1 | 0,3 |
Решение:
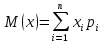
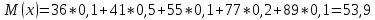
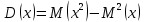
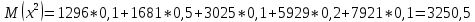
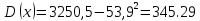
Многоугольник распределения:

З а д а н и е 18
Дано комплексное число z0. Требуется:
1) записать число z0 в алгебраической и тригонометрической формах;
2) изобразить его на комплексной плоскости;
3) найти все корни уравнения z3 − z0 = 0.
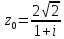
Решение:
Действительная часть x = 1
Мнимая часть
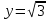
алгебраическая форма:
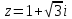
тригонометрическая форма:
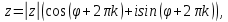
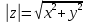
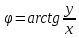
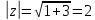
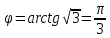
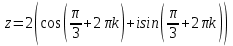
изобразить его на комплексной плоскости;
3) найти все корни уравнения z3 − z0 = 0.
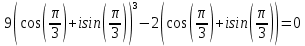
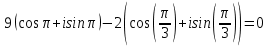
З а д а н и е 19
Решить систему уравнений SU тремя способами:
а) по формулам Крамера,
б) средствами матричного исчисления,
в) методом Гаусса.
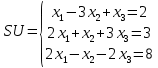
Решение:
а) метод Крамера
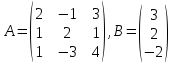
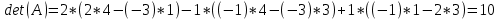
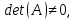 система имеет решение.
система имеет решение.Заменим 1-й столбец матрицы А на вектор В.
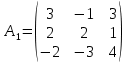
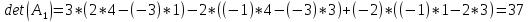
Заменим 2-й столбец матрицы А на вектор В.
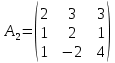
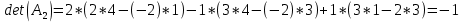
Заменим 3-й столбец матрицы А на вектор В.
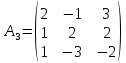
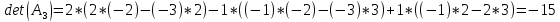
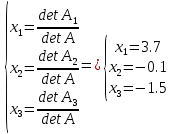
б) метод обратной матрицы:
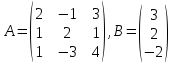
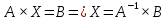
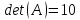
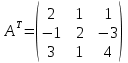
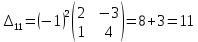
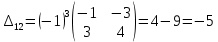
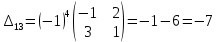
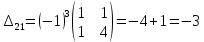
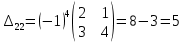
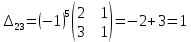
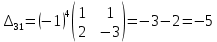
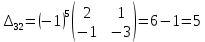
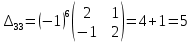
Из полученных алгебраических дополнений составим присоединенную матрицу C:
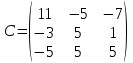
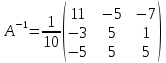
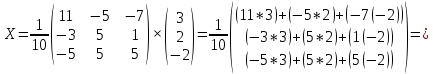
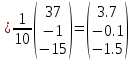
в) метод Гаусса
Расширенная матрица:
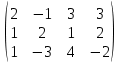
Умножим 2 строку на -1 и добавим к 3:
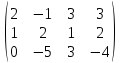
Умножим 1 строку на -1/2 и добавим к 2:
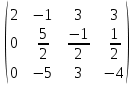
Поменяем местами 2 и 3 строки:
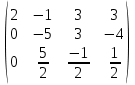
Умножим 2 строку на 1/2 и добавим к 3:
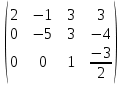
Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали:
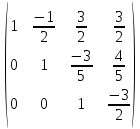
Исходную систему можно записать так:
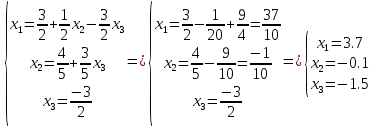
З а д а н и е 20
Найти решение дифференциального уравнения.
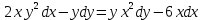
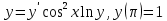
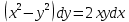
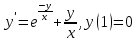
Решение:

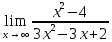
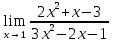
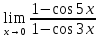
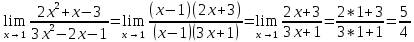
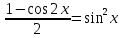
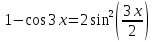
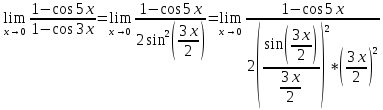
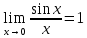
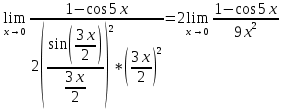
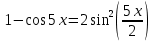
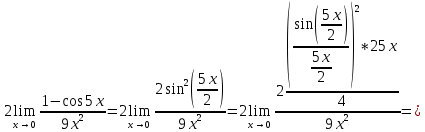
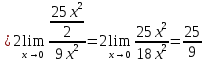
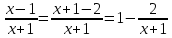
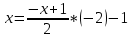
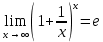
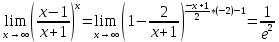
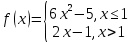
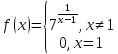
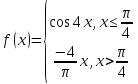
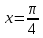
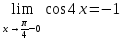
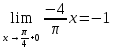
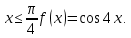 Так как косинус – периодическая функция, на отрезке
Так как косинус – периодическая функция, на отрезке 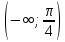 функция определена и непрерывна.
функция определена и непрерывна.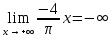
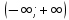
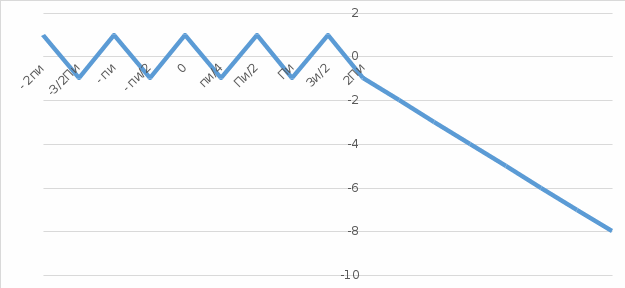
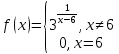
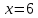
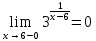
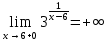
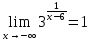
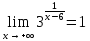
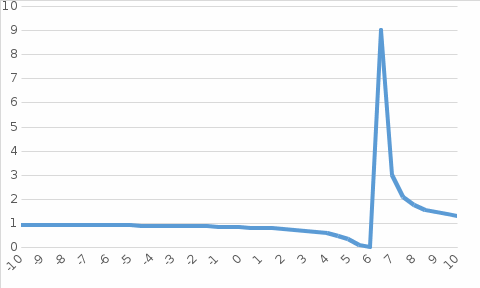
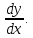
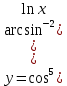
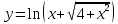
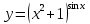
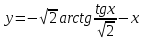
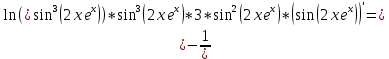
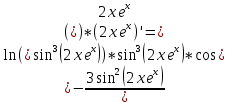
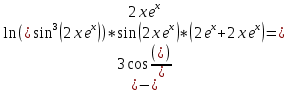
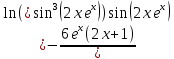
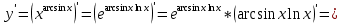
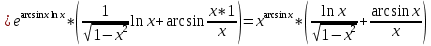
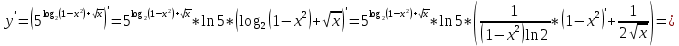
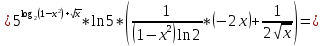
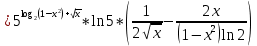
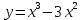
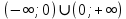
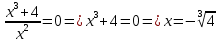
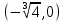
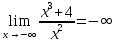
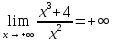
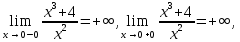 разрыв 2 рода.
разрыв 2 рода.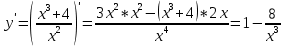
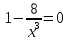
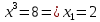
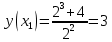
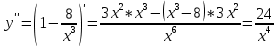
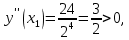 следовательно, точка минимума: (
следовательно, точка минимума: (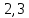 ).
).