Электрические измерения). Контрольная работа по дисциплине Электрические измерения
 Скачать 37.79 Kb. Скачать 37.79 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Интернет-институт ТулГУ
КОНТРОЛЬНАЯ РАБОТА по дисциплине Электрические измерения
Тула 2022 Задача 1. Измерены два значения напряжения U1 и U2 вольтметром с номинальным значением Amax с одной и той же абсолютной погрешностью 1 В. Требуется определить погрешность измерения какого из указанных значений напряжения меньше. Выполнить расчет значений погрешностей в соответствии с номером варианта, при условии, что шкала прибора Аmax = 1250 В. Заполнить пропущенные ячейки таблицы в соответствии с полученными результатами. Исходные данные: U1 = 250 B; U2 = 1000 B. Решение: Вид шкалы в условии задачи не указан, следовательно, используется прибор с односторонней шкалой, у которого Amin = 0, Аmax = 1250 В, поэтому uном = 1250 В. Класс точности прибора не указан в условии задачи. Принимаем класс точности вольтметра, равный К.т. = 1. Тогда определим значение абсолютной погрешности, используя формулу приведенной погрешности. Наибольшее значение приведенной погрешности в рабочем диапазоне шкалы измерительного прибора называют основной приведенной погрешностью, выражают в процентах и указывают на шкале этого прибора: γ = 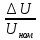 · 100%, · 100%,где ΔU – абсолютная погрешность, В; UN – предел измерения шкалы прибора, В. ΔU = 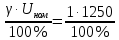 = 12,5 В. = 12,5 В.Относительная погрешность равна отношению абсолютной погрешности к действительному значению измеряемой величины и выражается в процентах: δ = 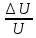 · 100% · 100%γд1 = 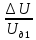 · 100% = · 100% = 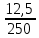 · 100% = 5 %; · 100% = 5 %;γд2 = 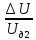 · 100% = · 100% = 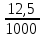 · 100% = 1,25 %. · 100% = 1,25 %.Результаты расчетов заносим в таблицу:
Таким образом, при измерении напряжения 250 В относительная погрешность составила 5 %, а при измерении напряжения 1000 В составила 1,25 %. Погрешность при этом уменьшилась в 4 раза. Задача 2 Выполнить расчет значения относительной приведенной погрешности. Заполнить пропущенные ячейки таблицы в соответствии с полученными результатами и в соответствии с вариантом задания. Исходные данные:
Определить: γпр, К.Т. Решение: Максимальная абсолютная погрешность измерения Δmax = 301 - 300 = = 1 В, номинальное напряжение Uном= 375 - 0 = 375 В, тогда γпр = 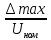 · 100%, · 100%,γпр = 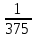 · 100% = 0,27 %. · 100% = 0,27 %.Полученное значение попадает в существующие классы точности прибора, поэтому присваиваем данному вольтметру класс точности – 0,5 %. Следует отметить, что класс точности прибора, определяя приведенную погрешность, не является непосредственным показателем точности измерений.
Задача 3 Для измерения тока 4 мА имеются два миллиамперметра: первый - класса точности 1 % с верхним пределом 20 мА и второй - класса точности 2,5 % с верхним пределом 5 мА. Требуется определить, каким прибором заданный ток можно измерить с меньшими абсолютной и относительной погрешностями. Выполнить расчет значений погрешностей. Выбрать миллиамперметр, который обеспечит большую точность измерений. Заполнить пропущенные ячейки таблицы в соответствии с полученными результатами и согласно варианту задания. Решение: Относительные действительные погрешности измерения определяем по формуле (2.4): γд1 = γпр1 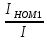 = 1% = 1% 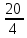 = 5 %; = 5 %;γд2 = γпр2 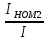 = 2,5% = 2,5% 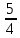 = 3,125 %. = 3,125 %.Следовательно, стрелка второго миллиамперметра (более низкого класса точности) при измерении будет находиться в четвертой четверти шкалы, а стрелка первого миллиамперметра, имеющего класс точности 1 %, - в первой. Абсолютные погрешности измерения определяем по формуле (2.2): ∆1 = 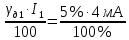 = 0,2 мА; = 0,2 мА;∆1 = 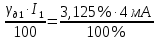 = 0,125 мА. = 0,125 мА.
Таким образом, более точные измерения можно выполнить при помощи второго амперметра. Задача 4 Выбрать оптимальный предел измерения вольтметра и оценить погрешность этого измерения. Заполнить пропущенные ячейки таблицы в соответствии с полученными результатами. (Значение оптимального предела записать в вольтах). Решение: Примем класс точности указанного вольтметра, равный, 0,5 %. Оптимальным положение стрелки вольтметра для данного измерения, а, следовательно, для обеспечения меньшей погрешности является в пределах 30 В и 60 В.. Тогда определяем γд = γпр 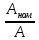 ; ;γд3 = 0,5 % 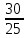 = 0,6 %; = 0,6 %;γд4 = 0,5 % 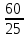 = 1,2 %. = 1,2 %.Расчеты показывают, что измерение напряжения на пределе 30 В действительно является оптимально верным вариантом с наименьшей погрешностью 0,6 %.
Задача 5 Определить относительную и абсолютную погрешности установки. Заполнить пропущенные ячейки таблицы в соответствии с полученными результатами. Решение: Относительная погрешность: γдF = ± (2 + 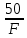 ); );γдF = ± (2 + 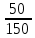 ) = ± 2,33 %. ) = ± 2,33 %.Абсолютную погрешность установки частоты 120 Гц определяем из формулы: ∆1 = 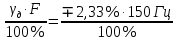 = 3,49 Гц. = 3,49 Гц.
Задание 6 Определить относительную и абсолютную погрешности установки. Заполнить пропущенные ячейки таблицы в соответствии с полученными результатами. Решение: 1.Абсолютная погрешность установки частоты: ∆F = ± (2 + 0,07 · 280) = ± 21,6 Гц. 2.Относительную погрешность установки частоты определяем по формуле: γдF = 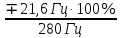 = ± 7,71 %. = ± 7,71 %.В практике электрорадиоизмерений прибор часто не соответствует установленному заводом-изготовителем классу точности из-за его естественного износа (старения) или вследствие неправильной эксплуатации. В этом случае возможны два варианта действий: замена такого прибора исправным или использование его с учетом графика поправок.
Задача 7 Определить относительную и абсолютную погрешности установки. Рассчитать и построить график поправок для измерений. Заполнить пропущенные ячейки таблицы в соответствии с полученными результатами. Исходные данные:
Абсолютная погрешность измерения составила:
Решение: Найдем относительную приведенную погрешность по формуле: γпр = 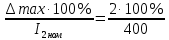 = 0,5 % = 0,5 %Следовательно, класс точности прибора не сохранился (не соответствует заводскому). Для обеспечения возможности дальнейшего использования прибора из формулы (2.3) определим его максимальную допустимую абсолютную погрешность при заводском классе точности 0,2 %: ∆max = 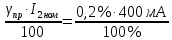 = 0,8 мА. = 0,8 мА.Так как абсолютная погрешность не постоянна, поправка рассчитывается следующим образом: с = 0, если Δ ≤ Δmax; с = Δ - Δmax если Δ > Δmax. Для рассматриваемого прибора поправки по оцифрованным делениям шкалы составят соответственно: 0; 0; 0,45; 0,2; 0,7; 1,2, график поправок будет иметь вид: 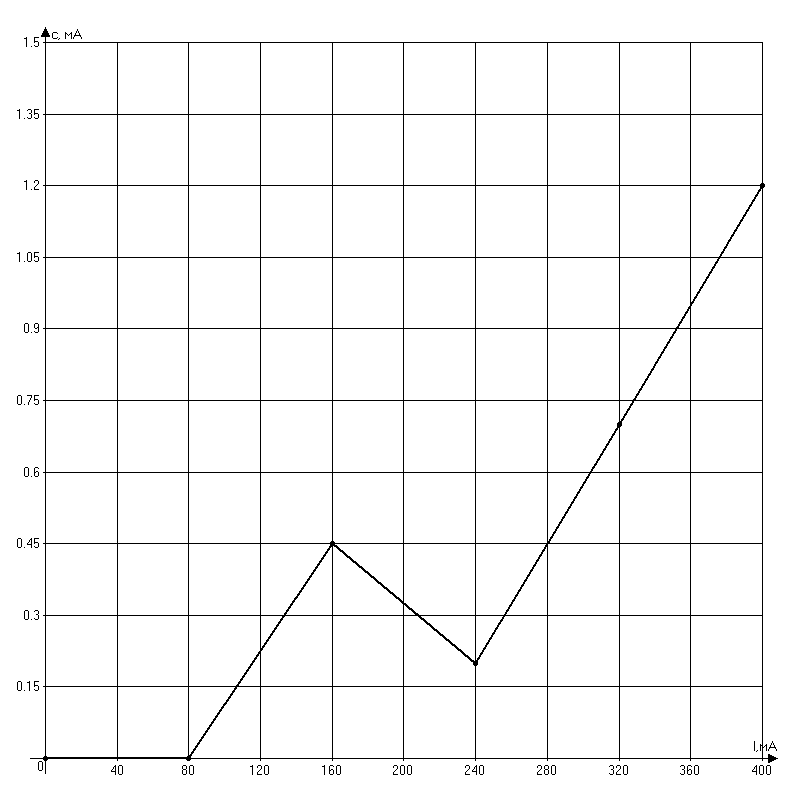 Проверим правильность полученного графика поправок. Предположим, что миллиамперметром был измерен ток 320 мА. С учетом поправки I = 320 + 0,7 = 320,7 мА. Абсолютная погрешность ∆ = Iи – I = 321,5 – 320,7 = 0,8 мА, что не превышает рассчитанную ∆max. Относительная приведенная погрешность: γпр = 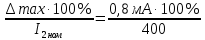 = 0,2 % = 0,2 %
Задача 8 Определить сопротивление резистора, а также относительную и абсолютную погрешности измерительного устройства. Заполнить пропущенные ячейки таблицы в соответствии с полученными результатами. Решение: Для определения сопротивления резистора используем закон Ома: R = 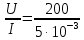 = 40 кОм. = 40 кОм.Формулу для расчета R перепишем в виде R = U1I-1, откуда можно записать, что k1 = 1, k2 = -1. В формулу для определения погрешности косвенных измерений (2.5) вместо γд1 подставим γдU, так как k1 относится к напряжению, а вместо γд1 подставим γдI, так как k2 относится к току, т.е. запишем: γdR = 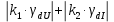 . .Напряжение и ток измерялись прямым методом, следовательно: γdU = γпр 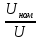 = 1,5 · = 1,5 · 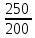 = 1,875 % = 1,875 %γdI = 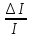 · 100% = · 100% = 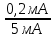 ·100 % = 4 %. ·100 % = 4 %.Тогда γdR = 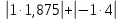 = 5,875 % = 5,875 %Абсолютную погрешность сопротивления резистора найдем по формуле: ∆R = 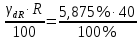 = 2,35 кОм. = 2,35 кОм.
|
