эдирр. ЭДиРР. Контрольная работа по дисциплине электродинамика и распространение радиоволн Выполнил студент 3 курса специальности 25. 05. 03
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА ИРКУТСКИЙ ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА) КАФЕДРА АРЭО КОНТРОЛЬНАЯ РАБОТА По дисциплине: электродинамика и распространение радиоволн Выполнил студент 3 курса специальности 25.05.03 шифр: 1851475 Проверил преподаватель Иркутск 2021 ОглавлениеЗадача 1. Плоские электромагнитные волны 3 Задача 2. Линии передачи высокочастотного диапазона 8 Задача 3. Объемные резонаторы 17 Задача 1. Плоские электромагнитные волныЗадано Плоская однородная волна частоты Требуется определить: 1. Нормальные 2. У падающей волны: коэффициент фазы, фазовую и групповую скорости и длину волны вдоль направления падения волны: 3. Модуль усредненного по времени вектора Умова-Пойнтинга падающей волны. 4. Эффективную поверхностную плотность тока 5. Удельное поверхностное сопротивление 6. Полное сопротивление проводника с размерами 7. Удельную 8. Написать, при какой поляризации может иметь место явление полного преломления (т.е. отсутствует отраженная волна) и при каких условиях может наступить явление полного отражения (т.е. отсутствует преломленная волна) и определить угол Брюстера и критический угол падения, если  Рис. 1. Отражение и преломление плоской однородной волны на плоской границе раздела двух сред при горизонтальной поляризации  Рис. 2. Фазовая, групповая скорости и длина волны Решение 1. Определим нормальные и касательные к границе компоненты полей падающей волны:  , ,где 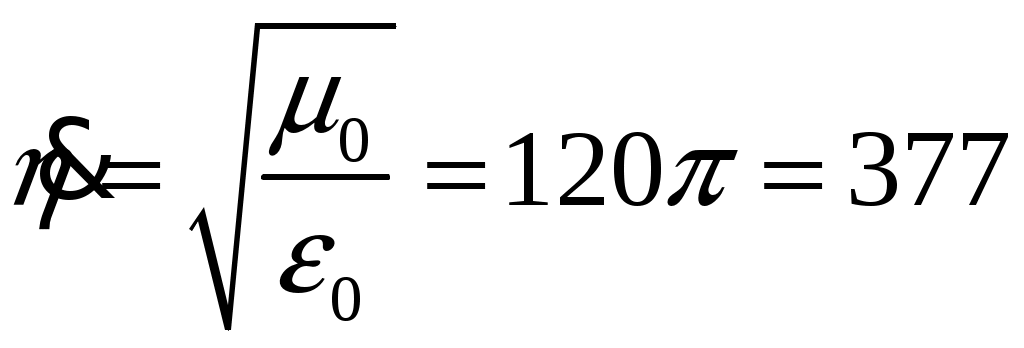 Ом, Ом, А/м, А/м,2. Циклическая частота Коэффициент фазы вдоль направления падения волны Фазовая скорость вдоль направления падения волны 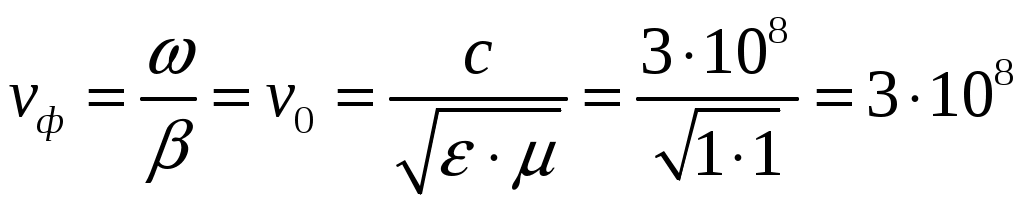 м/с. м/с.Групповая скорость вдоль направления падения волны 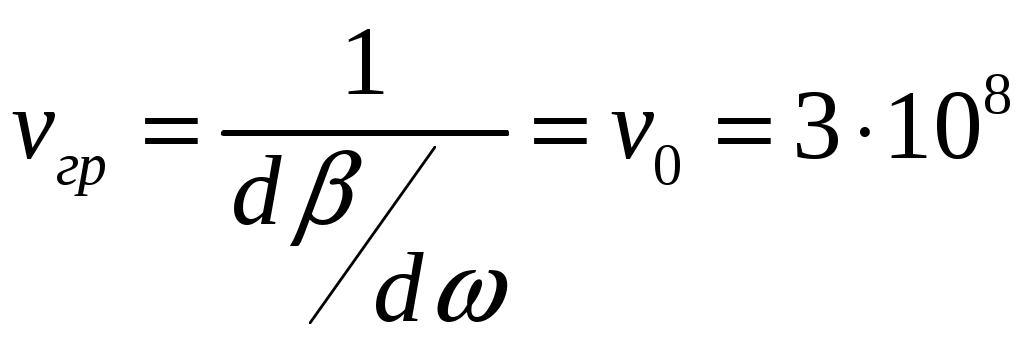 м/с. м/с.Длина волны вдоль направления падения волны  м. м.Коэффициент фазы по направлению вдоль оси Фазовая скорость по направлению вдоль оси  м/с. м/с.Групповая скорость по направлению вдоль оси Длина волны по направлению вдоль оси 3. Модуль усредненного по времени вектора Умова-Пойнтинга падающей волны  Вт/м2. Вт/м2.4. Эффективная поверхностная плотность тока при горизонтальной поляризации 5. Удельное поверхностное сопротивление отражающей поверхности  Ом. Ом.Глубина проникновения 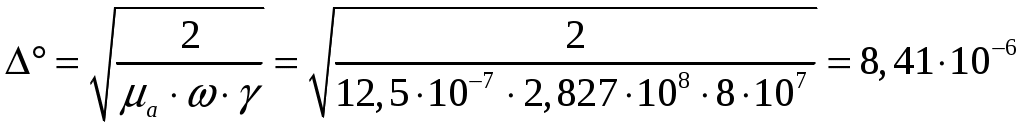 м. м.6. Полное сопротивление проводника  Ом. Ом.7. Удельная мощность тепловых потерь Полная мощность тепловых потерь на отражающей поверхности с площадью 8. При угле падения, равном углу Брюстера, имеет место полное преломление:  , , . .Явление полного отражения имеет место при угле падения, не меньшем критического  , , . .Задача 2. Линии передачи высокочастотного диапазонаЗадано При расчетах необходимо пользоваться только системой единиц СИ. Заданы: форма поперечного сечения волновода (прямоугольная) и тип волны в нем ( Требуется выполнить следующее: 1. Выбрать поперечные размеры прямоугольного волновода по заданным рабочим частотам. Стандарт на волноводы приведен в табл. 3. 2. Найти значения 3. Используя найденные в п. 2. значения 4. Найти поперечные размеры волновода при работе с высшими типами волн (при заданной рабочей волне 5. Найти критическую частоту и критическую длину волны заданного типа. 6. Найти длину волны в волноводе, фазовую и групповую скорости на средней длине волны. 7. Найти максимально допустимую длину волновода, при которой не наблюдалось бы заметных искажений формы сигнала при работе короткими импульсами высокой частоты 8. Рассчитать предельную мощность в волноводе на средней частоте при выбранных его стандартных размерах. Найти пробивную мощность при 9. Найти коэффициент затухания на средней частоте. 10. Найти отношение амплитуд поля (при 11. Определить, на каком расстоянии амплитуды поля волн 12. Найти КПД несогласованной с нагрузкой линии передачи при длине линии Решение 1. Предварительно найдем длины волн рабочего диапазона:  м/с, м/с, м, м, м. м.Условия для выбора размеров прямоугольного волновода для волны Выбираем волновод R40: 2. Для прямоугольного волновода  1/м, 1/м,Коэффициент фазы в волноводе где  рад/с, рад/с,3. Для прямоугольного волновода из решения уравнений Максвелла с выполнением граничных условий на идеально проводящих стенках получаются решения для комплексных амплитуд поля волн типа   , ,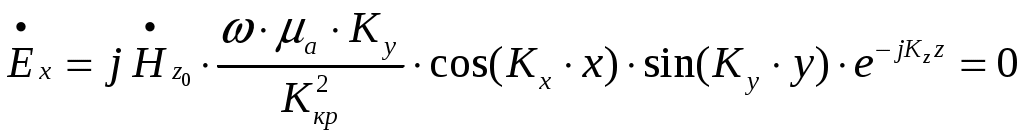 , ,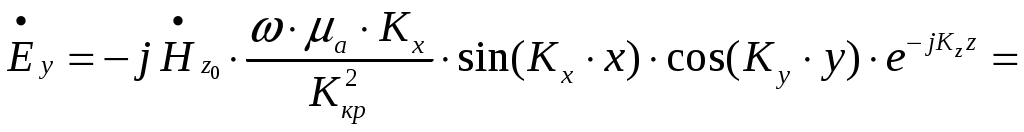 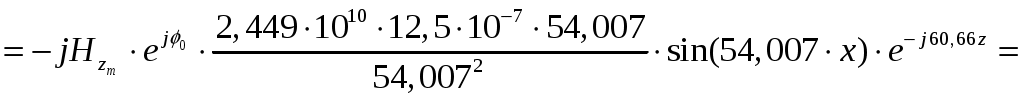 4. Критическая длина волны 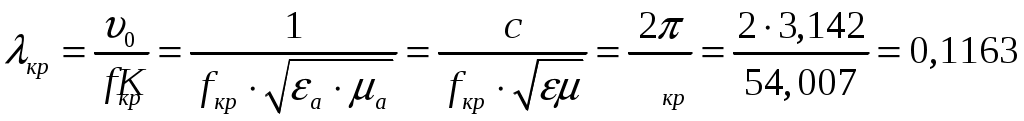 м, м, , ,Таким образом, поперечные размеры волновода получаются меньше при работе с основной волной. 5. В прямоугольном волноводе критические частоты волн типа   рад/с. рад/с.Критическая длина волны  м. м.6. Длина, соответствующая заданной длительности импульса, Длина волны в волноводе   м. м.Фазовая скорость   м/с. м/с.Групповая скорость   м/с. м/с.7. Максимально допустимая длина волновода, при которой искажения еще невелики,  , ,где  м. м.8. Предельная мощность в прямоугольном волноводе на средней частоте и волне типа   Пробивная мощность  Вт. Вт.Максимально допустимая мощность  Вт. Вт.Рабочая мощность  Вт. Вт.Условие выполняется: 9. Коэффициент затухания волн типа  , ,где  Ом, Ом, 10. Найдем отношение амплитуд поля и отношение мощностей можно найти из следующей формулы  , дБ/м, , дБ/м, , , . .11. Критическая длина волны типа  м. м.Коэффициент закритического затухания   дБ/м. дБ/м.Определим расстояние  , , м. м.12. Коэффициент полезного действия несогласованной с нагрузкой линии передачи  , ,где Модуль коэффициента отражения где 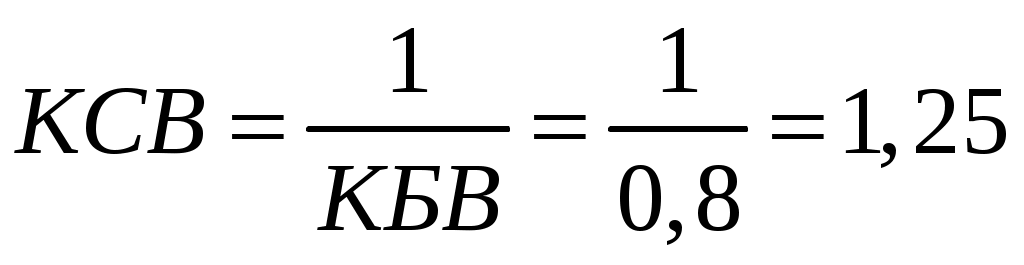 , , . .Коэффициент затухания  Неп/м, Неп/м,Задача 3. Объемные резонаторыЗадано Задана форма резонатора (параллелепипед) и тип колебания ( Требуется выполнить следующее: 1. Нарисовать картину поля заданного типа колебания, используя рис. 3. 2. Записать выражения для компонент поля соответствующего типа колебаний. В эти выражения надо подставить числовые значения 3. Найти резонансную частоту 4. Запасенную энергию электромагнитного поля 5. Глубину проникновения в материал стенок. 6. Добротность резонатора 7. Постоянную времени Решение 1. Картина поля заданного типа колебания: 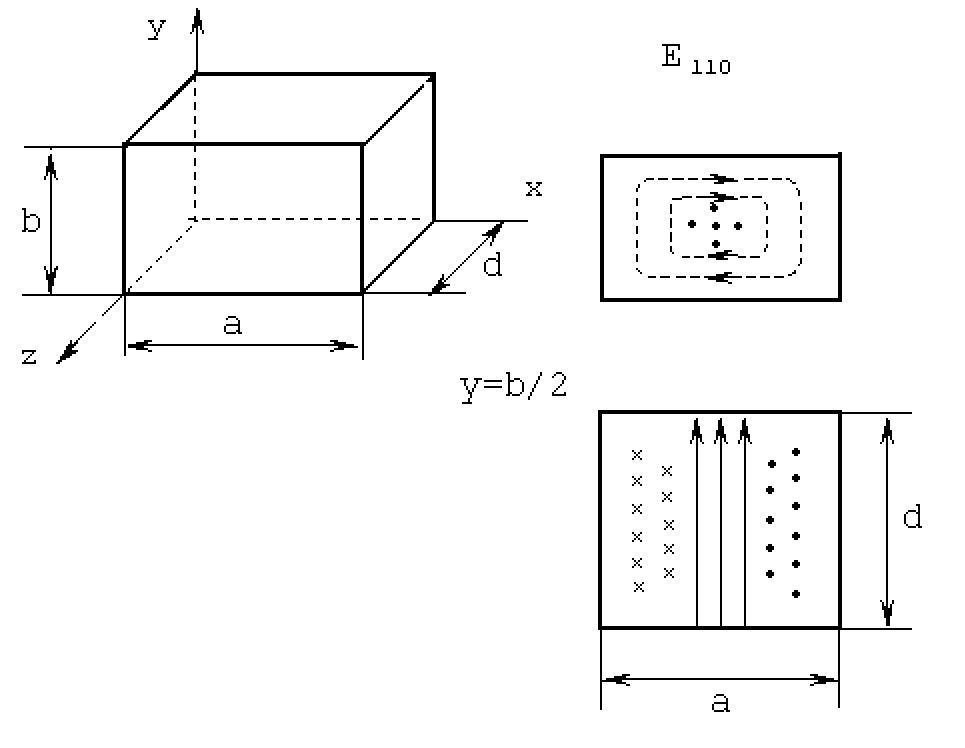 2. Числовые значения  1/м, 1/м, 1/м, 1/м,Для прямоугольного резонатора составляющие поля для колебаний типа  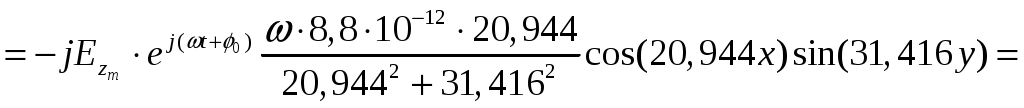  , ,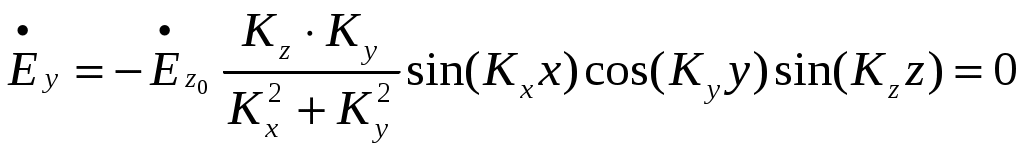 , ,3. Резонансная частота в прямоугольном резонаторе с колебаниями типа   рад/с. рад/с.4. Запасенная электромагнитная энергия 5. Глубина проникновения в материал стенок  м. м.6. Добротность резонатора без учета потерь в диэлектрике 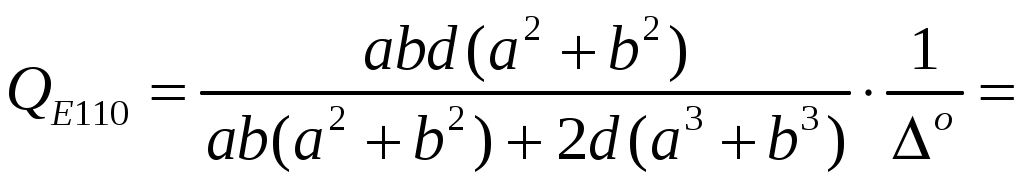 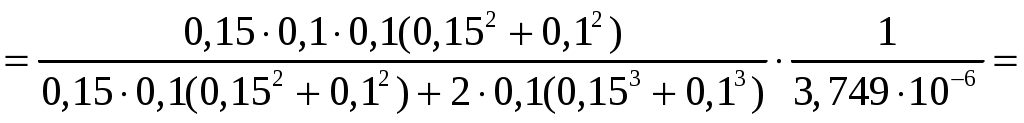 = 9544. 7. Постоянная времени  с. с.За время раз. Таким образом, энергия будет практически равна нулю. |
