«Электротехника и электроника». вариант 9. Контрольная работа по дисциплине Электротехника и электроника студент группы
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Контрольная работа по дисциплине «Электротехника и электроника» Выполнил: студент группы Проверил: Преподаватель: ________________ Нечаева Т.В. (подпись) Иркутск, 2021 ВАРИАНТ 9  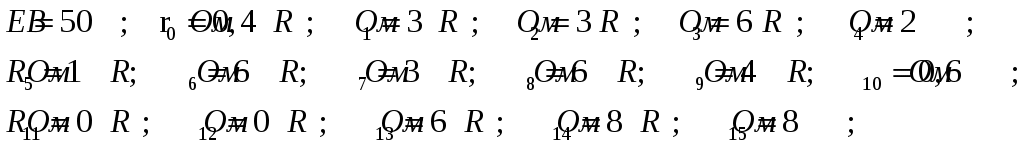 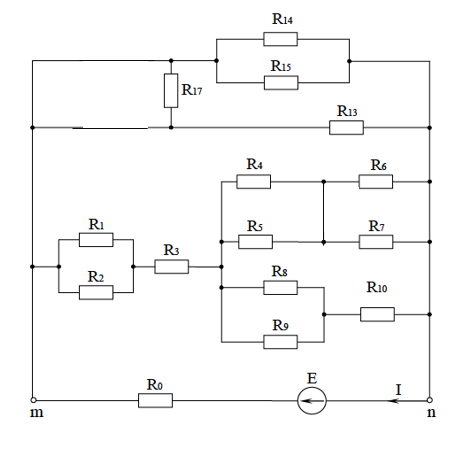 Рис.1 Расчетная схема согласно варианту. Решение: Производим свертывание схемы Сопротивления 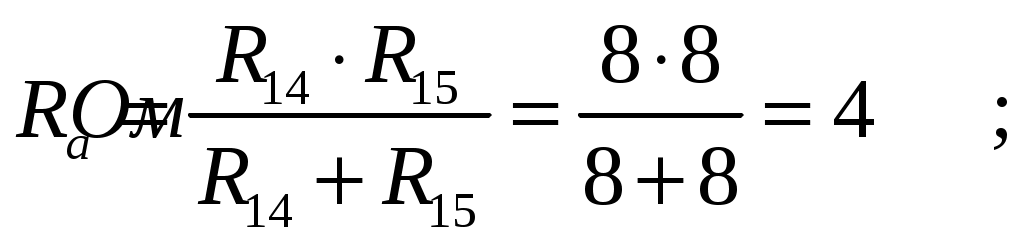 Сопротивления 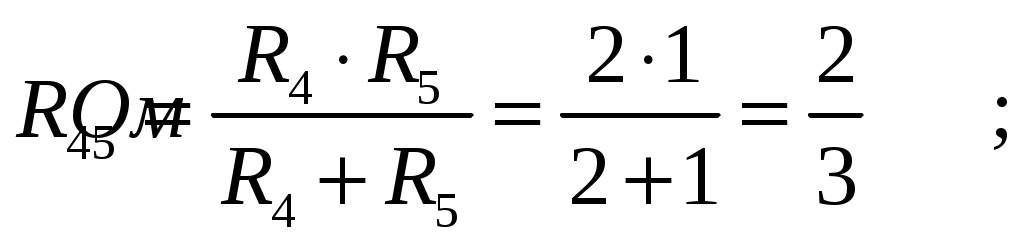 Сопротивления 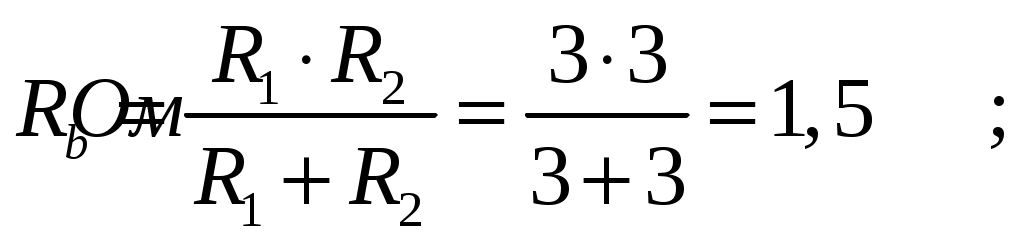 Сопротивления 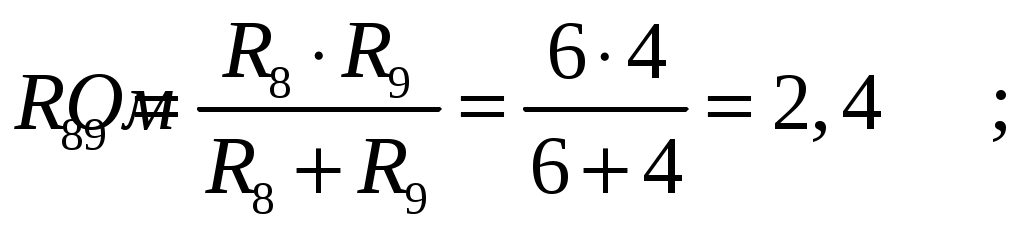 Сопротивления 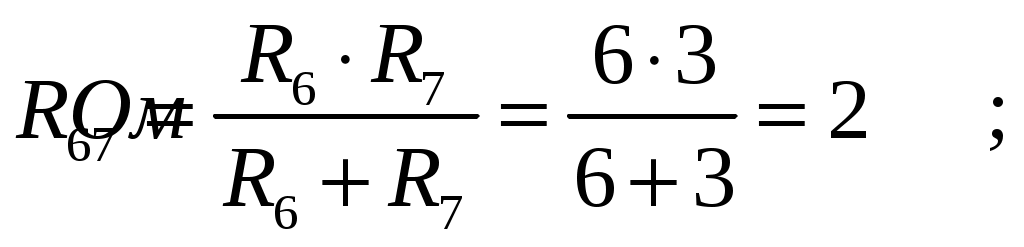 R17 – закорочено Перечерчиваем схему: 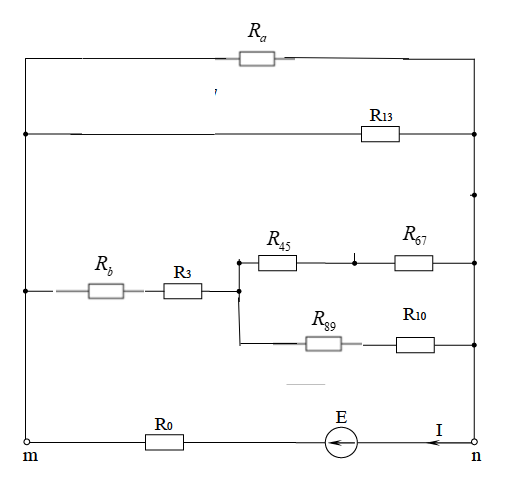 Рис.2 Сопротивления Сопротивления 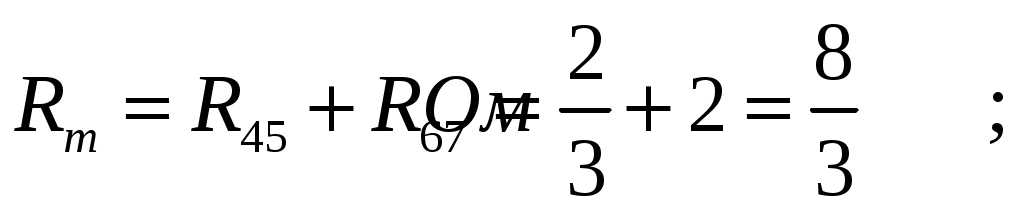 Сопротивления , 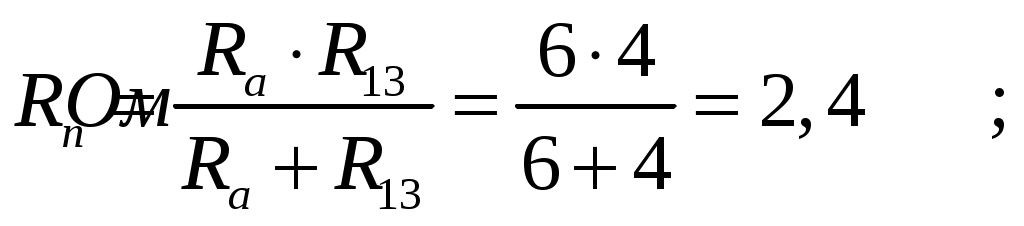 Сопротивления Перечерчиваем схему: 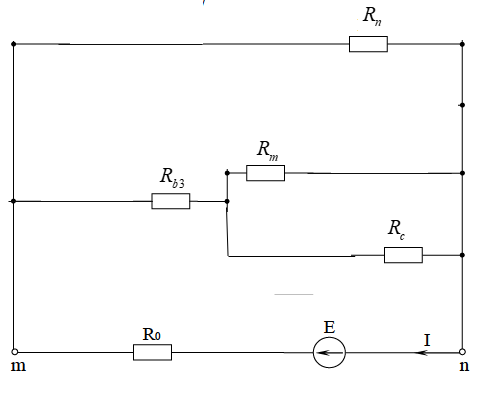 Рис.3. Сопротивления 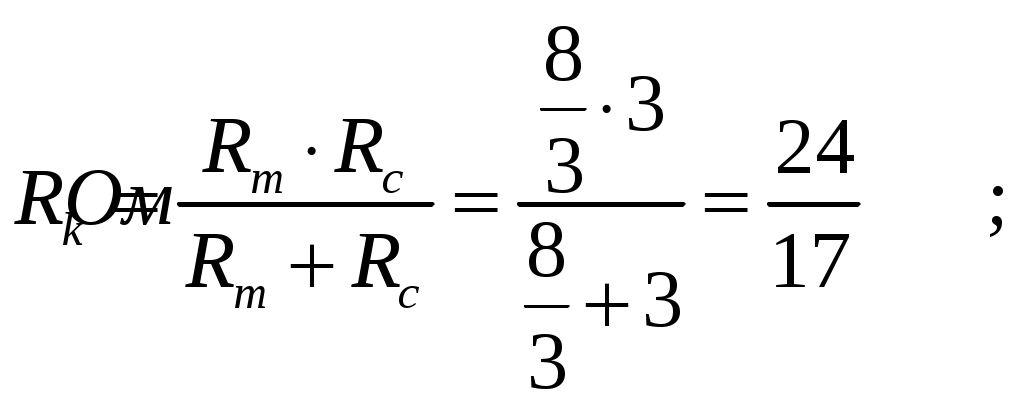 Перечерчиваем схему: 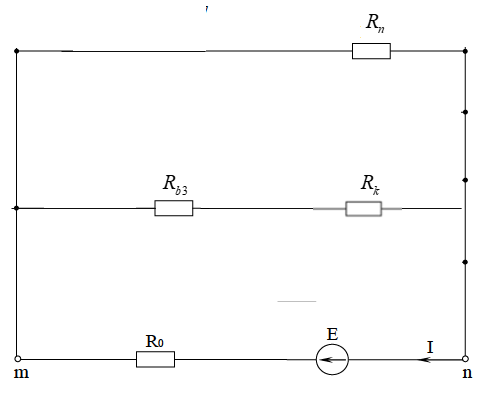 Рис.4. Сопротивления 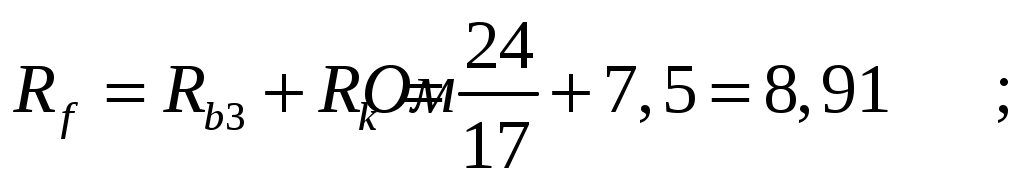 Перечерчиваем схему: 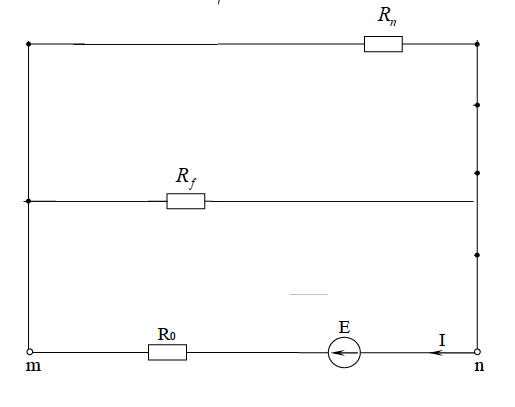 Рис.5 Сопротивления 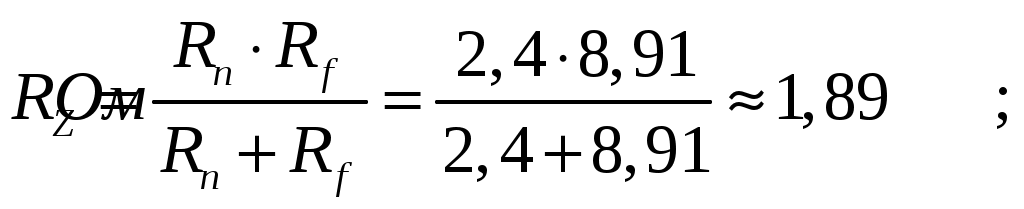 Перечерчиваем схему: 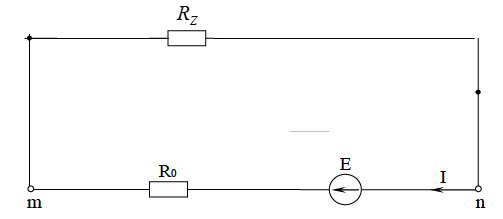 Рис.6. Видно, что два элемента соединены последовательно: Таким образом, входное сопротивление данной схемы : 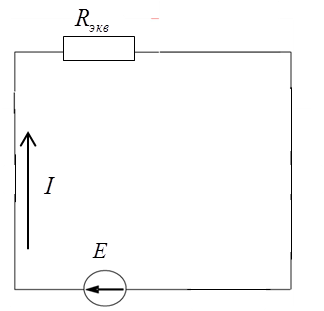 Рис.7. По закону Ома определяем общий ток: 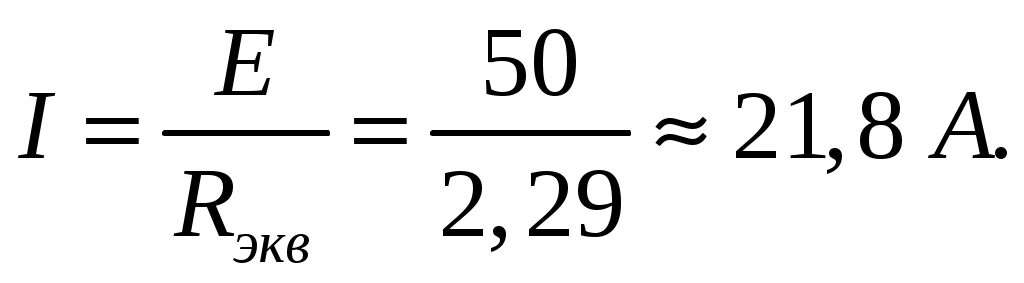 
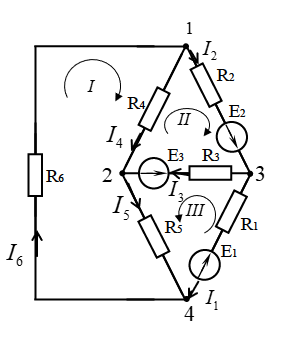 Рис.2.18. Расчетная схема Решение Выберем произвольно направление токов в ветвях и укажем их стрелками на схеме. В схеме 6 ветвей (в=6), 4 узла (у=4). Неизвестных токов в исходной схеме 6. По законам Кирхгофа необходимо составить 6 уравнений. По первому закону Кирхгофа: у-1=4-1=3независимых уравнений. По второму закону Кирхгофа в-(у-1)=6-(4-1)=3 уравнения для независимых контуров Узел 1: Узел 2: Узел 3: Контур І: Контур ІІ: Контур ІІІ: . Преобразуем схему цепи в эквивалентную посредством замены пассивного треугольника схемы эквивалентной звездой, рассчитав сопротивления её лучей (ветвей). Заменим пассивный треугольник сопротивлений 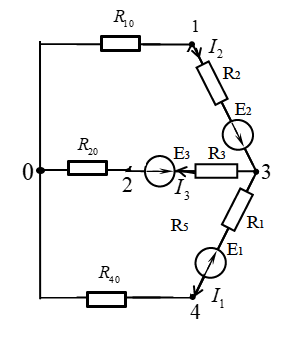 Рис.2.18.1 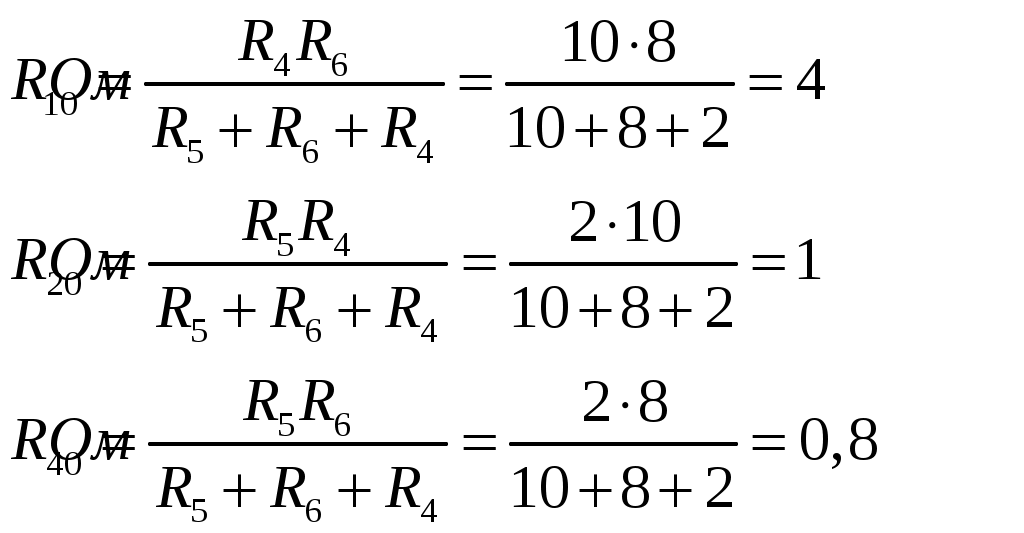 Рассчитаем упрощенную схему цепи методом узловых напряжений (методом двух узлов). 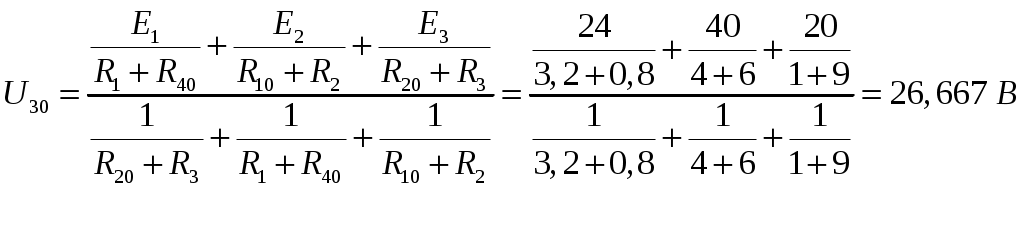 Токи в ветвях найдем по обобщенному закону Ома: 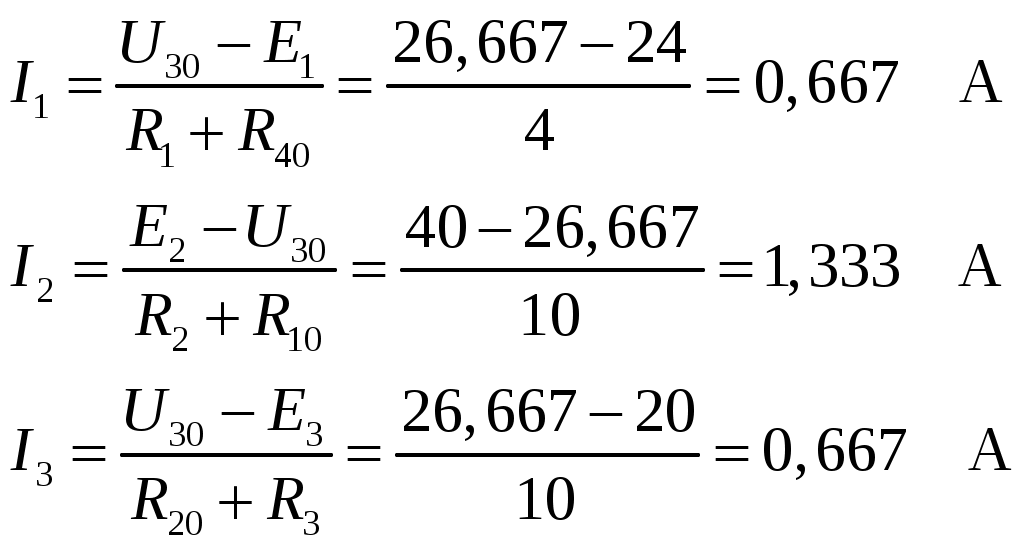 Сделаем проверку по 1 закону Кирхгофа: 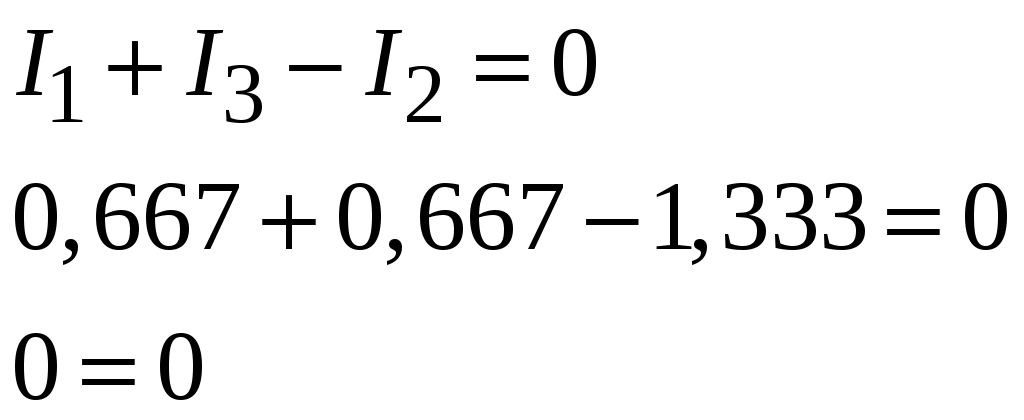 4) В исходной схеме ( рис.2.18) По 2 закону Кирхгофа: для контура ІІ: отсюда 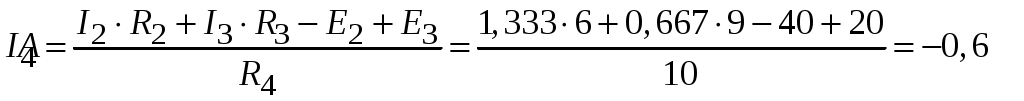 Для контура ІІІ: отсюда 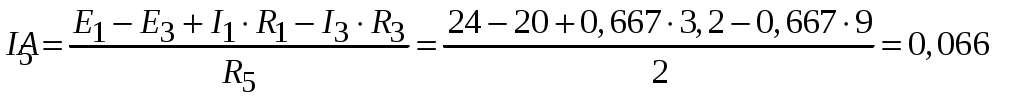 для контура І: отсюда 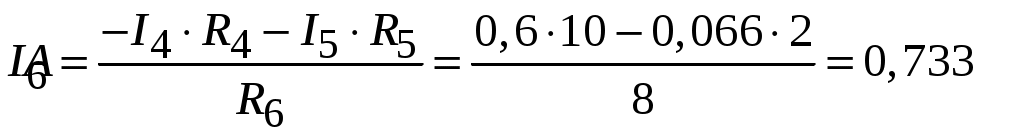 5) Составим баланс мощностей . Мощность источников равна: Мощность потребителей равна 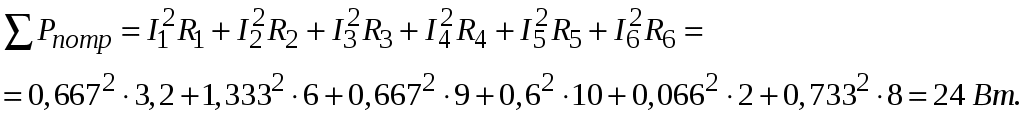  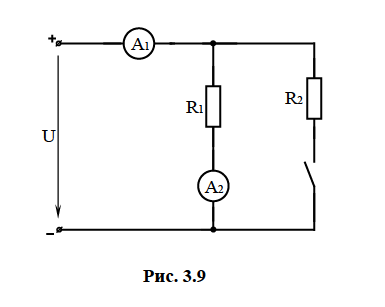 До замыкания рубильника, цепь имела только сопротивление R1 и показания амперметров были равны. После замыкания рубильника эквивалентное сопротивление двух паралелльно соединенных резисторов R1 и R2 ( оно же эквивалентное сопротивление цепи), уменьшится, а значит увеличится ток через ампеметр А1. Ток через А2 не изменится, так как не изменилось входное напряжение, к которому подсоединен R1   Решение Изобразим схему согласно варианта 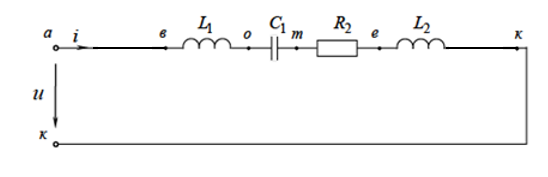 Найдем угловую частоту: Найдем сопротивления реактивных элементов: 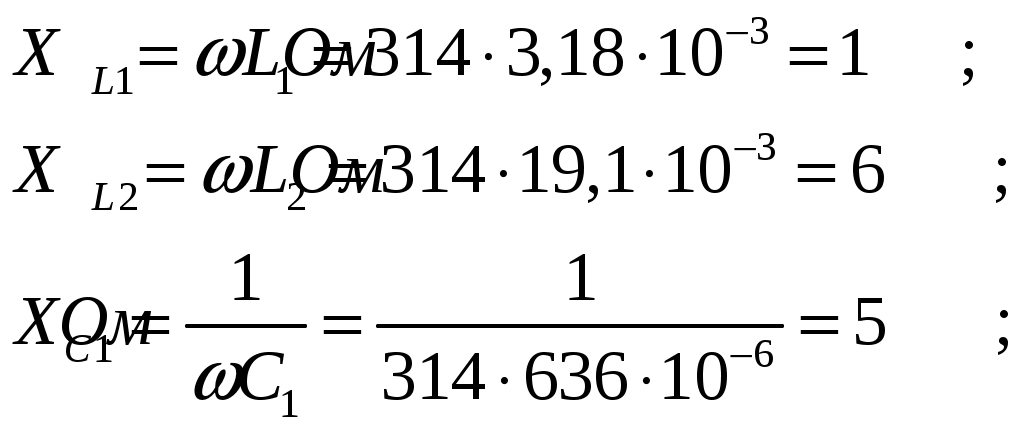 Полное сопротивление цепи: По закону Ома 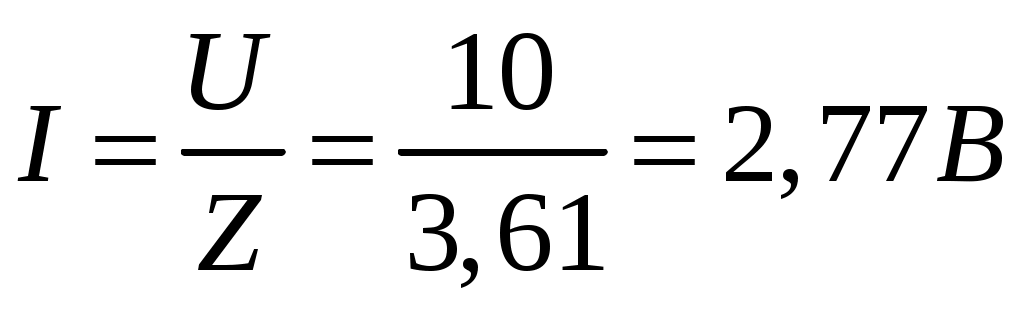 Мгновенное значение входного напряжения в общем виде Тогда Угол сдвига фаз между напряжением и током в цепи: 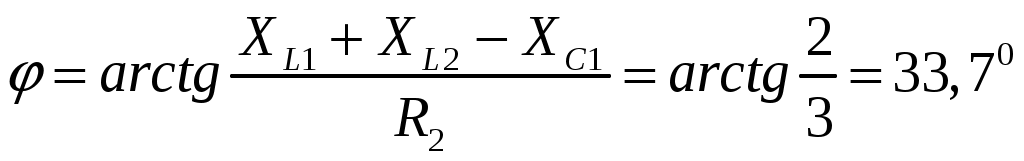 Мгновенное значение тока в общем виде В нашем случае: Полная, активная и реактивная мощности цепи : Для построения топографической векторной диаграммы необходимо сначала рассчитать комплексные напряжения на каждом элементе схемы, а затем начать построение диаграммы с общей величины – вектора тока I, после чего построить последовательно друг за другом вектора напряжений, начиная с В комплексной форме : Определение падения напряжений на элементах цепи. 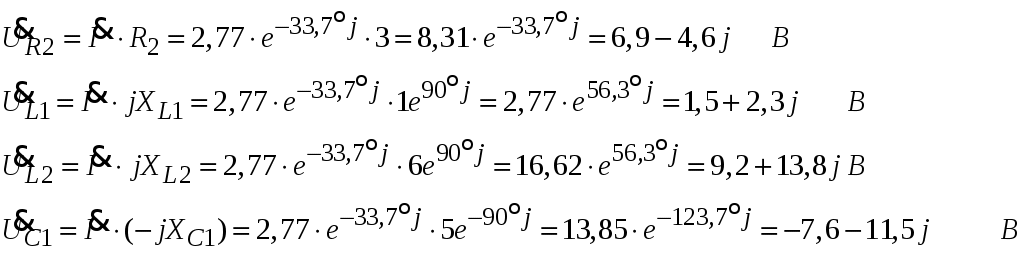 Построим векторную диаграмму тока и напряжений Масштаб : 1 клетка=2 В,1 клетка=0,5А 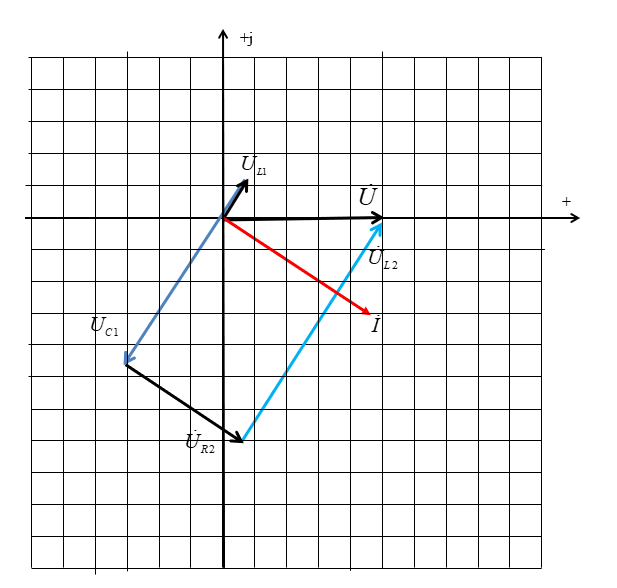 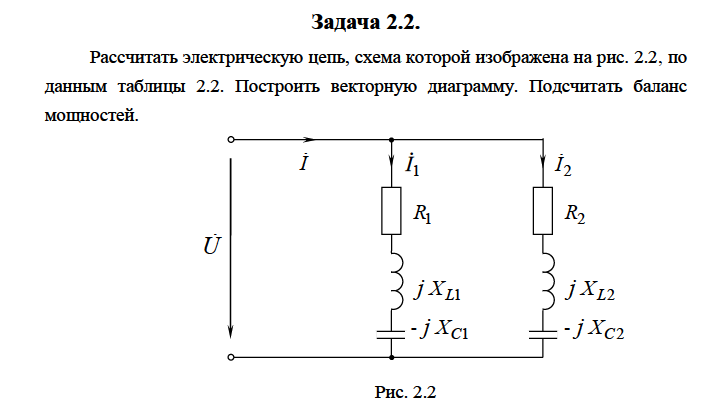  Решение Изобразим схему согласно варианта 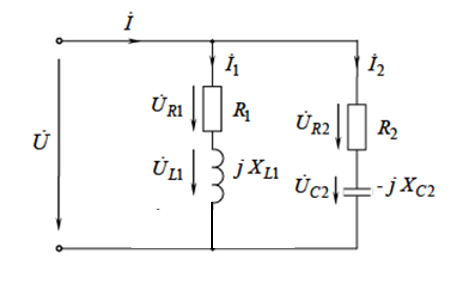 Определим комплексное сопротивление для каждой ветви по формуле: 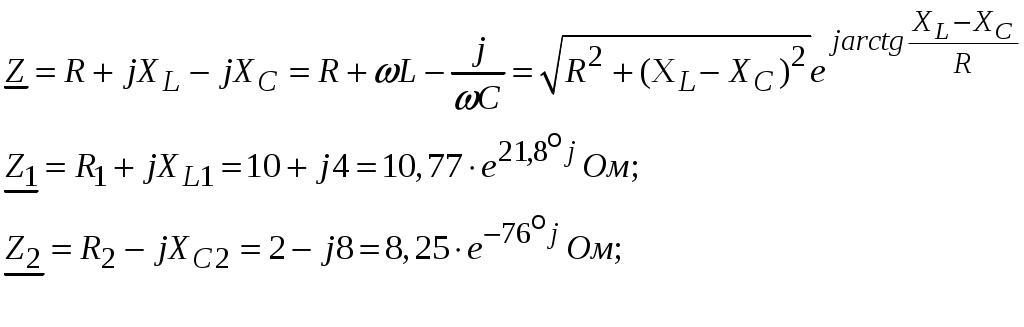 Определим полное комплексное сопротивление всей схемы в целом: 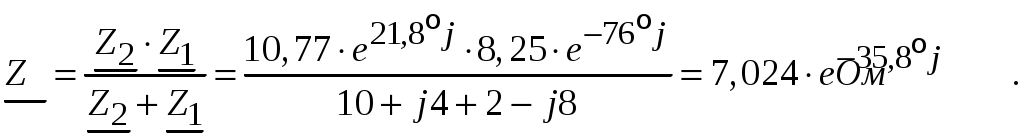 Выражаем заданное входное напряжение в комплексной форме ( если начальная фаза ЭДС источника не задана, то принимаем ее равной нулю): Определим комплексное значение тока в каждой ветви: 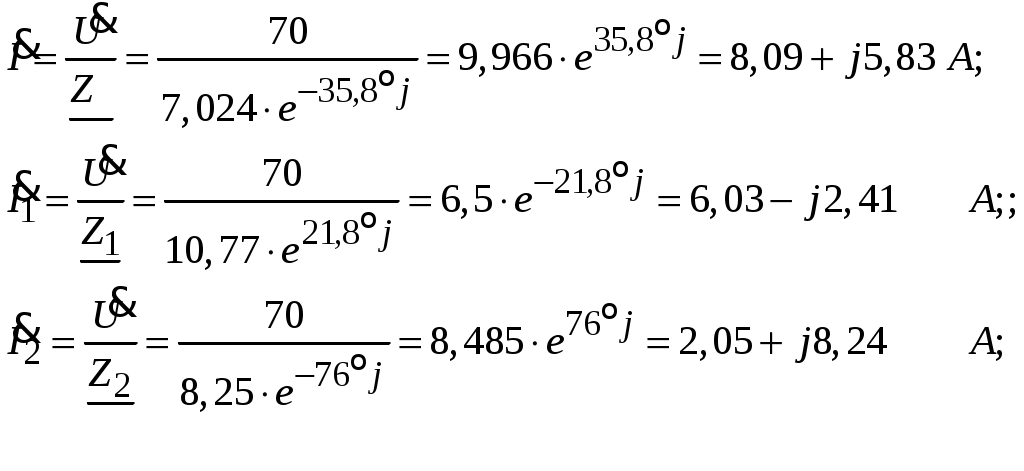 Действующие значения токов : 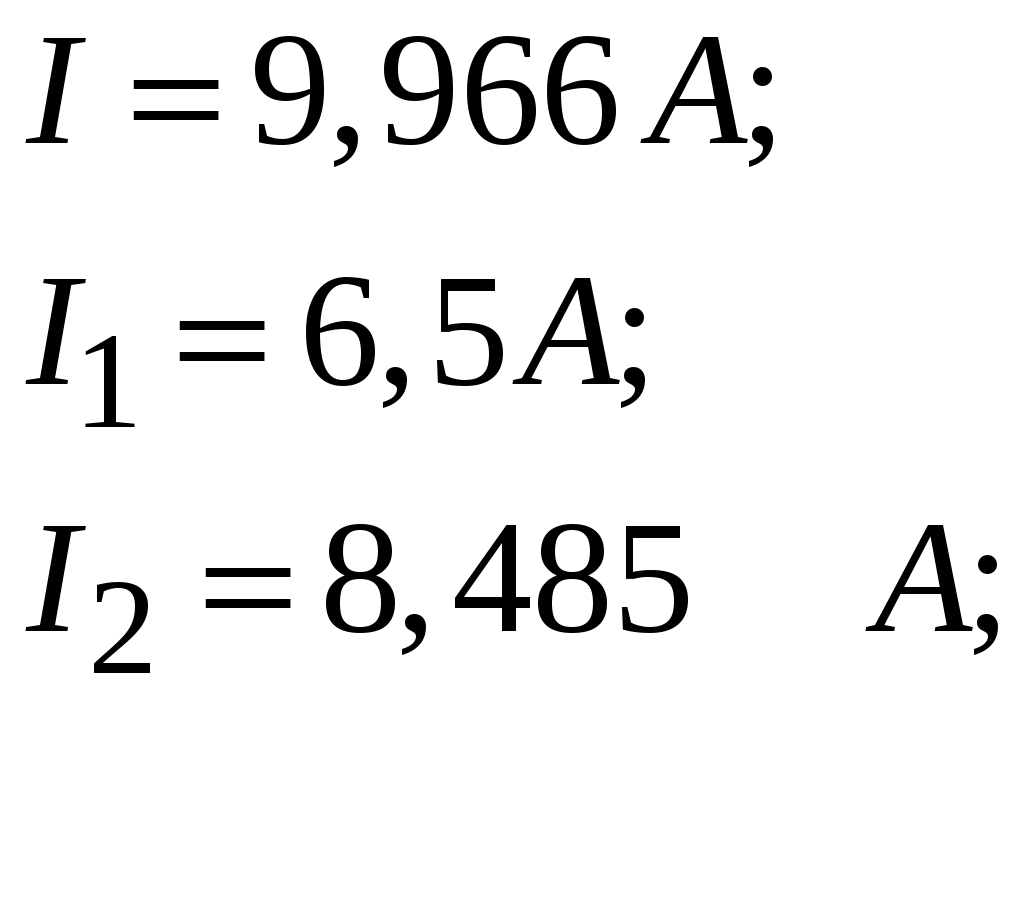 Составим уравнение баланса мощности Согласно балансу мощности в цепи синусоидального тока: Полная комплексная мощность источника : где S –полная мощность источника. - активная мощность потребителя - реактивная мощность потребителя: Полная мощность источников соответственно равна: 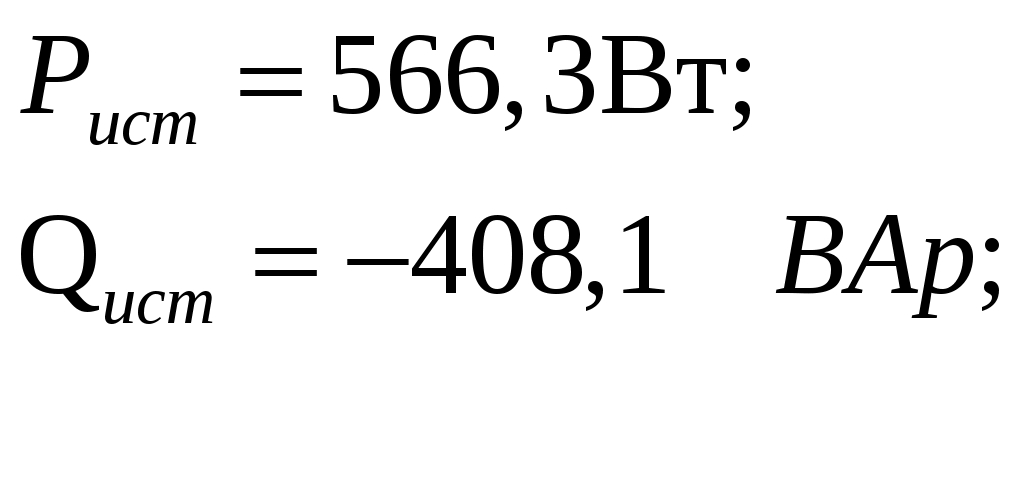 Баланс мощности в цепи соблюдается в пределах допустимой погрешности. Для построения в комплексной плоскости векторной диаграммы токов и напряжений и необходимо определить падение напряжения на каждом отдельном элементе схемы: 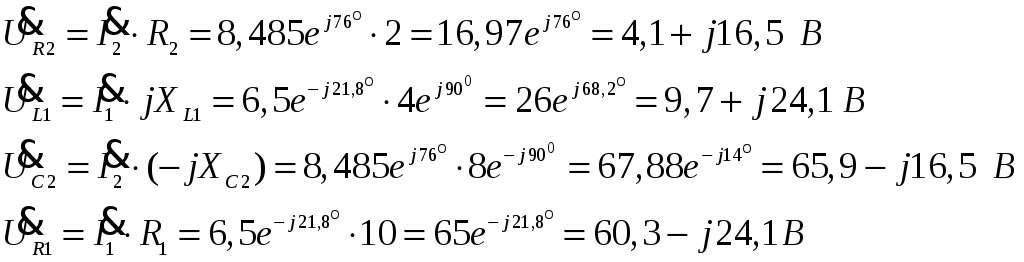 Масштаб: 1 клетка = 10 В, 1 клетка =1 А 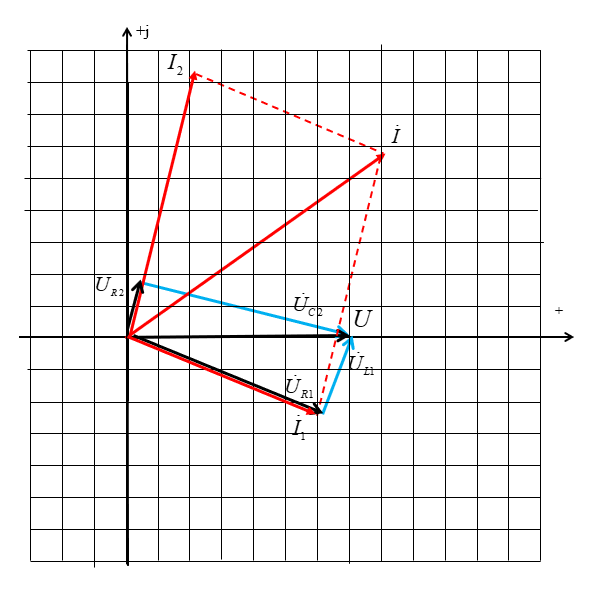 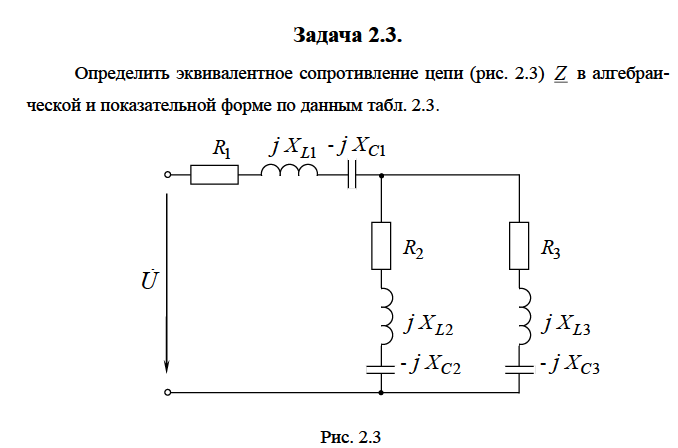   Решение: Изобразим схему согласно варианта 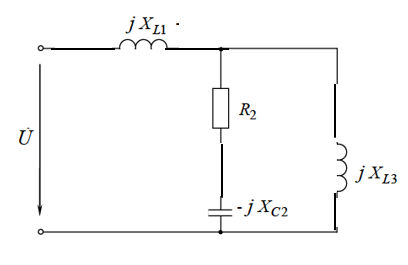 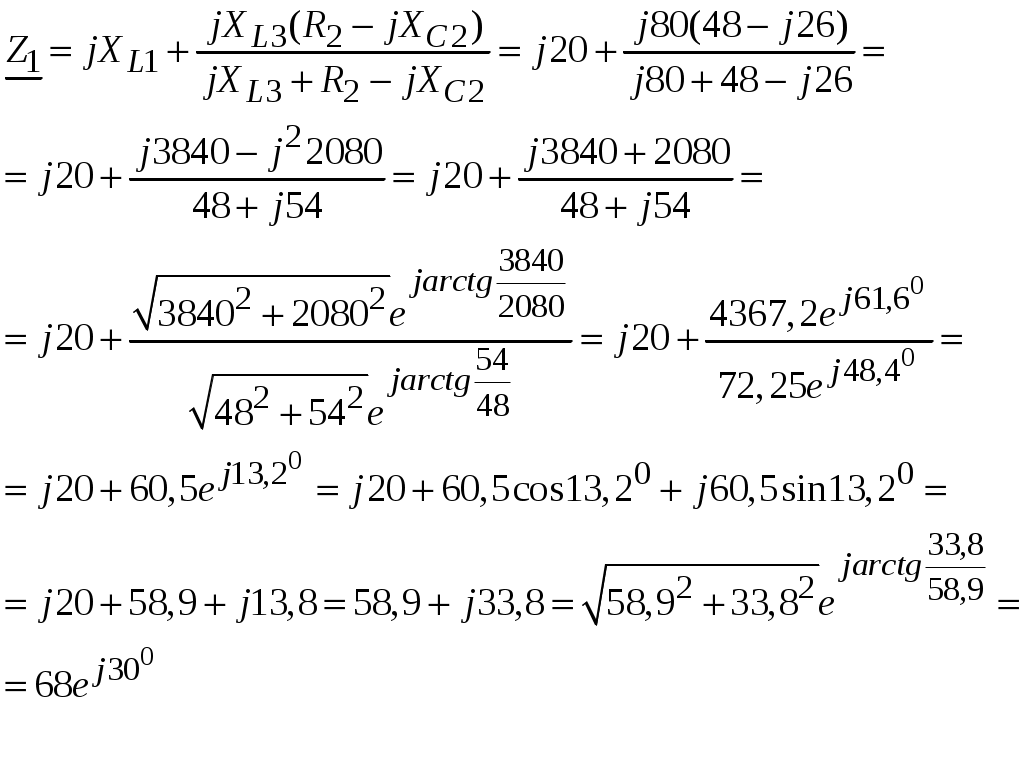 |
