кр. КР электротех. Контрольная работа по дисциплине Электротехника
 Скачать 287.2 Kb.
|
|
| Электроёмкостью двух проводников называют отношение заряда одного из проводников к разности потенциалов между ними:  |
Электроёмкость уединённого проводника равна отношению заряда проводника к его потенциалу, если все другие проводники бесконечно удалены и потенциал бесконечно удалённой точки равен нулю.
Чем больше электроёмкость, тем больший заряд скапливается на проводниках при одном и том же напряжении. Обратим внимание, что сама электроёмкость не зависит ни от сообщённых проводникам зарядов, ни от возникающего между ними напряжения.
Единицей электроёмкости в СИ является фарад.
Из-за того что заряд в 1 Кл очень велик, ёмкость 1 Ф оказывается очень большой. Поэтому на практике часто используют доли этой единицы: микрофарад (мкФ) — 10-6 Ф и пикофарад (пФ) — 10-12 Ф.
Конденсатор представляет собой два проводника, разделённые слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Простейший плоский конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга (рис. 14.39).
| Е  сли заряды пластин одинаковы по модулю и противоположны по знаку, то силовые линии электрического поля начинаются на положительно заряженной обкладке конденсатора и оканчиваются на отрицательно заряженной. Поэтому почти всё электрическое поле сосредоточено внутри конденсатора и однородно. |
Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника напряжения, например к полюсам батареи аккумуляторов. Можно также первую обкладку соединить с полюсом батареи, у которой другой полюс заземлён, а вторую обкладку конденсатора заземлить. Тогда на заземлённой обкладке останется заряд, противоположный по знаку и равный по модулю заряду незазем- лённой обкладки. Такой же по модулю заряд уйдёт в землю.
Заземление проводников — это соединение их с землёй (очень большим проводником) с помощью металлических листов в земле, водопроводных труб и т. д.
Под зарядом конденсатора понимают абсолютное значение заряда одной из обкладок.
Электроёмкость конденсатора определяется формулой (14.22).
Электрические поля окружающих тел почти не проникают внутрь конденсатора и не влияют на разность потенциалов между его обкладками. Поэтому электроёмкость конденсатора практически не зависит от наличия вблизи него каких-либо других тел.
Электроёмкость плоского конденсатора. Геометрические характеристики плоского конденсатора полностью определяются площадью S его пластин и расстоянием d между ними. От этих величин и должна зависеть ёмкость плоского конденсатора.
Чем больше площадь пластин, тем больший заряд можно на них накопить: q S. Напряжение же между пластинами согласно формуле (14.21, с. 314) пропорционально расстоянию между ними. Поэтому ёмкость
Кроме того, ёмкость конденсатора зависит от свойств диэлектрика между пластинами. Так как диэлектрик ослабляет поле, то электроёмкость при наличии диэлектрика увеличивается:
где ε — диэлектрическая проницаемость диэлектрика.Определение э.д.с. самоиндукции
Основы электродинамики были заложены Ампером в 1820 году. Работы Ампера вдохновили многих инженеров на конструирование различных технических устройств, таких как электродвигатель (конструктор Б.С. Якоби), телеграф (С. Морзе), электромагнит, конструированием которого занимался известный американский ученый Генри.
Джозеф Генри прославился благодаря созданию серии уникальных мощнейших электромагнитов с подъемной силой от 30 до 1500 кг при собственной массе магнита 10 кг. Создавая различные электромагниты, в 1832 году ученый открыл новое явление в электромагнетизме – явление самоиндукции.
Генри изобретал плоские катушки из полосовой меди, с помощью которых добивался силовых эффектов, выраженных более ярко, чем при использовании проволочных соленоидов. Ученый заметил, что при нахождении в цепи мощной катушки ток в этой цепи достигает своего максимального значения гораздо медленнее, чем без катушки.
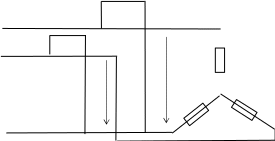
Опыт: На рисунке изображена электрическая схема экспериментальной установки, на основе которой можно продемонстрировать явление самоиндукции. Электрическая цепь состоит из двух параллельно соединенных лампочек, подключенных через ключ к источнику постоянного тока. Последовательно с одной из лампочек подключена катушка. После замыкания цепи видно, что лампочка, которая соединена последовательно с катушкой, загорается медленнее, чем вторая лампочка.
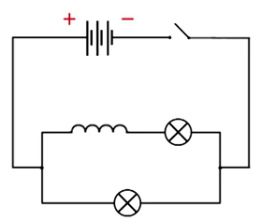
При отключении источника лампочка, подключенная последовательно с катушкой, гаснет медленнее, чем вторая лампочка.
Рассмотрим процессы, происходящие в данной цепи при замыкании и размыкании ключа.
1. Замыкание ключа.
В цепи находится токопроводящий виток. Пусть ток в этом витке течет против часовой стрелки. Тогда магнитное поле будет направлено вверх.
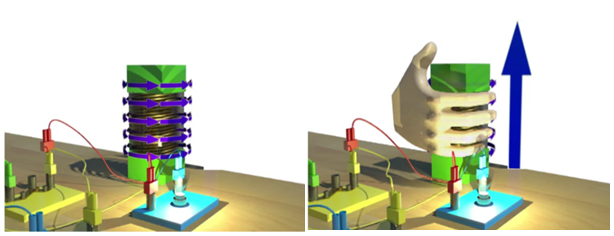
Таким образом, виток оказывается в пространстве собственного магнитного поля. При возрастании тока виток окажется в пространстве изменяющегося магнитного поля собственного тока. Если ток возрастает, то созданный этим током магнитный поток также возрастает. Как известно, при возрастании магнитного потока, пронизывающего плоскость контура, в этом контуре возникает электродвижущая сила индукции и, как следствие, индукционный ток. По правилу Ленца этот ток будет направлен таким образом, чтобы своим магнитным полем препятствовать изменению магнитного потока, пронизывающего плоскость контура.
То есть, для рассматриваемого на рисунке 4 витка индукционный ток должен быть направлен по часовой стрелке, тем самым препятствуя нарастанию собственного тока витка. Следовательно, при замыкании ключа ток в цепи возрастает не мгновенно, благодаря тому, что в этой цепи возникает тормозящий индукционный ток, направленный в противоположную сторону.
2. Размыкание ключа.
При размыкании ключа ток в цепи уменьшается, что приводит к уменьшению магнитного потока сквозь плоскость витка. Уменьшение магнитного потока приводит к появлению ЭДС индукции и индукционного тока. В этом случае индукционный ток направлен в ту же сторону, что и собственный ток витка. Это приводит к замедлению убывания собственного тока.
Вывод: при изменении тока в проводнике возникает электромагнитная индукция в этом же проводнике, что порождает индукционный ток, направленный таким образом, чтобы препятствовать любому изменению собственного тока в проводнике. В этом заключается суть явления самоиндукции. Самоиндукция – это частный случай электромагнитной индукции.
Самоиндукция – это явление возникновения электромагнитной индукции в проводнике при изменении силы тока, протекающего сквозь этот проводник.
Индуктивность. Модуль вектора индукции В магнитного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф В I.
Можно, следовательно, утверждать, что
Ф = LI,
где L — коэффициент пропорциональности между током в проводящем контуре и магнитным потоком.
Величину L называют индуктивностью контура, или его коэффициентом самоиндукции.
Используя закон электромагнитной индукции и полученное выражение, получаем равенство
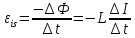
если считать, что форма контура остается неизменной и поток меняется только за счет изменения силы тока.
Из формулы следует, что индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на 1 А за 1 с.
Индуктивность, подобно электроемкости, зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Очевидно, что индуктивность одного проволочного витка меньше, чем у катушки (соленоида), состоящей из N таких же витков, так как магнитный поток катушки увеличивается в N раз.
Единицу индуктивности в СИ называют генри (обозначается Гн). Индуктивность проводника равна 1 Гн, если в нем при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В:
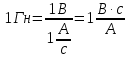
С явлением самоиндукции человек сталкивается ежедневно. Каждый раз, включая или выключая свет, мы тем самым замыкаем или размыкаем цепь, при этом возбуждая индукционные токи. Иногда эти токи могут достигать таких больших величин, что внутри выключателя проскакивает искра, которую мы можем увидеть.
Аналогия между самоиндукцией и инерцией. Явление самоиндукции подобно явлению инерции в механике. Так, инерция приводит к тому, что под действием силы тело не мгновенно приобретает определенную скорость, а постепенно. Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила. Точно так же за счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы не прекращаем ток сразу. Самоиндукция поддерживает его некоторое время, несмотря на сопротивление цепи.
1.3 Мощности в цепи переменного тока
Ранее рассматривались энергетические соотношения в отдельных элементах r, L и C при синусоидальном токе.
Разберем теперь более общий случай участка электрической цепи, напряжение на котором равно U = Umsin ωt, а ток
I= Imsin (ωt– φ).
Мгновенная мощность, поступающая в цепь,
P= UmImsin (ωt) sin (ωt– φ)
(3.26)
состоит из двух слагаемых: постоянной величины UIcos φ и синусоидальной, имеющей удвоенную частоту по сравнению с частотой напряжения и тока.
Среднее значение второго слагаемого за время Т, в течение которого она совершает два цикла изменений, равно нулю, поэтому активная мощность, поступающая в рассматриваемый участок цепи,
Множитель cos φ носит название коэффициента мощности. Активная мощность равна произведению действующих значений напряжения и тока, умноженному на коэффициент мощности.
Чем ближе угол φ к нулю, тем ближе cos φ к единице и, следовательно, тем большая при заданных значениях U и I активная мощность передается источником приемнику.
Повышение коэффициента мощности промышленных электроустановок представляет важную технико-экономическую задачу.
Выражение активной мощности может быть преобразовано с учетом (3.18) и (3.24):
P = z I2 cos φ = rI2, P= yU2 cos φ = gU2 .
Активная мощность может быть также выражена через активную составляющую напряжения (Ua = Ucos φ) или активную составляющую тока (Ia = Icos φ):
P= UaI, P= UIa.
Согласно (3.26) мгновенная мощность колеблется с удвоенной угловой частотой 2ω относительно линии, отстоящей от оси времени на P = UI cos φ.
В промежутки времени, когда Uи Iимеют одинаковые знаки, мгновенная мощность положительна; энергия поступает от источника в приемник, поглощается в сопротивлении и запасается в магнитном поле индуктивности.
В электрических системах, в которых источниками электрической энергии являются генераторы переменного тока, мощность получается от первичных двигателей, приводящих генераторы во вращение. В радиотехнике и электронике, где синусоидальные колебания создаются с помощью электронных или полупроводниковых приборов, мощность получается от источников постоянного тока, питающих электронные генераторы или другого рода устройства.
Величина, равная произведению действующих тока и напряжения,
S= U
(3.28)
называется полной мощностью и измеряется в вольт-амперах (ВА). Следует заметить, что амплитуда синусоидальной составляющей мгновенной мощности численно равна полной мощности.
На основании (3.27) и (3.28) коэффициент мощности равен отношению активной мощности к полной:
cos φ = P/S.
При расчетах электрической цепи и на практике в эксплуатации пользуются также понятием реактивная мощность, которая вычисляется по формуле
Q= UIsin φ
и является мерой потребления (или выработки) реактивного тока. Эта мощность выражается в единицах, называемых вар. Очевидно
S2 = P2 + Q2, sin φ = Q/S, tg φ = Q/P.
Выражение реактивной мощности может быть преобразовано с учетом (3.18) и (3.24):
Q= zI2 sin φ = xI2, Q= yU2 sin φ = bU2.
Реактивная мощность может быть также выражена через реактивную составляющую тока (Ip = I sin φ) или реактивную составляющую напряжения (Up = U sin φ):
Q= UpI, Q= UIp.
В соответствии с принятым ранее правилом знаков для угла φ реактивная мощность положительна при отстающем токе (индуктивная нагрузка) и отрицательна при опережающем токе (емкостная нагрузка).
Понятия активная (средняя), реактивная и полная мощности являются удобными определениями мощностей, которые прочно укоренились на практике.
Реактивная мощность цепи, содержащей индуктивность и емкость, пропорциональна разности максимальных значений энергии, запасаемой в магнитном и электрическом полях:
Q= ω (WLmax – WCmax) (3.2)
1.4 Мощность трехфазной системы, измерение активной мощности в симметричной трехфазной системе.
Любую схему соединения нагрузки трехфазной цепи можно путем преобразований привести к эквивалентной схеме соединения «звездой».
Трехфазная электрическая цепь состоит из трех однофазных цепей (фаз), поэтому мощности трехфазной цепи можно определить суммой мощностей отдельных фаз.
Активная мощность трехфазной цепи
P= PΑ +PΒ+ PC, (141)
где РА, РВ, РС –активные мощности фаз А, В, С соответственно.
;
PА= UΑIΑcosφΑ;
PВ= U
ВIВ
cosφВ
(142)
PС= UСIСcosφС,
При симметричной нагрузке
PΑ= PΒ
= PC
= UФIФcosφ. (143)
При этом условии с учетом выражений (127), (128), (139), (140) и (141) активная мощность трехфазной цепи
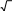P= 3UФIФcosφ= 3UЛIЛcosφ. (144)Аналогичным образом определяются реактивная и полная мощности трехфазной цепи.
Реактивная мощность трехфазной цепи
Q= QΑ= QΒ= QC, (145)
где QА, QВ, QС –реактивные мощности фаз А, В, С соответственно.
;
QА= UΑIΑsin φΑ;
QВ= U
ВIВ
sin φВ
(146)
QС= UСIСsin φС.
При симметричной нагрузке
QΑ= QΒ
= QC
= UФIФsin φ. (147)
При этом условии с учетом выражений (127), (128), (139), (140) и (145) реактивная мощность трехфазной цепи
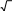Q= 3UФIФsin φ= 3UЛIЛsin φ. (148)Полная мощность трехфазной цепи
S= . (149)Полная мощность при симметричной нагрузке
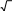S= 3UФIФ= 3UЛIЛ. (150) 
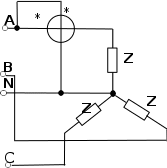Для измерения мощности трехфазной системы применяют различные схемы включения ваттметров. При симметричной нагрузке в четырехпроводной цепи активную мощность можно
Рис. 48. Измерение активной мощности одним ваттметром
измерить одним ваттметром, включенным по схеме, изображенной на рис. 48.
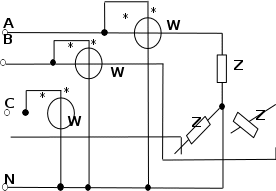
Рис. 49. Измерение активной мощности тремя ваттметрами
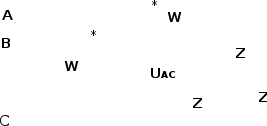
в трехфазной четырехпроводной цепи при несимметричной нагрузке*
Рис. 50. Измерение активной мощности двумя ваттметрами в трехфазной трехпроводной цепи при симметричной и несимметричной нагрузках
В трехпроводных трехфазных цепях при симметричной и несимметричной нагрузках широко применяют схему измерения мощности при помощи двух ваттметров.
Список использованных источников
1. Данилов И.Л., Иванов П.М. Общая электротехника с основами электроники.–М.: Высшая школа. – 2000. – 752 с.
2. Евдокимов Ф. Е. Теоретические основы электротехники.–М.: Высшая школа, 1999. – 496 с.
3. Касаткин А.С., Немцов М.В. Электротехника.–М.: Высшая школа, 2003. – 542 с.
4. Лоторейчук Е.А. Теоретические основы электротехники.–М.: Высшая школа. – 2000. – 224 с.
5. Третьяк Г.М., Тихонов Ю.Б. Электрические цепи переменного тока: Учебное пособие. – Омск: Изд-во СибАДИ, 2004. – 84 с.
6. Атабеков Г. И. Теоретические основы электротехники / Г. И. Атабеков. М.: Энергия, 1978. 592 с.
7. Иванов И. И. Электротехника / И. И. Иванов, А. Ф. Лукин, Г. И. Соловьев. СПб. : Лань, 2002. 192 с.
8. Рекус Г. Г. Общая электротехника и основы промышленной электроники : учебное пособие для вузов / Г. Г. Рекус. М. : Высшая школа, 2008. 654 с.
9. Гоноровский И. С. Радиотехнические цепи и сигналы : учебник для вузов / И. С. Гоноровский. М. : Сов. радио, 1987. 608 с.
10. Попов В. П. Основы теории цепей / В. П. Попов. М. : Высшая школа, 2000. 356 с.