ФИЗИКА КОНТРОЛЬНАЯ. Контрольная работа по дисциплине Физика Вариант 5 студент заочного обучения 2 курса
 Скачать 216.75 Kb. Скачать 216.75 Kb.
|
|
Министерство сельского хозяйства Российской Федерации Иркутский государственный аграрный университет имени А.А.Ежевского Контрольная работа по дисциплине «Физика» Вариант №5 Выполнил: студент заочного обучения 2 курса Энергетического факультета По специальности Электроэнергетика и электротехника Швец М.А. № зачетной книжки 207595 Проверил: к.т.н, доцент Вржащ Е.Э. Иркутск 2022 Контрольная работа №1 Задание №105 Материальная точка движется прямолинейно. Уравнение движения имеет вид xAtBt3, где A3м с; B0,06м с3. Найти скорость и ускорение точки в моменты времени t1 0 и t2 3c. Каковы средние значения скорости и ускорения за первые 3с движения?
Задание №118 Человек массой 70 кг, бегущий со скоростью 9 км/ч, догонят тележку массой 190 кг, движущуюся со скоростью 3,6 км/ч, и вскакивает на нее. С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
Ответ: V2’ - -1,56 м/с Задание №128 Спутник вращается вокруг Земли по круговой орбите радиусом 1700 км. Определить его линейную скорость и период обращения, если радиус Земли равен 6400 км.
Ответ: V - 7 км/с, Т – 121 мин Задание №138 Вычислить кинетическую энергию вала диаметром 0,3 м, вращающегося с частотой 200 об/мин, если масса его 2·103 кг.
Ответ: Ek – 4914,1 Дж Задание №148 Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению  , где А = 2 рад/с, В = 0,2 рад/с3. Определить вращающий момент, действующий на стержень через 2 с после начала вращения, если момент инерции стержня , где А = 2 рад/с, В = 0,2 рад/с3. Определить вращающий момент, действующий на стержень через 2 с после начала вращения, если момент инерции стержня  . .
Ответ: М – 0,115 Н∙м Задание №158 Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых 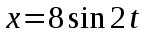 и и  . Написать уравнение траектории и построить ее. Показать направление движения точки. . Написать уравнение траектории и построить ее. Показать направление движения точки.
Контрольная работа №2 Задание №208 Вычислить плотность азота, находящегося в баллоне под давлением 2 МПа и имеющего температуру 400 К.
Ответ: ρ – 16,8 кг/м3 Задание №218 Давление идеального газа 10 мПа, концентрация молекул 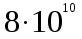 см-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа. см-3. Определить среднюю кинетическую энергию поступательного движения одной молекулы и температуру газа.
Ответ: Т – 9000К, Еk – 1,863∙10-19 Дж Задание №228 Средняя квадратичная скорость некоторого газа при нормальных условиях равна 480 м/с. Сколько молекул содержит 1 г этого газа?
Ответ: N – 2,04∙1022 молекул Задание №238 Найти молярную массу среды, для которой удельная изобарная теплоемкость сp = 1820 Дж/( 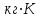 ) и изохорная cv = 1360 Дж/( ) и изохорная cv = 1360 Дж/(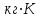 ). ).
Ответ: М – 0,018 кг/моль Задание №248 Водород массой 4 г был нагрет на  при постоянном давлении. Определить работу расширения газа. при постоянном давлении. Определить работу расширения газа.
Ответ: А – 166,2 Дж Задание №258 Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Определить: 1) термический КПД цикла; 2) отношение температур нагревателя и холодильника.
Ответ: η – 20%, Т1/Т2 – 1,25 Контрольная работа №3 Задание №308 Расстояние l между зарядами Q 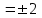 нКл равно 25 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r1 = 15 см от первого и на расстоянии r2 = 20 см от второго заряда. нКл равно 25 см. Определить напряженность Е поля, созданного этими зарядами в точке, находящейся на расстоянии r1 = 15 см от первого и на расстоянии r2 = 20 см от второго заряда. 
Ответ: Е – 2,14∙103 В/м Задание №318 Пылинка массой 0,2 мг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость 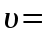 10 м/с. Определить скорость 10 м/с. Определить скорость 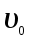 пылинки до того, как она влетела в поле. пылинки до того, как она влетела в поле.
Ответ: V1 – 9,996 м/с Задание №328 Плоский воздушный конденсатор заряжен до разности потенциалов 300 В. Площадь пластин S = 1см2, напряженность поля в зазоре между ними Е = 300 кВ/м. Определить поверхностную плотность заряда на пластинах, емкость и энергию конденсатора.
Ответ: σ – 2,7∙10-6 Кл/м2, С – 8,85∙10-13 Ф, W – 3,9825∙10-8 Дж Задание №338 Определить плотность тока в железном проводнике длиной 10 м, если провод находится под напряжением 6 В, удельное сопротивление железа  = 98 нОм·м. = 98 нОм·м.
Ответ: j – 6,1∙106 А/м2 Задание №348 ЭДС батареи аккумуляторов равна 12 В, сила тока короткого замыкания равна 5 А. Какую наибольшую мощность можно получить во внешней цепи, соединенной с такой батареей?
Ответ: Рmax – 15 Вт Контрольная работа №4 Задание №408 По кольцевому медному проводнику протекает ток 30 А. В центре контура с током создается магнитное поле напряженностью 30 А/м. Определить разность потенциалов на концах проводника, если его поперечное сечение 3 мм2. Удельное сопротивление меди 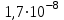 Ом·м. Ом·м.
Ответ: U – 0,534 В Задание №418 Контур из провода, изогнутого в форме квадрата со стороной, а = 0,5м, расположен в одной плоскости с бесконечным прямолинейным проводом с током I = 5 А так, что две его стороны параллельны проводу. Сила тока в контуре I1 = 1 А. Определить силу, действующую на контур, если ближайшая к проводу сторона контура находится на расстоянии b = 10 см.
Ответ: F – 4,17 мкН Задание №428 В плоскости, перпендикулярной однородному магнитному полю напряженностью 2·105 А/м вращается стержень длиной 0,4 м относительно оси, проходящей через его середину. В стержне индуцируется электродвижущая сила, равная 0,2 В. Определить угловую скорость стержня.
Ответ: ω - -20(с-1) Задание №438 На дифракционную решетку, содержащую 500 штрихов на 1 мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину спектра первого порядка на экране, если расстояние L от линзы до экрана равно 3 м. Границы видимого спектра λкр. = 780 нм, λф = 400 нм.
Ответ: b – 0,57 м Задание №448 На поверхность металла падает монохроматический свет с длиной волны 0,1 мкм. Красная граница фотоэффекта 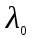 = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
Ответ: 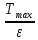 – 66,7% – 66,7%Задание №458 Постоянная радиоактивного распада  для изотопа для изотопа 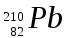 равна 10-9 с-1. Определить время, в течение которого распадается 2/5 начального количества ядер этого радиоактивного изотопа. равна 10-9 с-1. Определить время, в течение которого распадается 2/5 начального количества ядер этого радиоактивного изотопа.
Ответ: t – 16,176 лет Задание№468 Вычислить энергию ядерной реакции 
Ответ: Е – 2,73 МэВ |





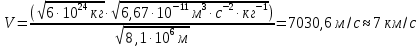

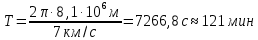
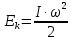 , где
, где  – угловая скорость вала
– угловая скорость вала



 , где М – вращающий момент,
, где М – вращающий момент,  –
– 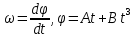 тогда
тогда
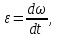 тогда
тогда 
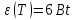
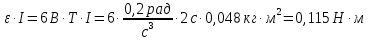
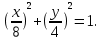 Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория эллипс. Теперь найдем направление движения. В момент t=0 получаем:
Из этого уравнения видно, что радиус эллипса вдоль x равен 8см, а вдоль y равен 4см. Итак, траектория эллипс. Теперь найдем направление движения. В момент t=0 получаем:
 , Р – давление азота, V – объем сосуда, Т – температура газа, R = 8,31 Дж/(моль∙К) – молярная газовая постоянная.
, Р – давление азота, V – объем сосуда, Т – температура газа, R = 8,31 Дж/(моль∙К) – молярная газовая постоянная.

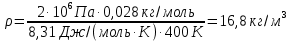

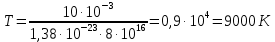
 где k – постоянная Больцмана, k = 1,38∙10-23Дж/К, i – количество степеней свободы.
где k – постоянная Больцмана, k = 1,38∙10-23Дж/К, i – количество степеней свободы.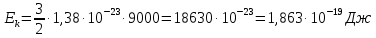
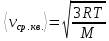
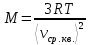
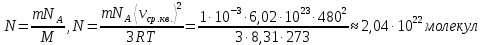


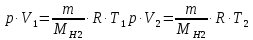

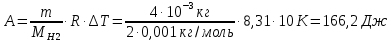

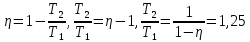

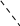




























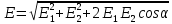
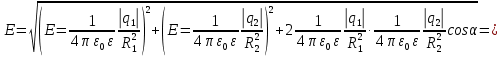

 – начальная кинетическая энергия пылинки, W=Q∙U – потенциальная энергия пылинки, проходящей через разность потенциалов U,
– начальная кинетическая энергия пылинки, W=Q∙U – потенциальная энергия пылинки, проходящей через разность потенциалов U,  – конечная кинетическая энергия пылинки.
– конечная кинетическая энергия пылинки. , откуда искомая скорость
, откуда искомая скорость 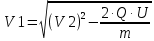


 (Кл/м2)
(Кл/м2)
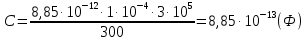

 где
где 


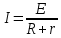
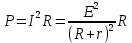

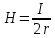


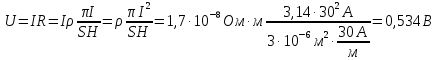




 при повороте на угол dφ пересечет площадь
при повороте на угол dφ пересечет площадь  а весь стержень пересечет площадь
а весь стержень пересечет площадь 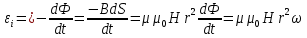


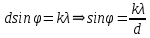
 , где d – период дифракционной решетки, который можно найти, зная длину решетки l и число штрихов на решетке n.
, где d – период дифракционной решетки, который можно найти, зная длину решетки l и число штрихов на решетке n.



 энергия фотона. Откуда Tmax=ε-A.
энергия фотона. Откуда Tmax=ε-A. - красная граница фотоэффекта.
- красная граница фотоэффекта.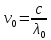 (c – скорость света), тогда
(c – скорость света), тогда  – работа выхода из металла.
– работа выхода из металла.
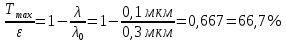


 .
. ,
, с или t = 16,176 лет.
с или t = 16,176 лет. -10,0129
-10,0129 -7,0160
-7,0160 -4,0026
-4,0026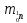 -1,0086
-1,0086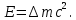
 равен разности масс продуктов, вступающих в реакцию и полученных в результате реакции:
равен разности масс продуктов, вступающих в реакцию и полученных в результате реакции:
