кр по компьютерной правткие. КР_по_КП_СафароваАА_11ИПдФК2. Контрольная работа по дисциплине Компьютерный практикум Вариант 10 Преподаватель доцент, к т. н. Исхаков З. Ф
 Скачать 164.42 Kb. Скачать 164.42 Kb.
|
|
Федеральное государственное образовательное бюджетное учреждение высшего образования ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ Уфимский филиал Кафедра «Математики и информатики» КОНТРОЛЬНАЯ РАБОТА по дисциплине «Компьютерный практикум» Вариант № 10 Преподаватель: доцент, к.т.н. Исхаков З.Ф. Работа выполнена: Сафарова А.А. направление «Экономика» профиль «Финансы и кредит» группа 11ИПдФК2 № студенческой книжки: 100.28/200970 Уфа – 2021 Содержание Стр.Задания 2 Введение 4 Заключение 15 Список используемой литературы 16 ЗаданияПосчитать сколько дней рождений выпадает на среду в зависимости от даты вашего дня рождения. Дата рождения: 30.01.1989 г. Дана формула линейной функции: y=b + ax. Известно, что а=10, b=20. Протабулировать функцию на интервале значений x от 1 до 10 с шагом 1. С помощью инструмента Подбор параметра, изменяя значение b определить, чему равен y в точке x=10, если в точке x=6 значение y=100. С щагом 0,1 и 0,01 изобразить на плоскости графики функций 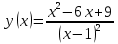 , , 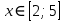 Найти первую производную функции 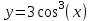 в точке в точке 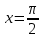 . .ВведениеExcel - это пакет программ, разработанный фирмой Microsoft для работы в среде Windows. Этот пакет позволяет автоматизировать учрежденческую, производственную или научную деятельность, связанную со сбором, хранением, переработкой, передачей и использованием информации. Многие документы (планы работ, ведомости, справки, отчеты, счета, финансовые документы и т.п.) для наглядности представляют текстовые и числовые данные в табличной форме. Для автоматизации работы с ними служат специальные программы (точнее пакеты программ), называемые процессорами электронных таблиц (ЭТ) по названию используемого в них метода представления и обработки данных, одной из которых и является пакет программ Excel. В чем заключается преимущество электронной таблицы по сравнению с обычным бумажным представлением данных? 6 Во-первых, в нее легче вводить данные, используя операцию копирования для занесения аналогичных данных в ячейки, строки, столбцы и даже в целые прямоугольные области таблицы. Во-вторых, копировать можно не только данные, но и соотношения между ними, задаваемые с помощью формул и функций. В-третьих, ЭТ является эффективным средством для моделирования различных вариантов и ситуаций. Меняя значения исходных параметров, например, данных в отдельных ячейках таблицы, можно сразу увидеть, как это сказывается на конечных результатах, зависящих от изменяемых данных. В-четвертых, сформированная и записанная в дисковую память электронная таблица становится документом многократного использования: ее можно выводить на печать в любом количестве экземпляров, представлять различные соотношения между данными в графической форме, модифицировать таблицу и использовать ее в качестве основы для создания других таблиц. Целью данной работы является получение практических навыков работы с Excel. Задание 1 Посчитать, сколько дней рождений выпадает на среду в зависимости от даты вашего дня рождения (30.01 1989 г). Заполним данные в таблицу по всем годам с указанием даты рождения по сегодняшний день при помощи функции автозаполнения. Получаем список с датами рождения по годам (рис.1). 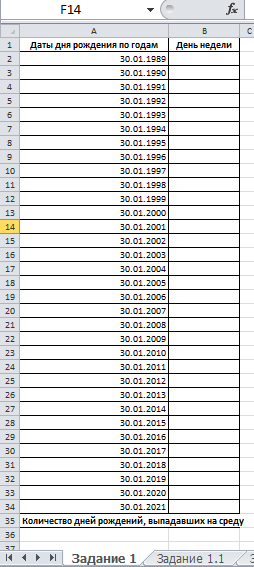 Рис. 1. Таблица с заполненными датами Делаем на новом листе таблицу соответствия дня недели и номера ( рис.2) 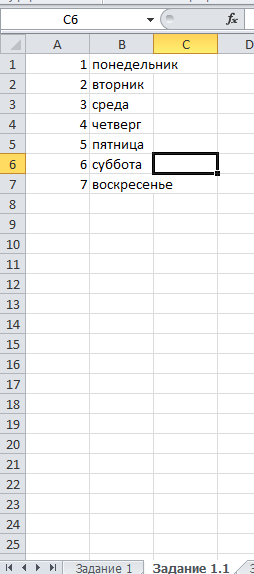 Рис.2. Таблица соответствия номера дня недели и названия. С помощью функций ВПР и ДЕНЬНЕД создаем формулу, по которой сначала будет найден номер дня недели, соответствующий дате дня рождения, а потом номер будет переведен в название дня недели. Затем с помощью функции СЧЁТЕСЛИ в ячейке В35 находим количество сред. Ответ 5. С помощью условного форматирования выделяем среды желтой заливкой. (рис.3). 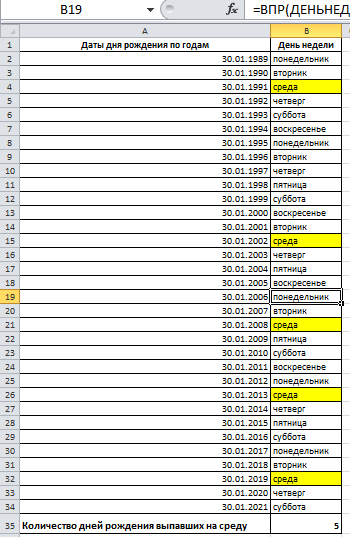 Рисунок 3. Количество дней рождения выпавших на среду. Задание 2 Дана формула линейной функции: y=b + ax. Известно, что а=10, b=20. Про табулировать функцию на интервале значений xот 1 до 10 с шагом 1. С помощью инструмента Подбор параметра, изменяя значение b определить, чему равен y в точке x=10, если в точке x=6 значение y=100. Сделаем таблицу исходных данных, и внесем данные x [1;10], с помощью функции суммы заполним таблицу (рис.4). 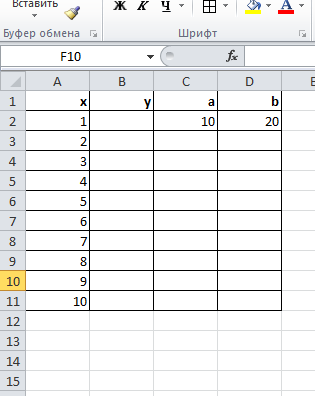 Рисунок 4. Таблица исходных данных. С помощью формулы заполним столбец y (рис.5) 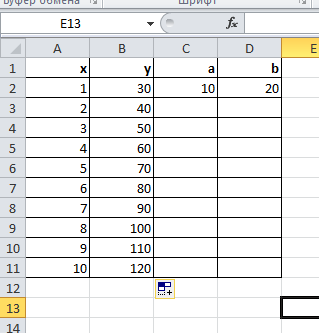 Рисунок 5. Таблиц с данными y при x [1;10]. Заполним таблицу исходных данных для подбора параметра (рис.6). 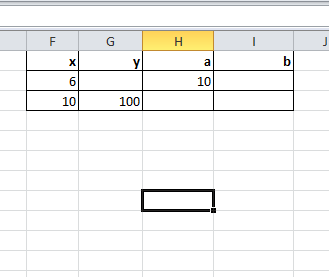 Рисунок 6. Таблица исходных данных для подбора параметра. Использую формулу исходных данных в ячейки G2 и G3 забиваем формулы. Потом с помощью функции подбор данных получаем ответ, при x=10, y=140, при этом значение b=40 (рис.7). 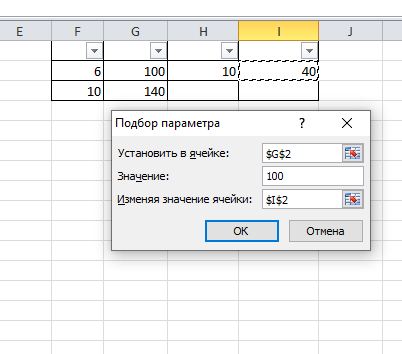 Рисунок 7. Таблица с формулами и функция подбор параметра. Задание 3 С шагом 0,1 и 0,01 изобразить на плоскости графики функций 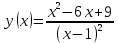 , , 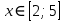 Составим таблицу для табулирования первой функции с шагом 0,1. В ячейку А2 введем значение 2, в ячейку А3 – формулу =A2+0,1. Скопируем формулу до конца диапазона. В ячейку В2 введем формулу =(A2^2-6*A2+9)/(A2-1)^2. Скопируем формулу до конца диапазона. Выделим полученную таблицу и выберем команду Вставка / Диаграмма. Выберем тип диаграммы. Результат изображен на рисунке 8. 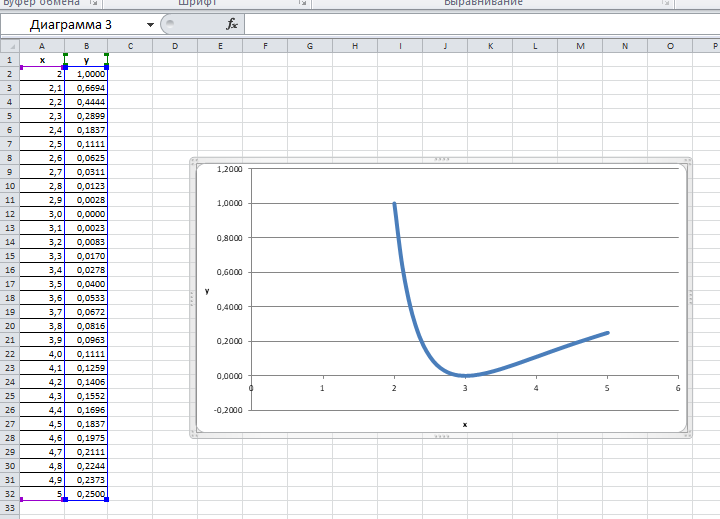 Рисунок 8. Функция с шагом 0,1 Аналогично построим таблицу и график функции с шагом 0,01 на другом листе (рис. 9). 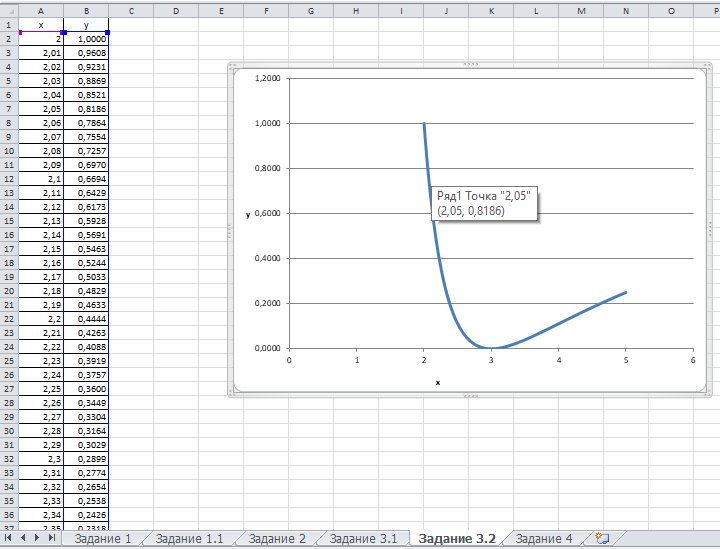 Рис. 9. Функция с шагом 0,01 Задание 4 Найти первую производную функции 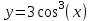 в точке в точке 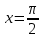 . .Вводим в ячейку С3 рабочего листа заданное значение аргумента формулой =ПИ()/2, в ячейке С4 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке С5 вычисляем сумму =С3+С4 (рис. 10). 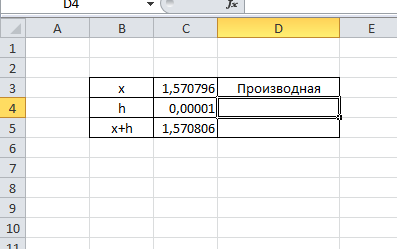 Рисунок 10. Данные для вычисления производной Формулу для вычисления производной подставляем в ячейку D4: =(3*COS(C6)^3)-(3*COS(C4)^3)/C5. 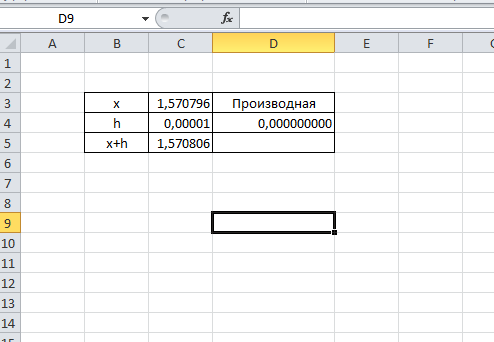 Рисунок 11. Поиск производной по формуле ЗаключениеТак было доказано, что Excel одна из удобнейших программ для решение табличных заданий и составлений графиков. Были показаны некоторые возможности данной программы, путем решения заданий. Список используемой литературыГобарева Я.Л., Городецкая О.Ю., Золотарюк А.В. Бизнес-аналитика средствами Excel: Учебное пособие. - М.: Вузовский учебник: ИНФРА-М, 2014. – 336с. (ЭБС Znanium) Киселев Г.М. Информационные технологии в экономике и управлении (эффективная работа в MS Office 2007) [Электронный ресурс]: Учебное пособие / Г.М. Киселев, Р.В. Бочкова, В.И. Сафонов. - М.: Издательско-торговая корпорация "Дашков и К°", 2013. - 272 с. (ЭБС Znanium) Я.Л. Гобарева, О.Ю. Городецкая, А.В. Золотарюк Введение в Excel: Учебно-методические рекомендации для проведения семинара №1 «Excel как калькулятор» по дисциплине «Компьютерный практикум» для бакалавров направления 38.03.01 «Экономика». - М.: Электронное издание, 2017. – 15 с. Т.Л. Фомичева, М.Б. Хрипунова Математические операции, вычисление значений функций, подбор параметра под заданное значение. (Excel): Учебно-методические рекомендации для проведения семинара №2 «Excel как калькулятор» по дисциплине «Компьютерный практикум» для бакалавров направления 38.03.01 «Экономика». - М.: Электронное издание, 2017. – 24 с. Г.С. Жукова, В.А. Иванюк Построение графиков функций в Excel: Учебно-методические рекомендации для проведения семинара №3 по компьютерному практикуму для бакалавров направления 38.03.01 «Экономика». - М.: Электронное издание, 2017. – 39 с. Р.М. Магомедов, Е.В. Маевский Приближенное вычисление поведения функций вблизи точек разрыва. Графическое построение наклонных асимптот (Excel): Учебно-методические рекомендации для проведения семинара №4 по компьютерному практикуму для бакалавров направления 38.03.01 «Экономика». - М.: Электронное издание, 2017. – 14 с. |
