Математика ТулГУ 1 семеср. КР_Волкова Е.А.. Контрольная работа по дисциплине Математика Семестр 1 Вариант 1 студент гр. Иб360821
 Скачать 61.99 Kb. Скачать 61.99 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Интернет-институт КОНТРОЛЬНАЯ РАБОТА по дисциплине «Математика» Семестр 1 Вариант 1 Выполнил: студент гр. ИБ360821 Волкова Евгения Александровна Проверил: д.ф.-м.н., проф. Христич Д.В. Тула 2022 Задание 1. Для определителя 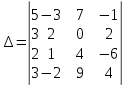 найти дополнительный минор элемента a34. найти дополнительный минор элемента a34.Решение: 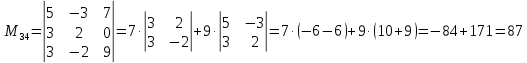 а34 = (-1)3+4·М34= -1·87 = -87 Ответ: -87. Задание 2. Найти матрицы [AB], [BA], [A-1], если [A]= 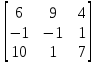 , [B]= , [B]=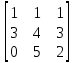 . .Решение: а) [AB] = 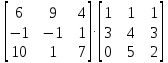 = == 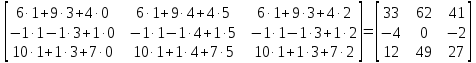 . .б) [BA]= 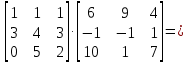 = 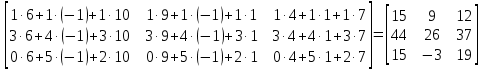 . .в) Для нахождения обратной матрицы используем метод присоединенной матрицы в соответствии с формулой: 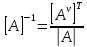 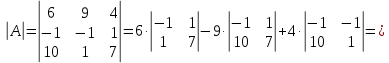 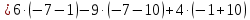 =-48+154+36=141 =-48+154+36=141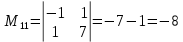 ; ; 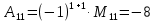 . .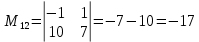 ; ; 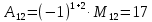 . .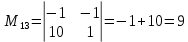 ; ; 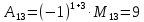 . .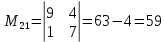 ; ; 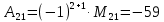 . .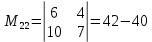 =2; =2; 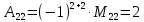 . .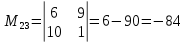 ; ; 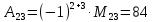 . .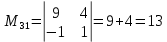 ; ; 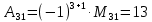 . .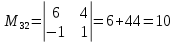 ; ; 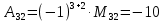 . .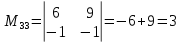 ; ; 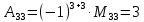 . .Запишем присоединенную матрицу: 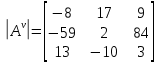 Транспонируем присоединенную матрицу: 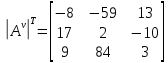 Запишем обратную матрицу: 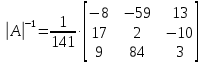 Ответ: а) 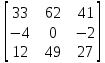 ; б) ; б) 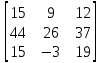 ; в) ; в) 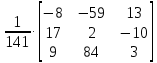 . .Задание 3. Проверить совместность системы уравнений и в случае совместности решить ее по правилу Крамера.  3х1 – 2х2 + 4х3 = 21 3х1 – 2х2 + 4х3 = 213х1 + 4х2 – 2х3 = 9 2х1 – х2 – х3 = 10 Решение: Запишем матрицу системы и найдем ее ранг: 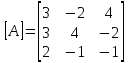 Найдем минор второго порядка: 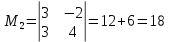 Так как М2≠0, то [А] имеет ранг не менее 2. Найдем определитель матрицы [А]: 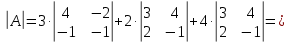 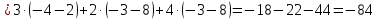 Так как 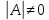 , то ранг [А] = 3. , то ранг [А] = 3.Запишем расширенную матрицу: 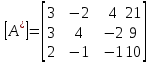 Найдем минор второго порядка: 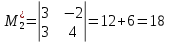 Так как 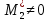 , то [А*] имеет ранг не менее 2. , то [А*] имеет ранг не менее 2.Найдем минор третьего порядка: 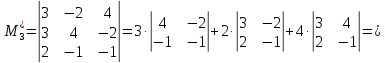 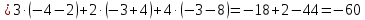 Так как 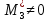 , то ранг [А*] равен 3. , то ранг [А*] равен 3.RgA = RgA* = 3, значит, по теореме по теореме Кронекера-Капелли система совместна. Решим систему по правилу Крамера: 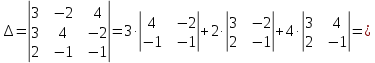 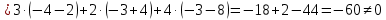 , значит система имеет единственное решение. , значит система имеет единственное решение.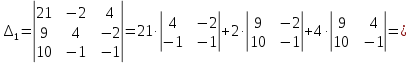 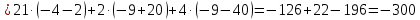 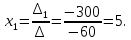 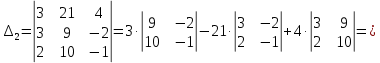 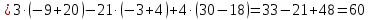 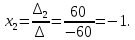 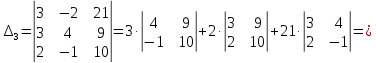 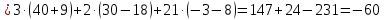 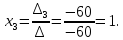 Ответ: x1=5; x2= -1; x3=1. Задание 4. Доказать, что векторы 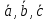 образуют базис, и найти координаты вектора образуют базис, и найти координаты вектора 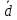 в этом базисе: в этом базисе: 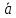 5,3,1, 5,3,1, 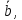 1,2,3, 1,2,3, 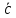 3,4,2, 3,4,2, 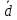 9,34,20. 9,34,20.Решение: Вычислим определитель, составленный из координат векторов 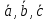 : :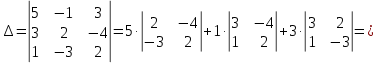 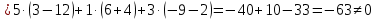 , значит, векторы , значит, векторы 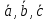 линейно независимы и образуют базис. линейно независимы и образуют базис.Представим вектор 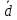 в виде линейной комбинации базисных векторов: в виде линейной комбинации базисных векторов: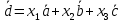 , , 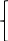 Или покоординатно: Или покоординатно:5х1 – х2 + 3х3= - 9 3х1 + 2х2 – 4х3= 34 х1 – 3х2 + 2х3= - 20 Решим систему по правилу Крамера: 63 0, значит, система имеет единственное решение. 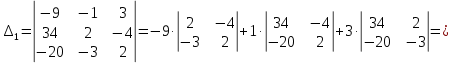 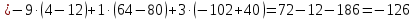 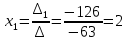 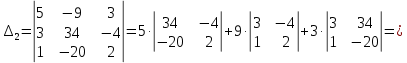 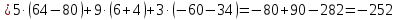 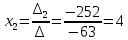 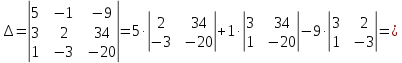 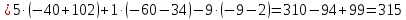 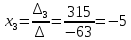 Ответ: векторы 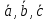 образуют базис, образуют базис, 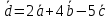 . .Задание 5. Вершины пирамиды находятся в точках А(3,−5,−2), В(−4,2,3), С(1,5,7), D(−2,−4,5). Найти объем пирамиды и длину высоты, опущенной из вершины В. Решение: a) Объем пирамиды равен: 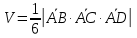 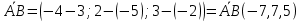 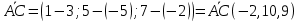 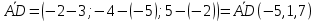 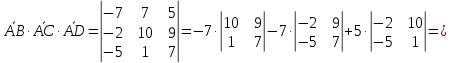 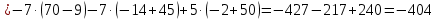 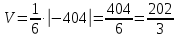 б) Объем пирамиды также равен 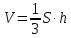 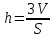 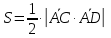 Найдем векторное произведение векторов: 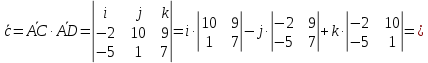 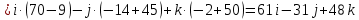 Найдем модуль вектора 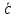 : :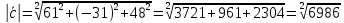 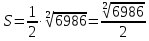 Найдем высоту: 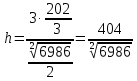 Ответ: 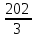 ед.3; ед.3; 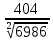 . .Задание 6. Найти расстояние от точки M0 до плоскости, проходящей через точки M1, M2, M3, если М1(1,3,6), М2(2,2,1), М3(-1,0,1), М0(5,-4,5). Решение: Запишем уравнение плоскости: 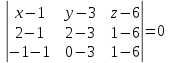 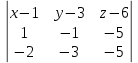 =0 =0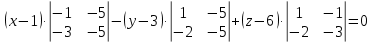 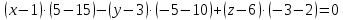 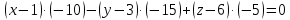 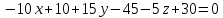 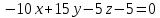 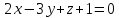 Найдем расстояние d от точки М0(5,-4,5) до плоскости 2х-3у+z+1=0 по формуле: 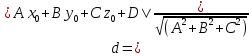 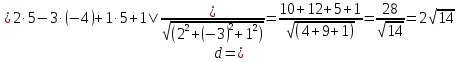 Ответ: 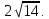 Задание 7. Написать канонические уравнения прямой 4x+y+z+2=0, 2x-y-3z-8=0 Решение: Прямая задана в виде пересечения двух плоскостей. Нормальные вектора плоскостей: 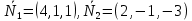 Прямая лежит в обеих плоскостях, следовательно перпендикулярна векторам 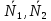 .То есть, вектор .То есть, вектор 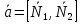 является направляющим вектором прямой. является направляющим вектором прямой. Найдём направляющий вектор: 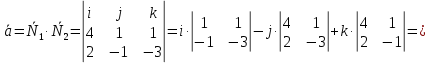 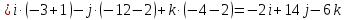 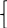 Выберем какую-нибудь точку на искомой прямой. Для этого найдём одно из решений системы уравнений: Выберем какую-нибудь точку на искомой прямой. Для этого найдём одно из решений системы уравнений:4x+y+z+2=0 2x-y-3z-8=0 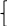 Примем z=0, Примем z=0,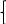 4х+у+2=0 у=-4х-2 4х+у+2=0 у=-4х-22х-у-8=0 2х-(-4х-2)-8=0 (1) 2х+4х+2-8=0 6х-6=0 у=-4·1-2 6х=6 у=-6 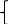 х=1 х=1 у=-6 Таким образом, прямая направлена вдоль вектора 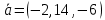 и проходит через точку Р0(1,-6,0). и проходит через точку Р0(1,-6,0).Её канонические уравнения принимают вид: 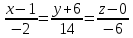 Ответ: 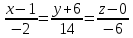 Задание 8. Найти точку пересечения прямой, заданной каноническими уравнениями, и плоскости 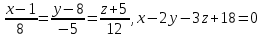 Решение: Запишем параметрические уравнения прямой: 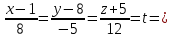  x=1+8t x=1+8ty=8 – 5t z=–5+12t Подставляем значения в уравнение плоскости: 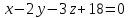 1+8t – 2(8 – 5t) – 3(– 5+12t)+18=0 1+8t–16+10t+15–36t+18=0 – 18t+18=0 t=1 Найдем координаты точки пересечения прямой и плоскости:  x=1+8·1=9 x=1+8·1=9y=8–5·1=3 z=–5+12·1=7 Таким образом, точка пересечения прямой и плоскости есть точка Р(9,3,7). Ответ: Р(9,3,7). Задание 9. Вычислить предел 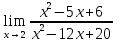 Решение: Разложим числитель и знаменатель на множители: 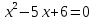 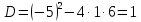 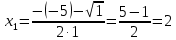 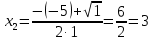 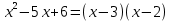 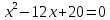 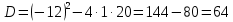 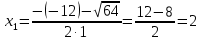 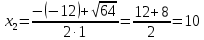 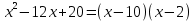 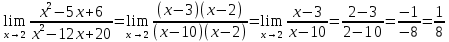 Ответ: 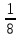 . .Задание 10. Вычислить предел 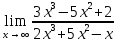 Решение: Разделим числитель и знаменатель на х3 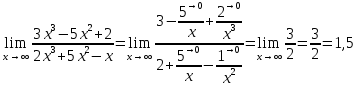 Ответ: 1,5. Задание 11. Вычислить предел 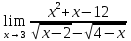 Решение: Разложим числитель на множители: 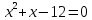 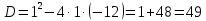 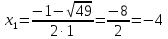 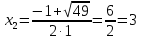 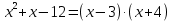 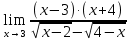 Домножим числитель и знаменатель на 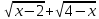 : :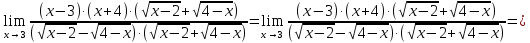 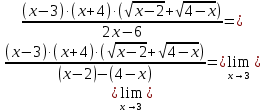 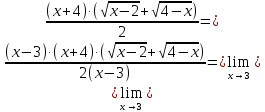 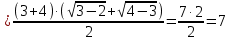 Ответ: 7. Задание 12. Вычислить предел 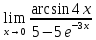 Решение: 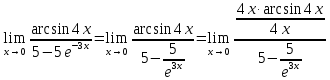 Используем первый замечательный предел 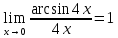 : :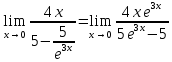 Используем свойство предела произведения: 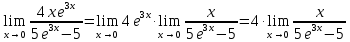 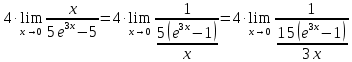 Используем формулу 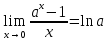 : :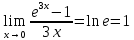 Получаем: 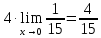 Ответ: 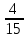 . .Задание 13. Вычислить предел 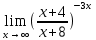 Решение: Преобразуем: 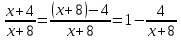 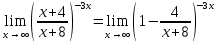 Преобразуем: 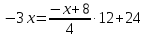 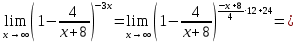 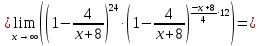 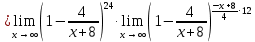 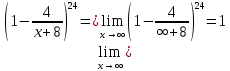 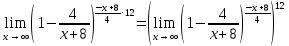 Используем второй замечательный предел 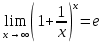 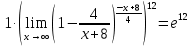 Ответ: е12. Задание 14. Составить уравнение нормали к данной кривой в точке с абсциссой х0 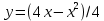 , x0=2. , x0=2.Решение: 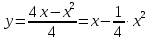 Найдём производную функции: 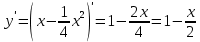 В точке х0=2: 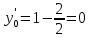 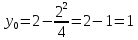 Уравнение нормали 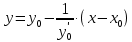 : :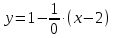 или или 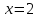 Ответ: 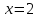 . .Задание 15. Найти дифференциал функции в точке с абсциссой х0 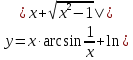 , x0=1. , x0=1.Решение: 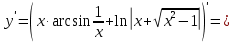 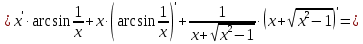 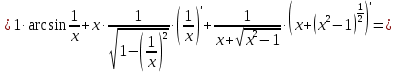 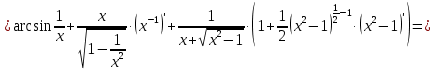 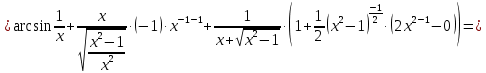 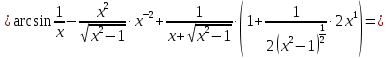 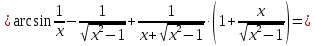 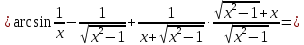 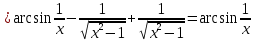 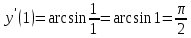 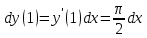 Ответ: 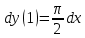 . . |
