Контрольная работа по математике 3 семестр. Контрольная работа по дисциплине Математика Семестр 3 Вариант 2 студент гр. Иб262501 Баранова А. Б
 Скачать 104.46 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Интернет-институт КОНТРОЛЬНАЯ РАБОТА по дисциплине «Математика» Семестр 3 Вариант 2 Выполнил: студент гр. ИБ262501 Баранова А.Б. Проверил: д.ф.-м.н., проф. Христич Д.В. 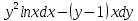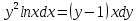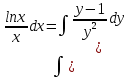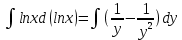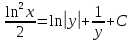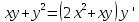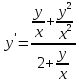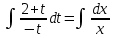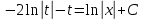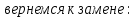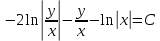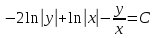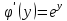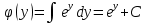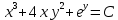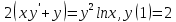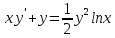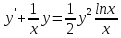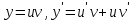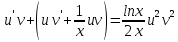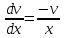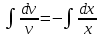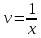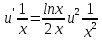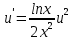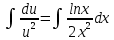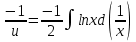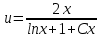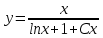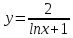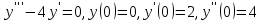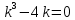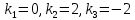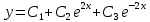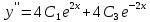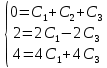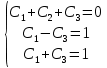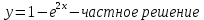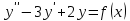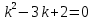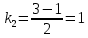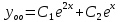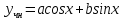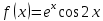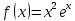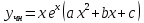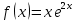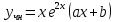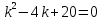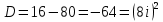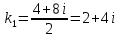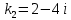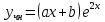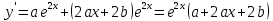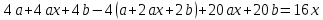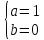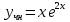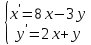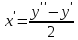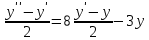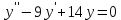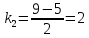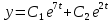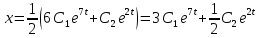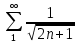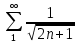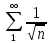Тула 2021 II вариант  Уравнение с разделяющимися переменными      Однородное дифференциальное уравнение  Замена:     dx       Уравнение полных дифференциалов     Ответ:   Уравнение Бернулли                        Общее решение:                                                         Ряд из модулей расходится по предельному признаку, т.к.: –расходится и Сам ряд сходится по признаку Лейбница, так как: 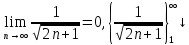 Вывод: исходный ряд сходится условно. 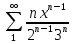 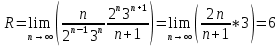  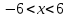  : 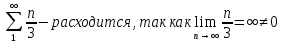 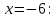 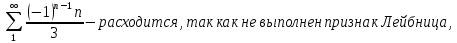 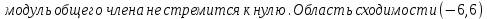 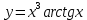 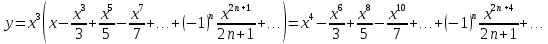14) Построим график соответственно числовым данным и запишем выражение для функции. 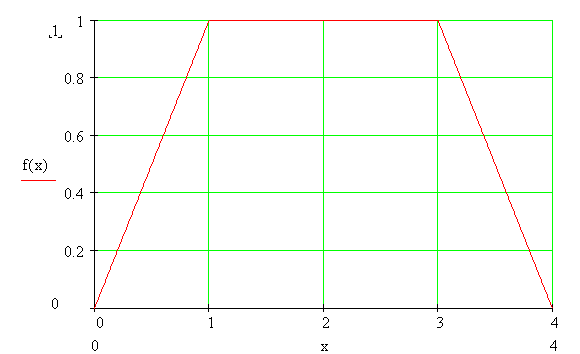 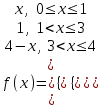 Так как функция чётная, то разложение будем делать по косинусам. Рассматриваем период от -4 до 4. Длина периода равна 8. Применяем расчётные формулы 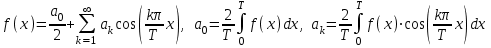 При вычислениях применяем табличный интеграл 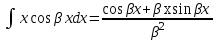 Вычисляем  Интеграл  равен площади трапеции 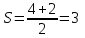 Тогда 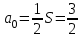  Вычисляем каждое слагаемое по отдельности     Складываем все 4 слагаемых (последнее со знаком минус) и по возможности упрощая запись, получим выражение для  в виде  Вычислим по этой формуле первые 10 коэффициентов. Получатся только 4 ненулевых коэффициента:  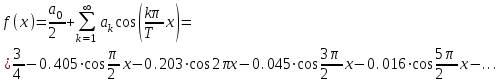 Строим график частичной суммы для 2, 3, 4 и 5 слагаемых полученного ряда вместе с графиком заданной функции на всём периоде от – 4 до 4. Для двух ненулевых слагаемых (гармоника одна) 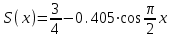  Для трёх ненулевых слагаемых (гармоник две)  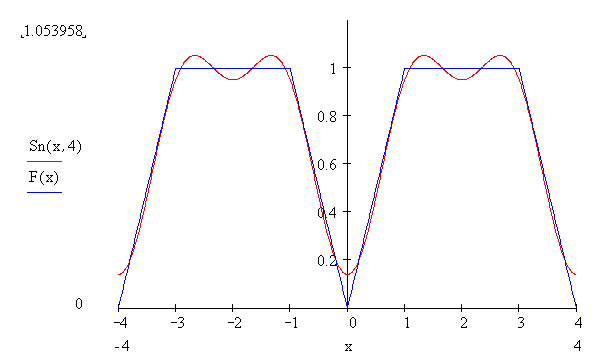 Для четырёх ненулевых слагаемых (гармоник три) 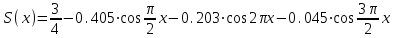  Для пяти ненулевых слагаемых (гармоник четыре) 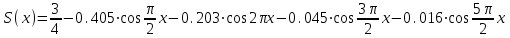 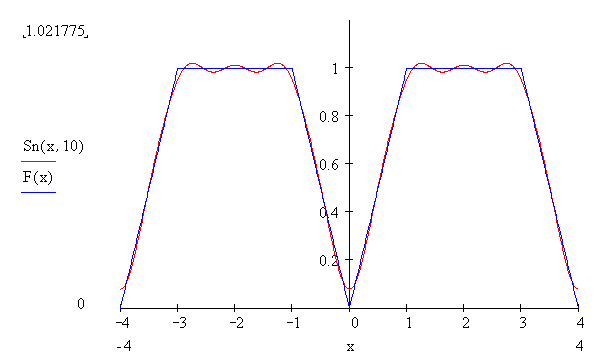 |