УРГЭУ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ. МАТЕМАТИКА. Контрольная работа по дисциплине Математика Зарипова Л. С. Помощь студентам

• Название: Контрольная работа по дисциплине Математика Зарипова Л. С. Помощь студентам
• Анкор: УРГЭУ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ
• Дата: 01.05.2023
• Размер: 0.86 Mb.
• Имя файла: МАТЕМАТИКА.docx
• Тип: Контрольная работа; #1099808

Министерство науки и ВЫСШЕГО ОБРАЗОВАНИЯ Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уральский государственный экономический университет» (УрГЭУ)

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Математика»
Зарипова Л.С. Помощь студентам. Автор.

Ват сап. [phone]

Институт непрерывного и дистанционного образования Направление подготовки ______________________ Направленность (профиль) __________________________________ Кафедра __________________________________ Дата защиты: ________________ Оценка: ________________

Студент ___________________________ Группа ____________________ Руководитель ___________________________ __________________ (ФИО, должность, звание)

Екатеринбург

2019 г.

2. Решение:

Для решения вычисления определителя приведем матрицу к верхнетреугольному виду, используя элементарные преобразования над строками матрицы и свойства определителя матрицы.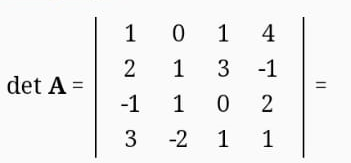



От 2 строки отнимаем 1 строку, умноженную на 2; к 3 строке добавляем 1 строку, умноженную на 1; от 4 строки отнимаем 1 строку. умноженную на 3.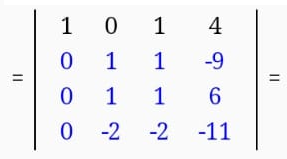


От 3 строки отнимаем 2 строку, умноженную на 1; к 4 строке добавляем 2 строку, умноженную на 2.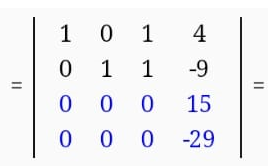



К четвертой строке добавляем 3 строку, умноженную на 29/15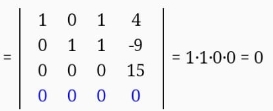



3. Решение: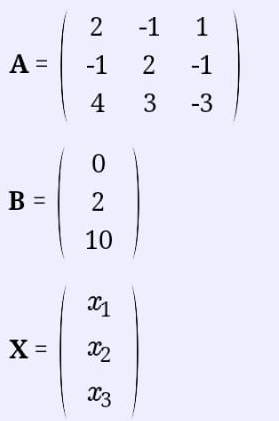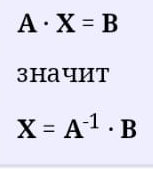





Найдем обратную матрицу методом алгебраических дополнений.

Найдем детерминант матрицы А:

Определитель матрицы А отличен от нуля. Следовательно, обратная матрица А-1 существует. Для вычисления обратной матрицы найдем дополнительные миноры и алгебраические дополнения матрицы А.

Найдем минор М11 и алгебраическое дополнение А11 . В матрице А вычеркиваем строку 1 и столбец 1.



Ниже покажем детальное вычисление определителя матрицы.



Найдем минор М12 и алгебраическое дополнение А12. В матрице А вычеркиваем строку 1 и столбец 2.





Найдем минор М13 и алгебраическое дополнение А13. В матрице А вычеркиваем строку и столбец 3.





Найдем минор М21 и алгебраическое дополнение А21. В матрице А вычеркиваем строку 2 и столбец 1.





Найдем минор М22 и алгебраическое дополнение А22. В матрице А вычеркиваем строку 2 и столбец 2.





Найдем минор М23 и алгебраическое дополнение А23. В матрице А вычеркиваем строку 2 и столбец 3.





Найдем минор М31 и алгебраическое дополнение А31. В матрице А вычеркиваем строку 3 и столбец 1.





Найдем минор М 32 и алгебраическое дополнение А32. В матрице А вычеркиваем строку 3 и столбец 2.





Найдем минор М33 и алгебраическое дополнение А33. В матрице А вычеркиваем строку 3 и столбец 3.





Выпишем союзную матрицу (матрицу алгебраических дополнений):



Транспонированная союзная матрица:



Найдем обратную матрицу:



Найдем решение: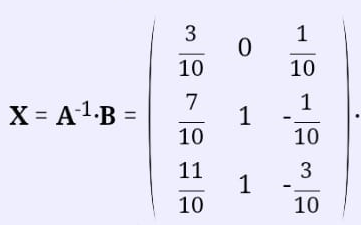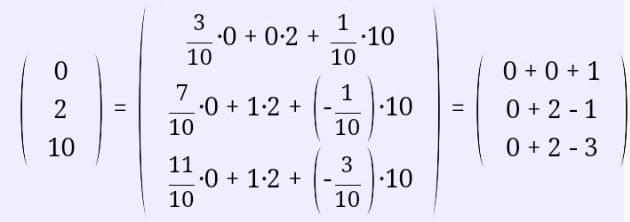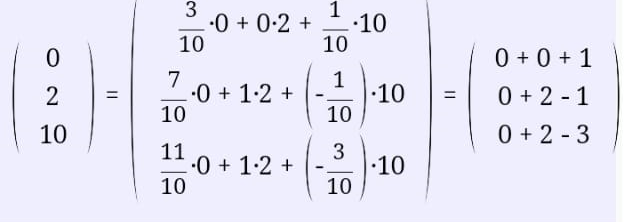







Ответ: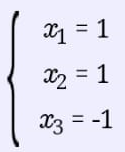



Решение: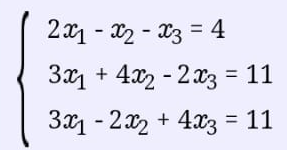



Перепишем систему уравнений в матричном виде и решим его методом Гаусса.



1ю строку делим на 2



От 2 строки отнимаем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 3.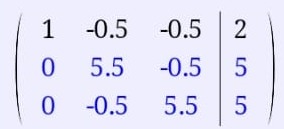



2 – ю строку делим на 5,5: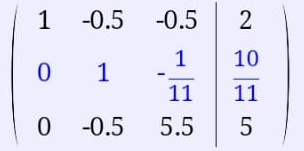



К 1 строке добавляем 2 строку, умноженную на 0,55; к 3 строке добавляем 2 строку, умноженную на 0,5.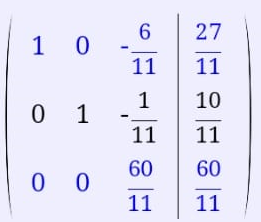



3ю строку делим на 60/11.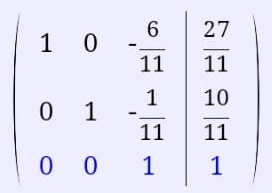



К 1 строке добавляем 3 строку, умноженную на 6/11; к 2 строке добавляем 3 строку, умноженную на 1/11.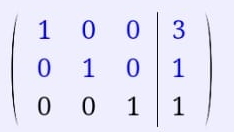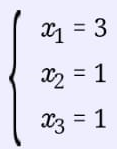





Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления:

2*3-1-1=61-1=4

3*3+4*1-2*1=9+4-2=11

3*3-2*1+4*1=9-2+4=11

Проверка выполнена успешно.