основы финансовых вычислений. Контрольная работа по дисциплине оценка и анализ рисков Вариант 2 Работу выполнила студентка Финансовокредитного факультета
 Скачать 442 Kb.
|
|
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ «ОЦЕНКА И АНАЛИЗ РИСКОВ» Вариант 2 Работу выполнила студентка Финансово-кредитного факультета Специальности финансы и кредит 5 курса, 2 В/О, л/д №05ФФД62052 Раскопова И.В. Работу проверила Преподаватель Зелепухина Е.Н. НОВОРОССИЙСК 2007ЗАДАЧА 1. В таблице 1 приведена информация о доходности акций по двум ценным бумагами и индекс рынка на протяжении пятнадцати кварталов. Требуется: 1. определить характеристики каждой ценной бумаги: а0,  , рыночный (или систематический) риск, собственный (или несистематический) риск, R2, .2. сформировать портфель минимального риска из двух видов ценных бумаг (табл.2) при условии, что обеспечивается доходность портфеля (mp) не менее чем по безрисковым ценным бумагам (облигациям) с учетом индекса рынка. 3. построить линию рынка капитала (СML); 4. построить линию рынка ценных бумаг (SML). Таблица 1
Решение: Построим модели доходности ценных бумаг (ГРАВ и РОЛП) от индекса рынка. Параметры модели найдем с помощью инструмента Регрессия Пакет анализа EXCEL. Для проведения регрессионного анализа выполним следующие действия: Выбераем команду Сервис - Анализ данных. В диалоговом окне Анализ данных выбераем инструмент Регрессия, а затем ОК. В диалоговом окне Регрессия в поле Входной интервал Y вводим адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал Х введим адреса одного или нескольких диапазонов, которые содержат значения независимых переменных. Результаты регрессионного анализа. А) по акциям ГРАВ.
Уравнение регрессии зависимости доходности ценной бумаги ГРАВ (m1) от индекса рынка mr имеет вид: m1 = 0,26 + 1,13*mr
Собственный (или несистематический) риск ценной бумаги ГРАВ (m1) равен: 12 = 2/N = 126,68/15 = 8,45 Рыночный (или систематический) риск равен 0,85. Это отношение характеризует долю риска данных ценных бумаг, вносимую рынком. Г 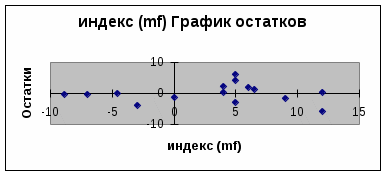 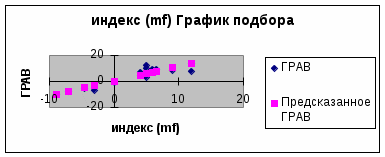 рафик регрессионной модели зависимости доходности акций ГРАВ от индекса рынка. Б) по акциям РОЛП.
Уравнение регрессии зависимости доходности ценной бумаги РОЛП (m2) от индекса рынка mr имеет вид: m2 = 2,0 + 0,73*mr
Собственный (или несистематический) риск ценной бумаги РОЛП (m2) равен: 22 = 2/N = 1158,19/15 = 77,21 Рыночный (или систематический) риск равен 0,21. Г 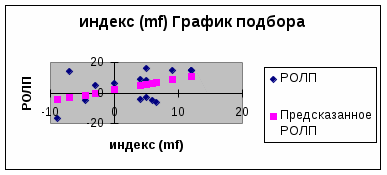 рафик регрессионной модели зависимости доходности акций РОЛП от индекса рынка. 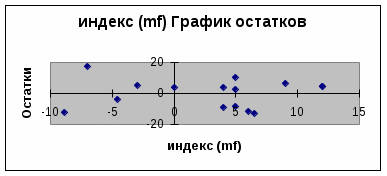 Решение оптимизационной задачи. Необходимо найти вектор Х= (X1, X2), минимизирующий риск портфеля p. решение задачи найдем в среде EXCEL с помощью надстройки Поиск решения. Воспользуемся алгоритмом Задачи Марковица о формировании портфеля заданной эффективности с учетом ведущего фактора и минимального риска, которая сформулирована следующим образом: Необходимо найти вектор Х= (X1, X2,… Xn), минимизирующий риск портфеля p. p =    Экономико-математическая модель задачи. X1 - доля в портфеле ценных бумаг ГРАВ; X2 - доля в портфеле ценных бумаг РОЛП. Имеем: По условию задачи задана эффективность портфеля не ниже, чем в среднем по облигациям, т.е. 2,73% (38,2/14=2,73%) – определяется как среднее значение доходности акций. 1 = 1,13, т.к. m1 = 0,26 + 1,13*mr 2 = 0,73 , т.к. m2 = 2,0 + 0,73*mr 12 = 8,45 22 = 77,21 Для вычисления  воспользуемся функцией ДИСПР вычисления дисперсии программного пакета EXCEL. Выделим область индексов рынка строки В2:В16. Найденное значение запишем в строке B19. = 38,51 Подставим в данную модель все известные значения и получим: p=  = minЗапишем ограничения: x1 + x2 = 1  x1 , x2 01. Введем все исходные данные в рабочий лист программного пакета EXCEL для поиска дальнейшего решения. 2. Введем подкоренное выражение: (((D25*D25*B24*B24+2*B24*B25*E25*D25+E25*E25*B25*B25)*B19)+ (D25*D25*B27)+(E25*E25*B28)) Для этого воспользуемся математической функцией КОРЕНЬ. 4. С помощью аналитической системы Поиск решений программного пакета EXCEL найдем оптимальное решение задачи: - зададим целевую ячейку; - установим указание на минимальное значение целевой функции; - зададим необходимые ограничения, согласно условию; - укажем дополнительно в параметрах неотрицательные значения. Найдено оптимальное решение.
Минимальный риск портфеля равный 7,1% при приемлемой доходности не менее 2,73% будут достигнут, если доля акций ГРАВ составит 0,72, а доля акций РОЛП составит 0,28. Построим линию рынка капитала (СML). Эта линия отражает зависимость риск – доходность, для портфелей, сочетающих рисковые и безрисковые активы. m 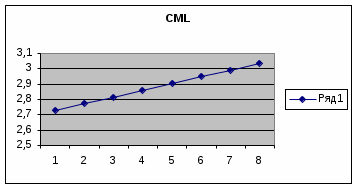 p= 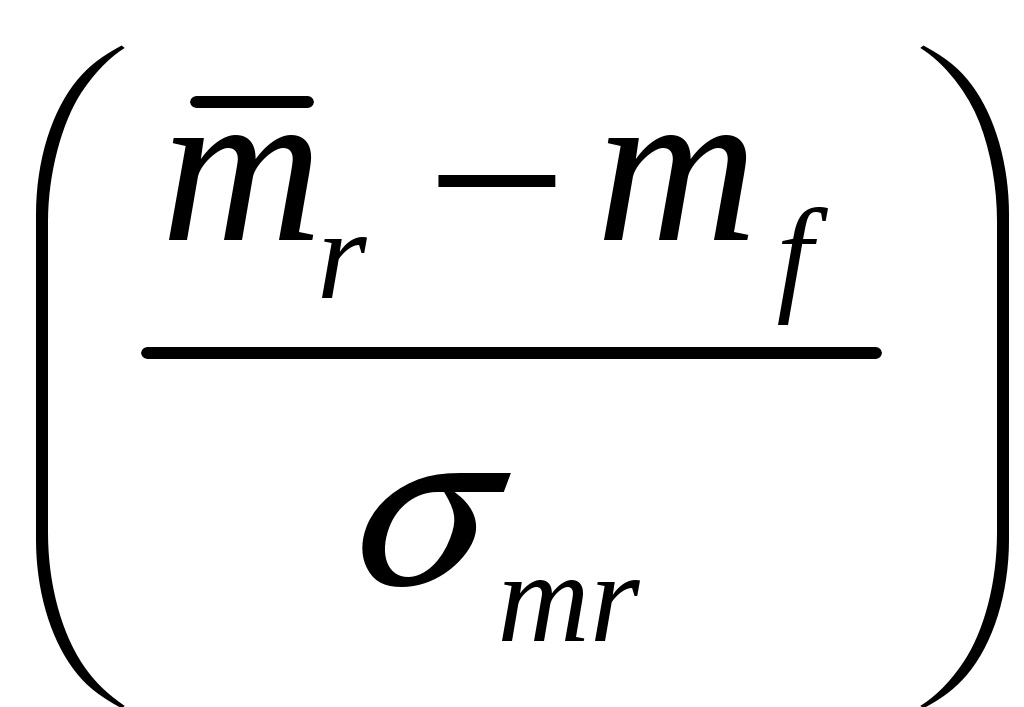 +  * =  = 3,04На графике CML по горизонтальной оси отложена доходность акций портфеля, по вертикальной – доходность рисковых ценных бумаг. Построим линию рынка ценных бумаг (SML). Связь между доходом ценной бумаги и ее бетта-коэффициентом линейная и называется линией рынка ценных бумаг SML. Уравнение SML может быть записано в форме:  В нашей задаче уравнение имеет вид: 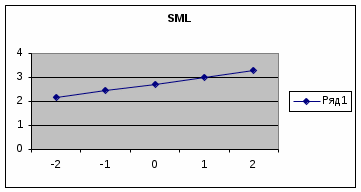  На графике SML по горизонтальной оси отложены коэффициенты  , по вертикальной – эффективность бумаг или портфелей. Прямая SML отражает идеальную зависимость и эффективностью бумаг и портфелей. Все точки, лежащие на прямой SML, соответствуют «справедливо» оцененным бумагам (портфелям), а те которые лежат выше/ниже этой линии – недооцененными/переоцененным. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||