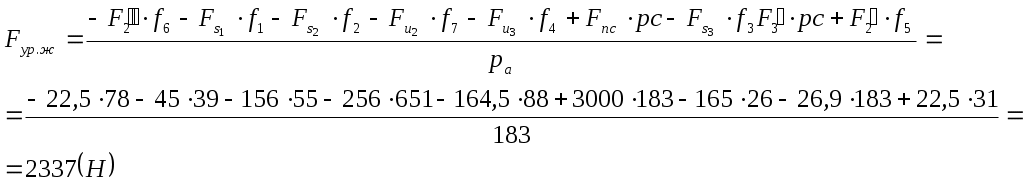|
|
Механика. Контрольная работа по дисциплине прикладная механика направление Технология транспортных процессов
Образовательное учреждение высшего образования
«Южно-Уральский институт управления и экономики»
КОНТРОЛЬНАЯ РАБОТА
ПО ДИСЦИПЛИНЕ Прикладная механика
НАПРАВЛЕНИЕ «Технология транспортных процессов» 23.03.01
Выполнил
студент Шубин А. О.
группа ТТПЗ-301
Проверил
Преподаватель Саврасова Н. Р.
Результат проверки_________________
г. Челябинск, 2019 г.

СОДЕРЖАНИЕ
Техническое задание…………………………………………………
Введение………………………………………………………………
1. Структурный анализ механизма……………………………………..
1.1 Степень подвижности механизма………………………………
1.2 Разбивка механизма на группы Ассура и начальный механизм…
1.3 Формула строения механизма……………………………………..
2. Кинематический анализ механизма…………………………………..
2.1 Построение 12 положений плана механизма…………………….
2.2 Построение плана скоростей……………………………………..
2.3 Построение плана ускорений…………………………………….
3. Силовой анализ механизма…………………………………………..
3.1 План механизма в заданном положении………………………..
3.2 Механическая характеристика сил полезного сопротивления…
3.3 Определение реакций в кинематических парах…………………
Заключение…………………………………………………………….
Список использованной литературы…………………………………

ТЕХНИЧЕСКОЕ ЗАДАНИЕ
Механизм бревносбрасывателя
Параметры расчета:
Длина кривошипа 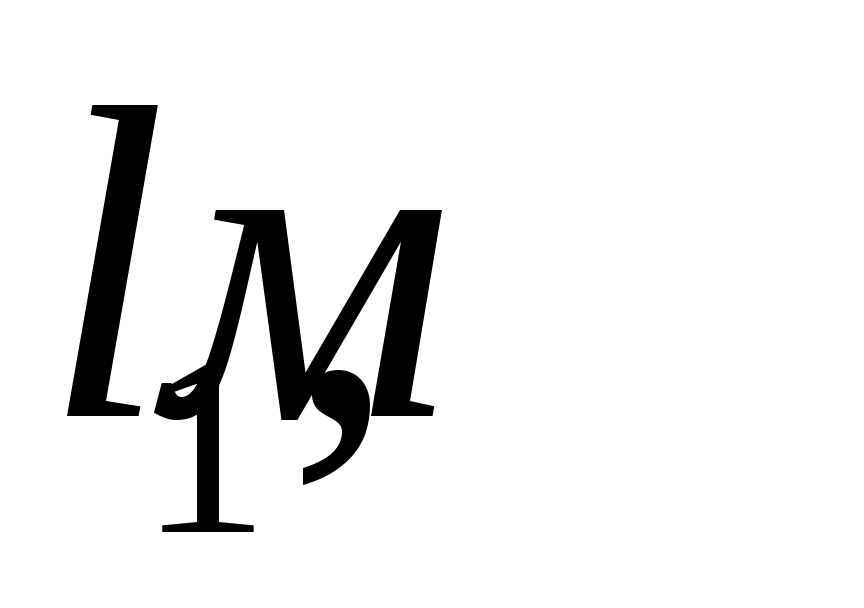
|
0,25
|
Длина шатуна 
|
0,6
|
Длина коромысла 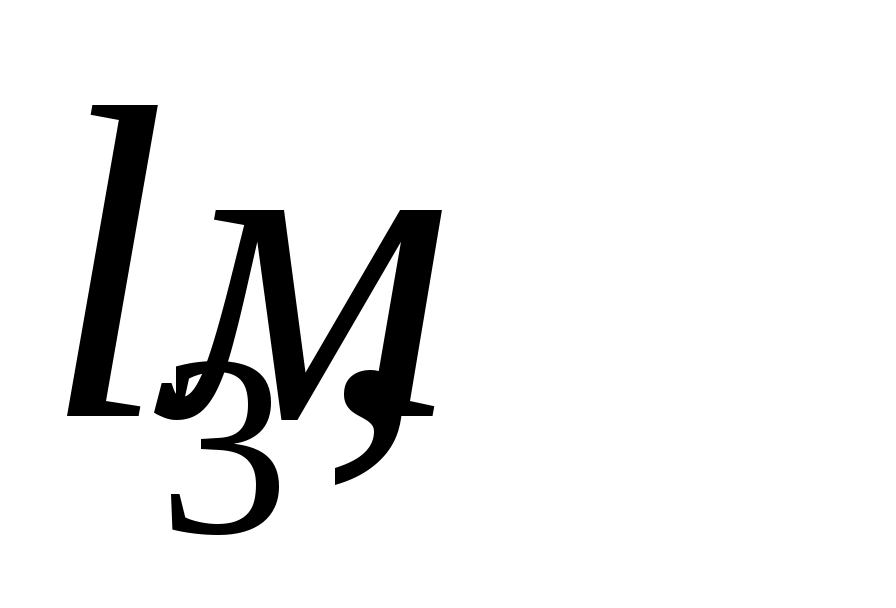
|
0,72
|
Расстояние 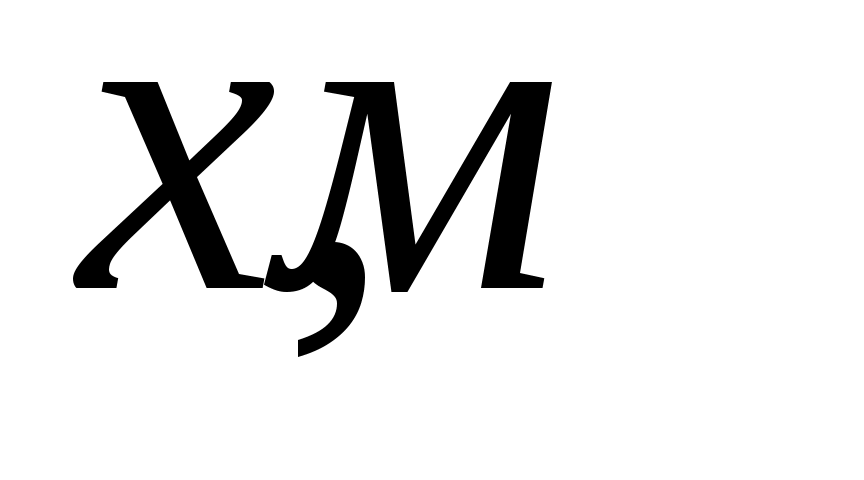
|
0,56
|
Масса кривошипа 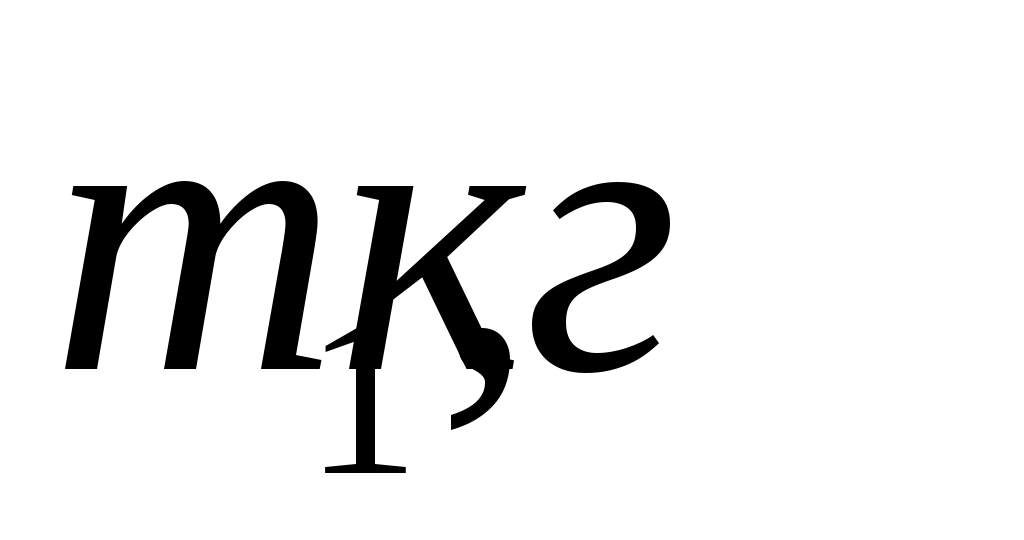
|
7
|
Масса шатуна 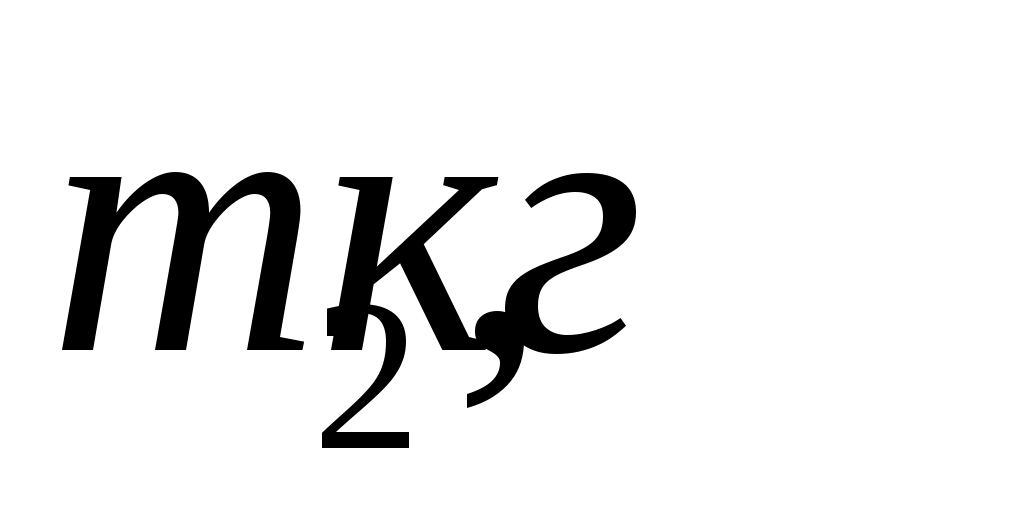
|
18
|
Масса коромысла 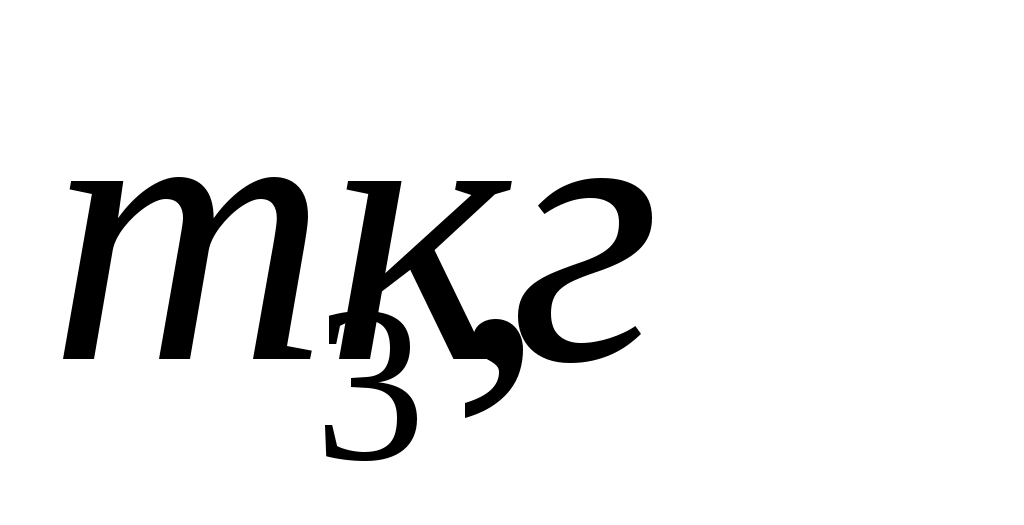
|
21
|
Радиус инерции шатуна 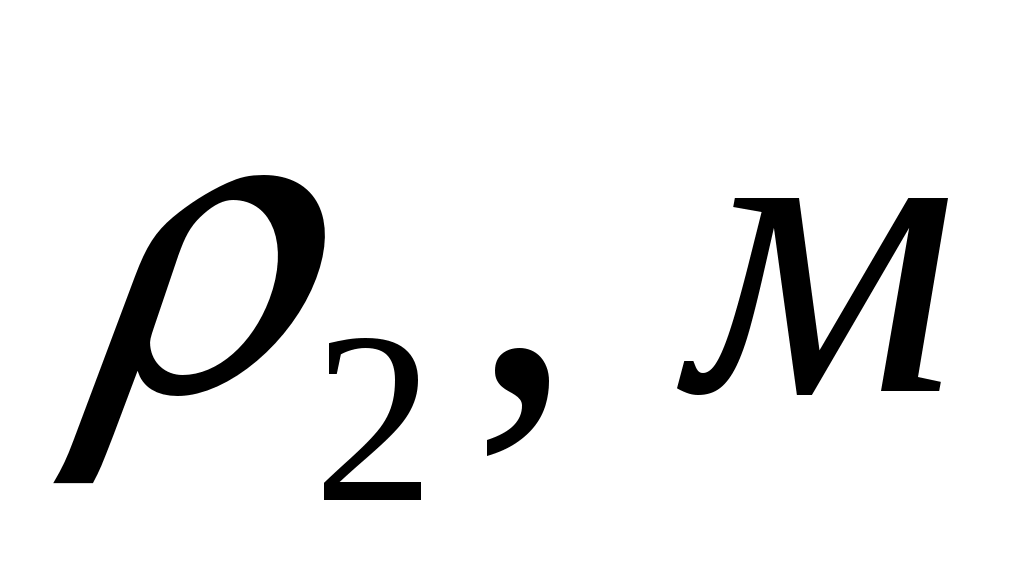
|
0,115
|
Максимальный момент силы полезного сопротивления 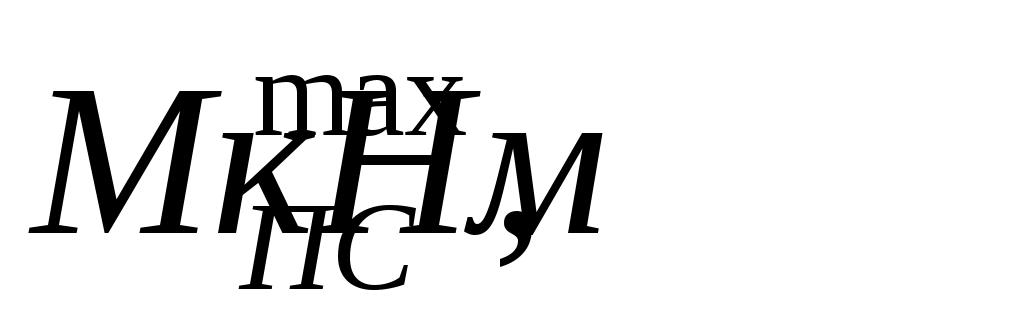
|
0,67
|
Относительная ширина маховика 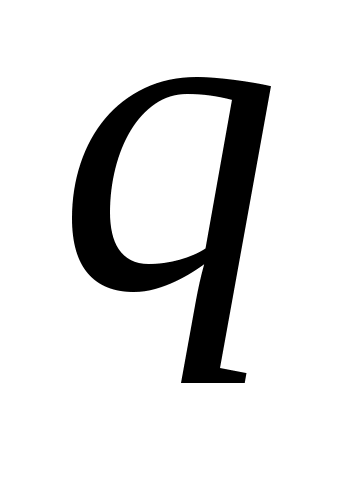
|
0,15
|
Материал маховика
|
чугун
|
Угловая скорость кривошипа 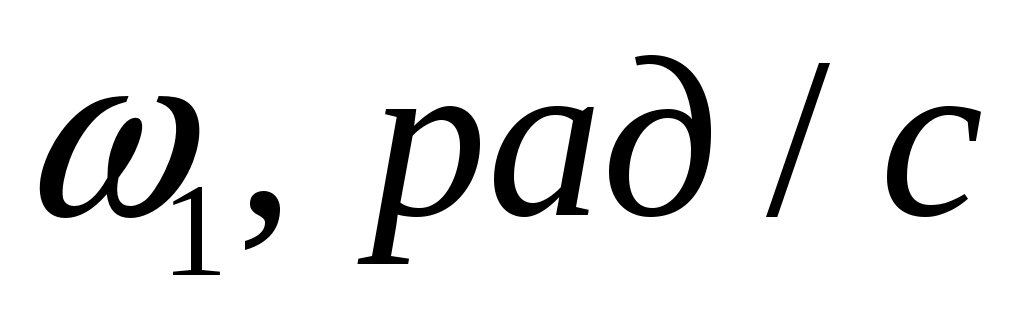
|
30
|
Угол поворота кривошипа в расчетном положении, град
|
60
|
Расчетная схема:
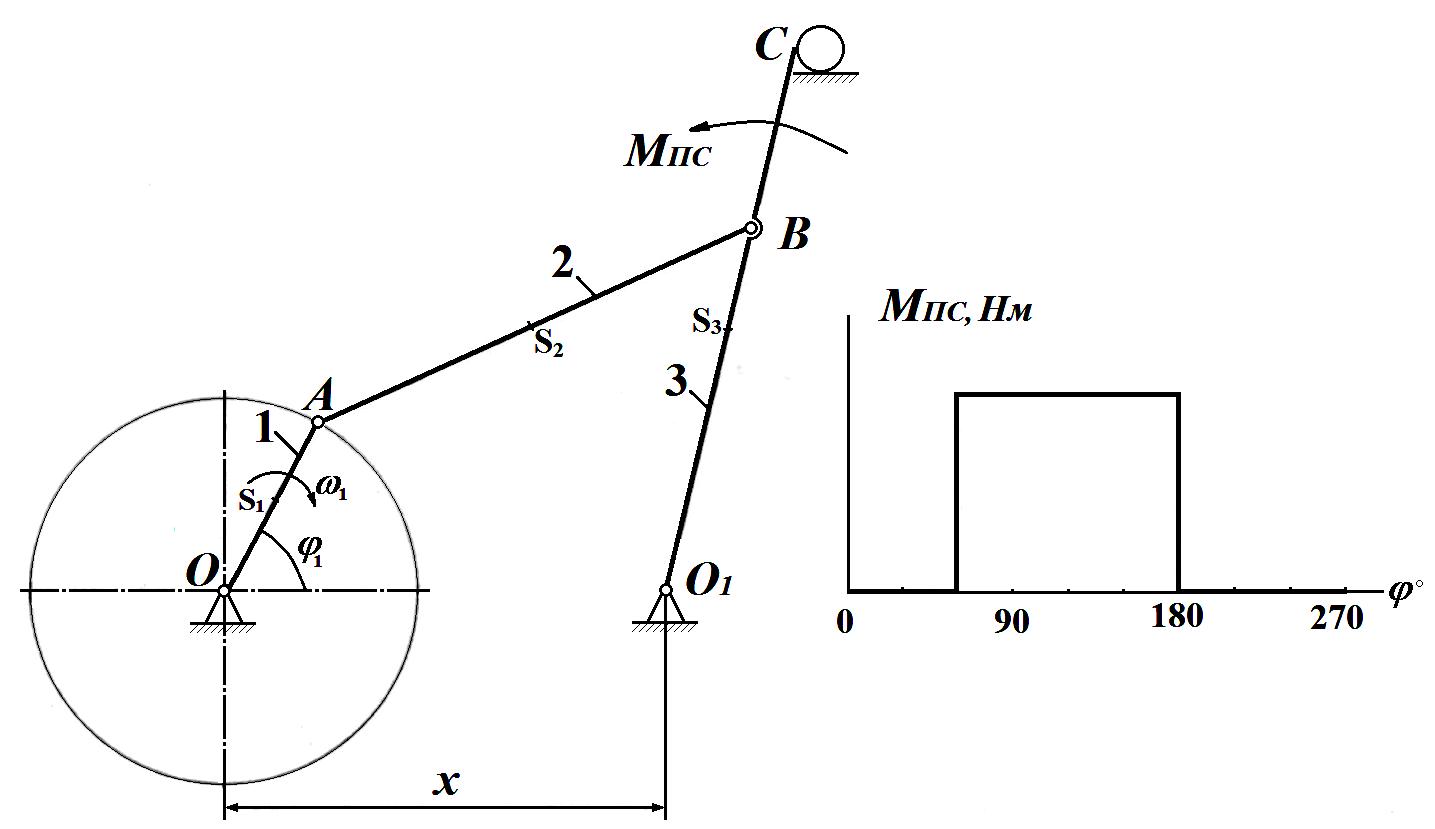
Рис. 1 Структурная схема плоского механизма
 Введение Введение
Основой целью выполнения задания является изучение общих методов исследования и проектирования механизмов; применение знаний из ранее изученных дисциплин для конструирования, изготовления и эксплуатации машин в любой отрасли промышленности и транспорта.
Задачей данной работы является проведение структурного, кинематического и силового анализа механизма, методами построения планов скоростей, ускорений и сил.
При выполнении графической части проекта использованы результаты проведенных расчетов.
Поставленные задачи решались с учетом действующих стандартов предприятия и рекомендациях, учитывающих опыт создания подобных устройств.
 1. Структурный анализ механизма 1. Структурный анализ механизма
1.1 Степень подвижности механизма
Проведём структурный анализ для кривошипно-коромыслового механизма. Структурная схема механизма в соответствии с принятыми условными обозначениями изображает звенья механизма, их взаимное расположение, а также подвижные пары между звеньями. На схеме звенья обозначены цифрами, кинематические пары - заглавными латинскими буквами.
Заданный механизм представляет собой кривошипно-шатунный механизм, состоящий из трех подвижных звеньев:
- 1 кривошип,
- 2 шатун,
- 3 коромысло.
Звенья связаны между собой и со стойкой четырьмя кинематическими парами О, А, В, О1. Все кинематические пары вращательные, одноподвижные 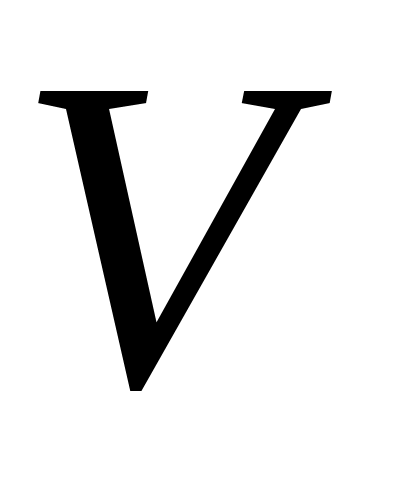 класса. класса.
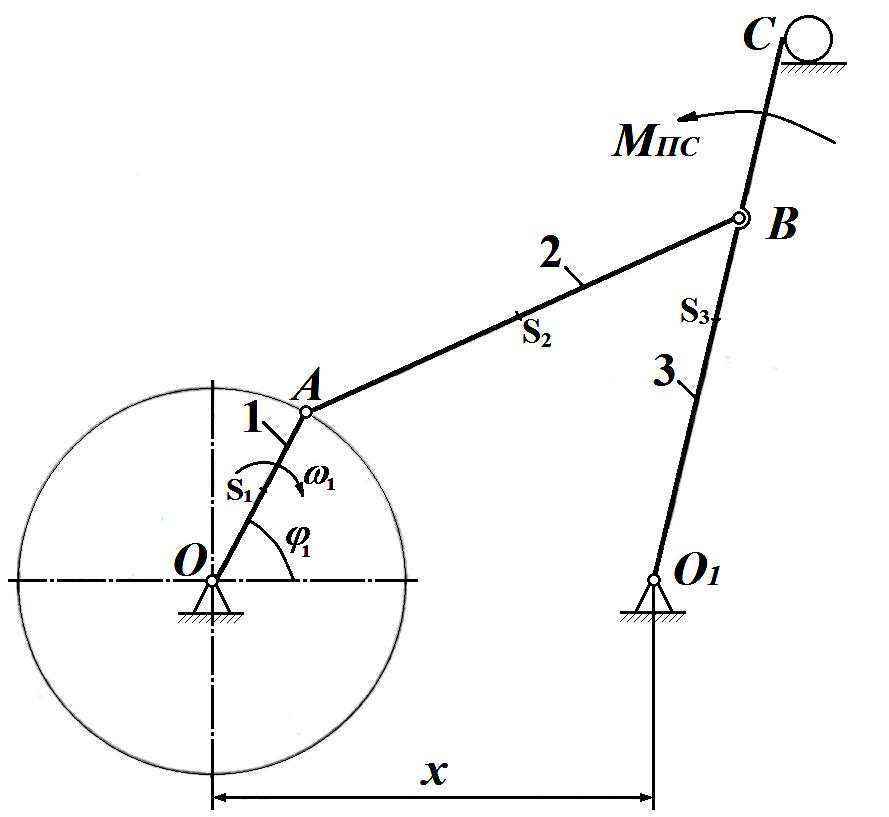
Рис 2. Структурная схема механизма

В нашем случае механизм плоский (траектории всех точек в параллельных плоскостях). Поэтому степень подвижности находим по формуле Чебышева:
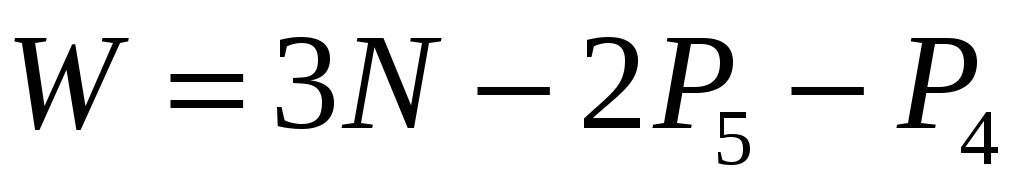
где 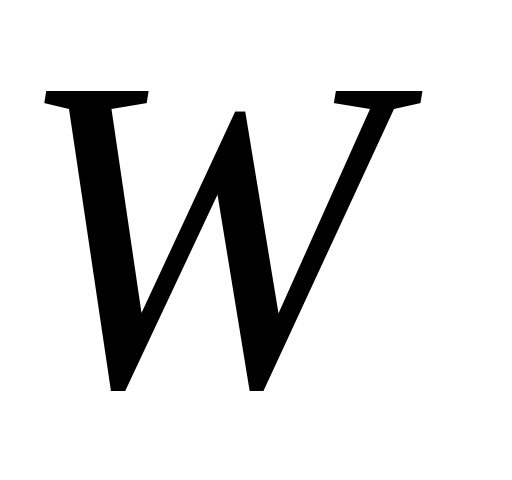 - число степеней свободы; - число степеней свободы;
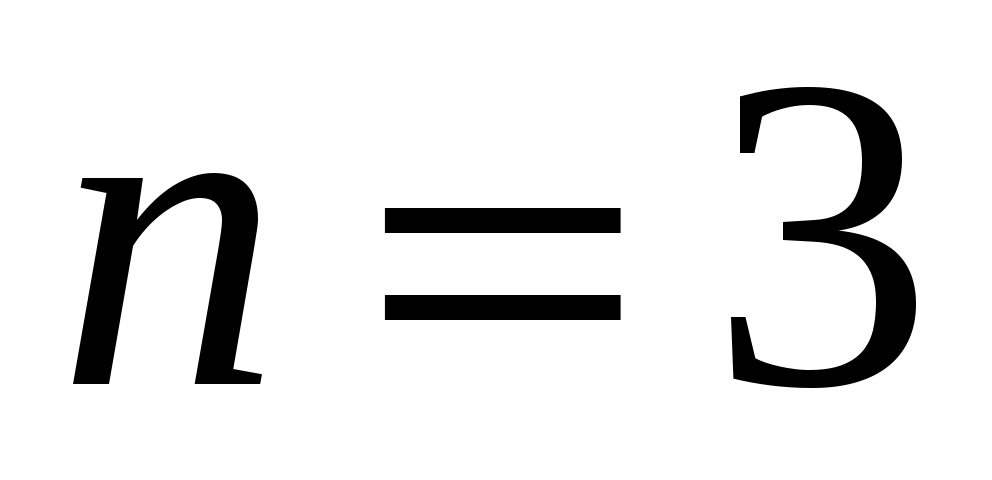 - количество подвижных звеньев: 1, 2, 3; - количество подвижных звеньев: 1, 2, 3;
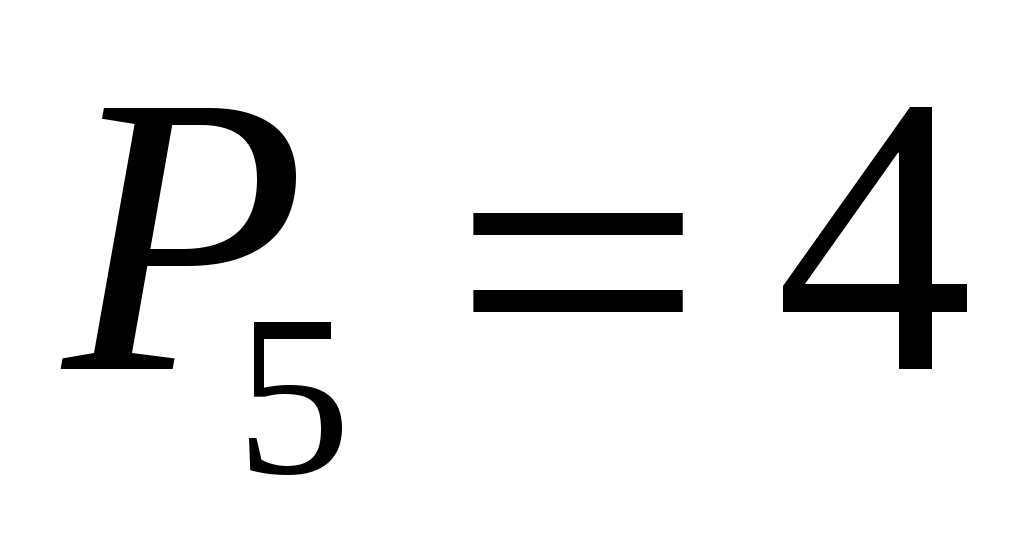 - число кинематических пар Vкласса: О, А, В, О1 (вращательные); - число кинематических пар Vкласса: О, А, В, О1 (вращательные);
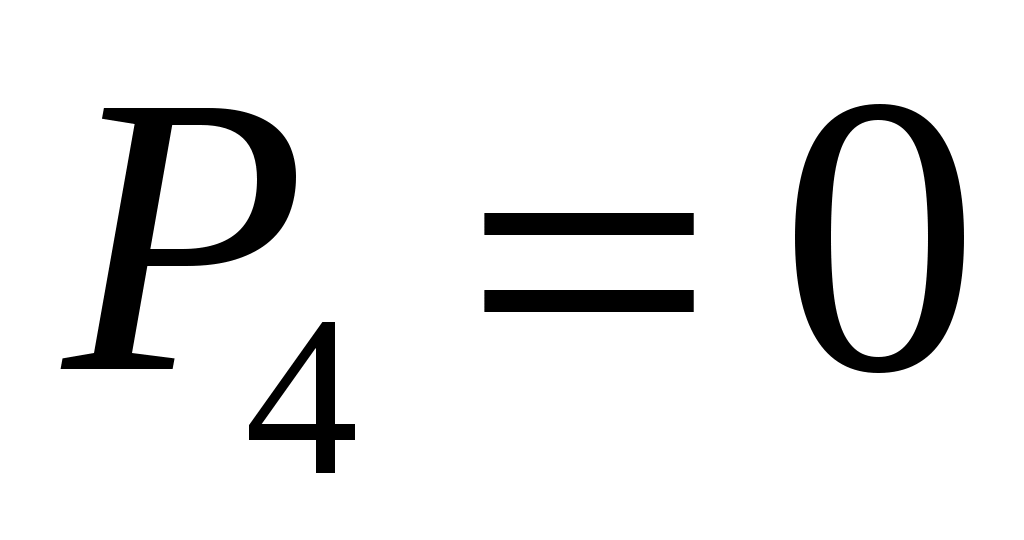 - число кинематических пар IV класса. - число кинематических пар IV класса.
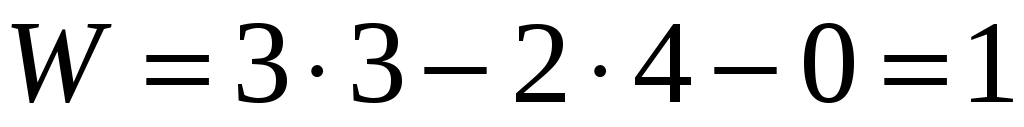 . .
1.2 Разбивка механизма на группы Ассура и начальный механизм
Механизм состоит из одной группы Ассура 3-2 и начального механизма ОА.
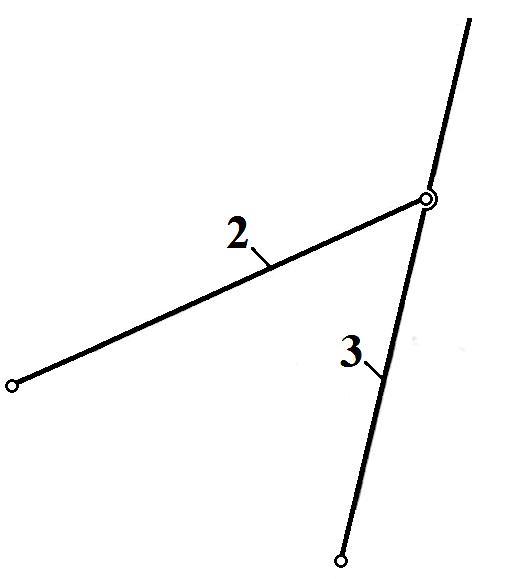
Рис. 3 Группа Ассура II класса, двухповодковая.
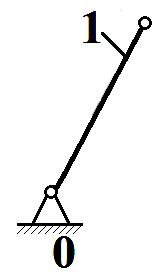
Рис. 4 Начальный механизм 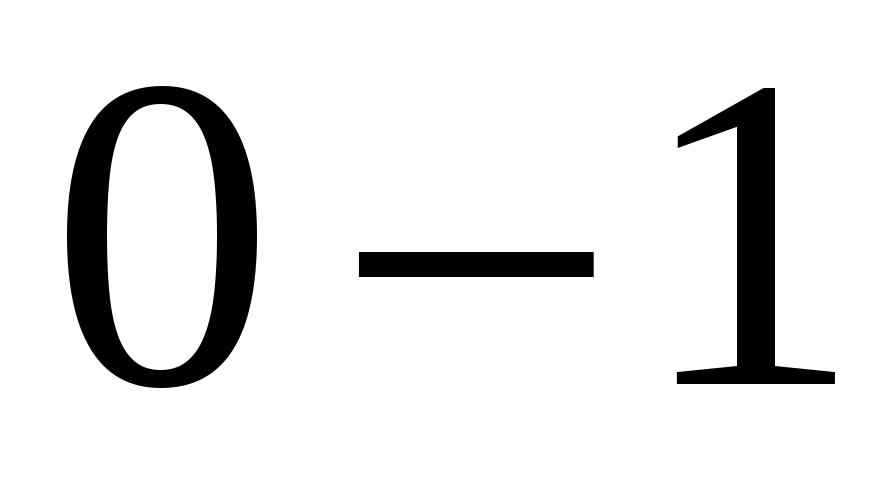
1.3 Формула строения механизма
Механизм второго класса (по max II классу группы Ассура).
Структурная формула механизма: 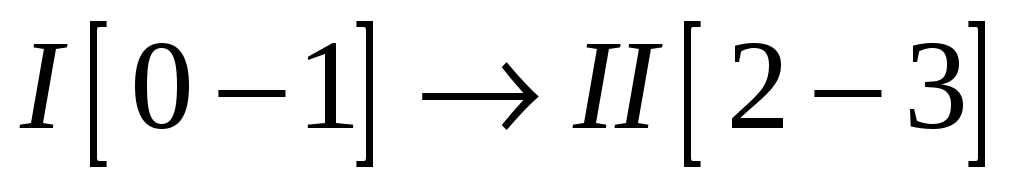 . .

2. Кинематический анализ механизма
Данные для расчета:
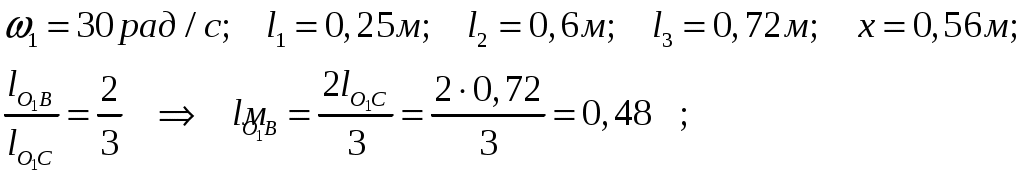
2.1 Построение 12 положений звеньев механизма.
При построении кинематических схем и планов положений механизмов определяется масштаб длины, 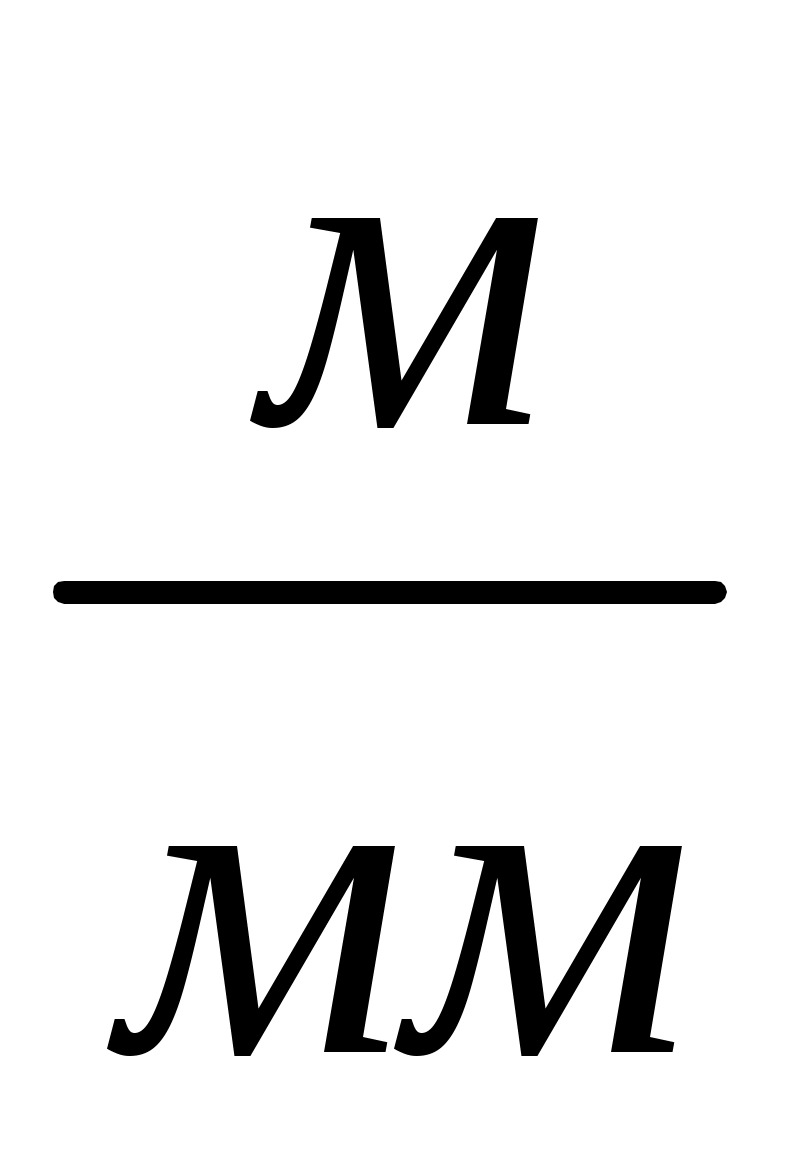 : :
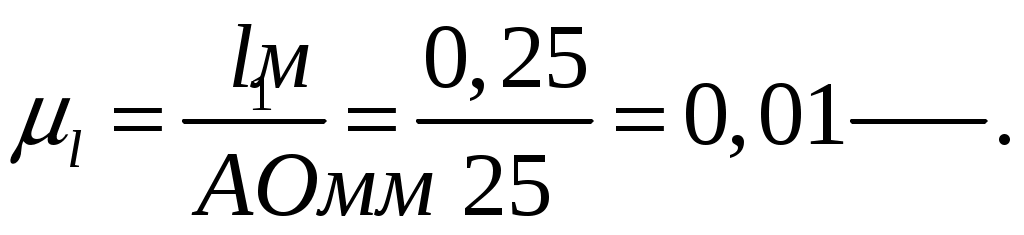
где: 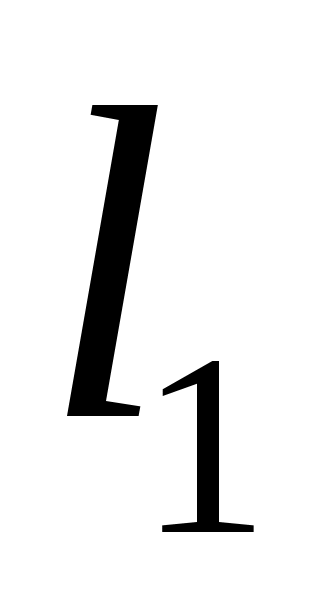 - действительная длина кривошипа, - действительная длина кривошипа,  ; ;
 - длина отрезка на плане механизма, изображающего кривошип, - длина отрезка на плане механизма, изображающего кривошип, . .
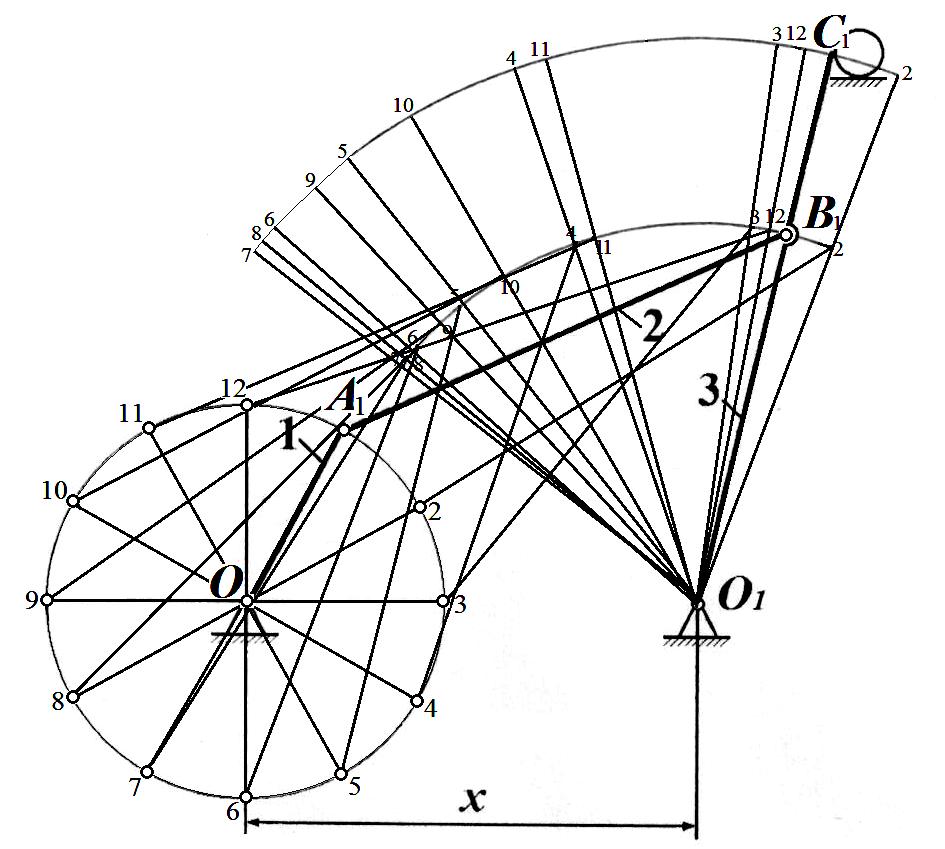
Рис. 5 Построение 12 положений звеньев механизма

2.2 Построение плана скоростей
Строим в масштабе план кинематической схемы механизма при заданном угле поворота кривошипа 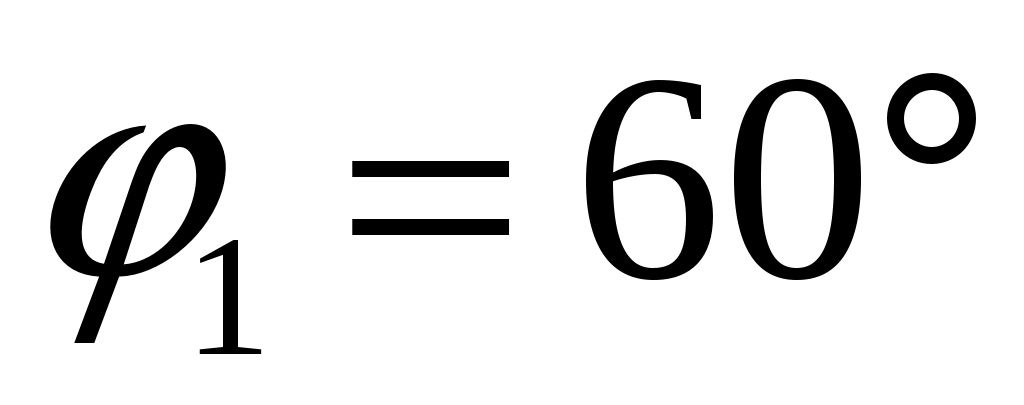 . .
План механизма 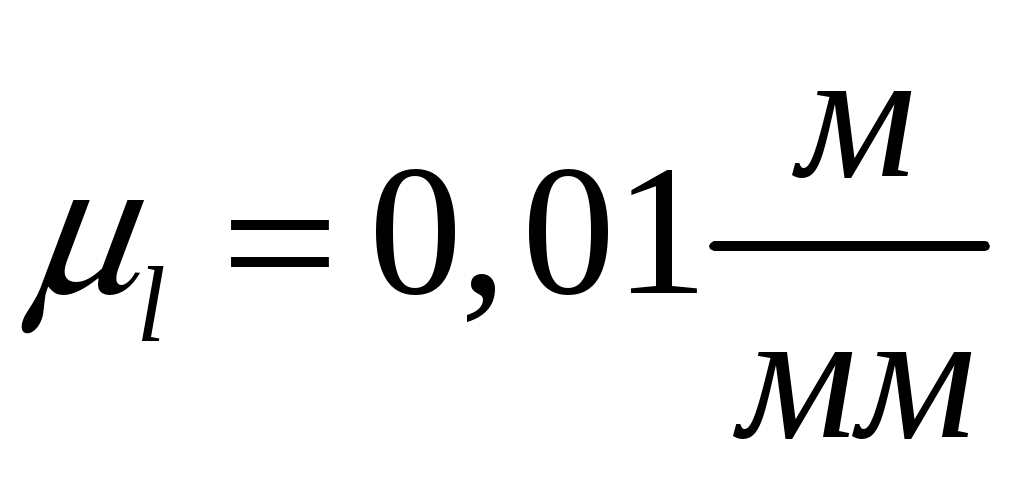
- Скорость точки А.
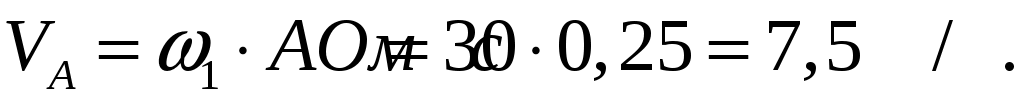
Из произвольной точки Р, принятой за полюс плана скоростей строим отрезок 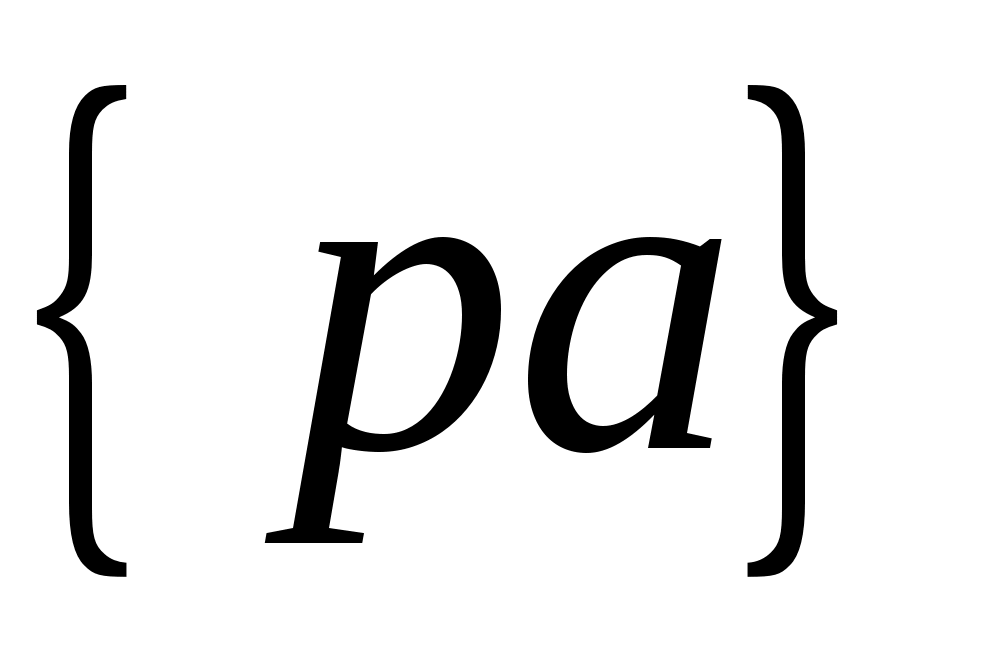 , соответствующий вектору , соответствующий вектору 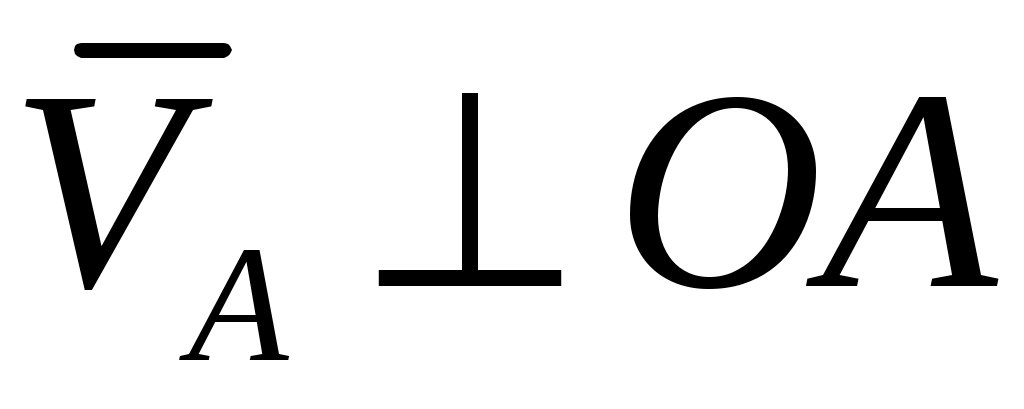 длиной 100 мм, тогда масштабный коэффициент плана скоростей равен: длиной 100 мм, тогда масштабный коэффициент плана скоростей равен:
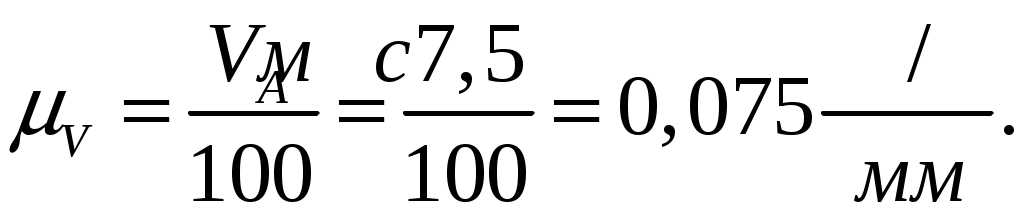
- Скорость точки В
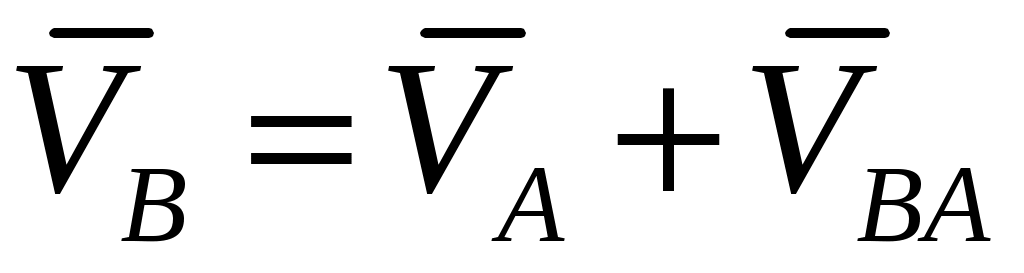
Из полюса проводим линию, перпендикулярную 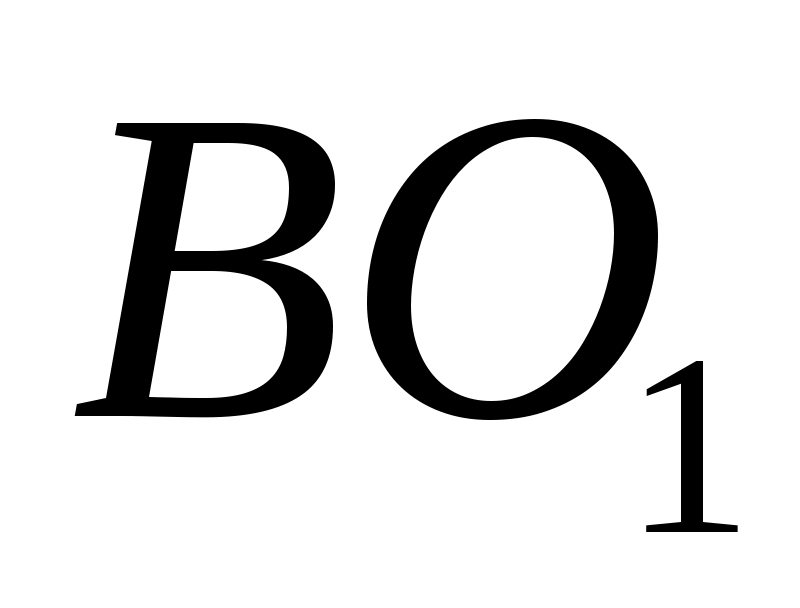 , а из конца отрезка , а из конца отрезка 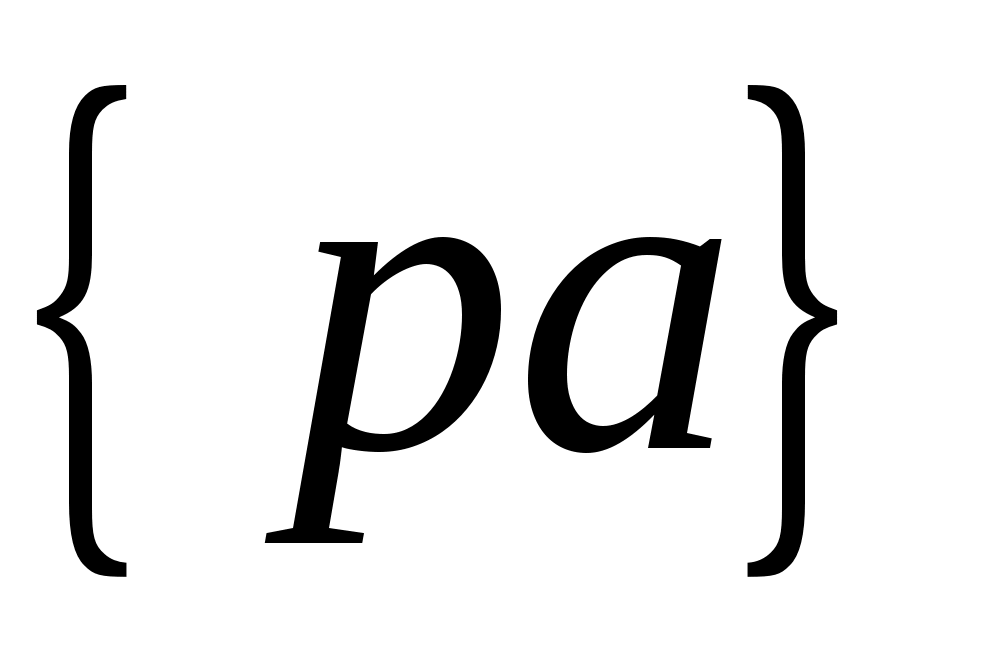 - линию, перпендикулярную - линию, перпендикулярную 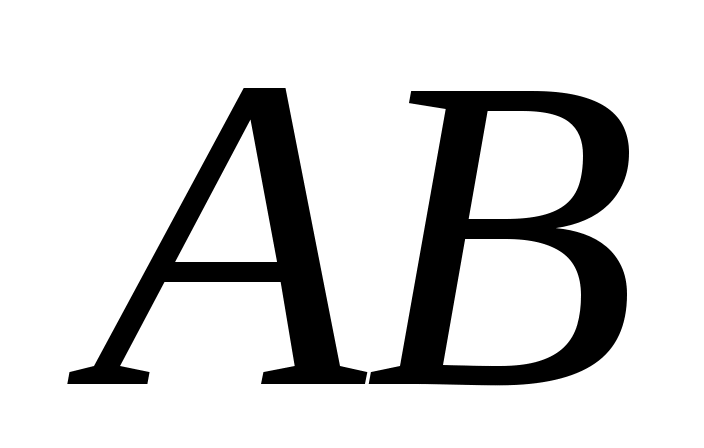 . Пересечение этих линий дает на плане скоростей точку . Пересечение этих линий дает на плане скоростей точку 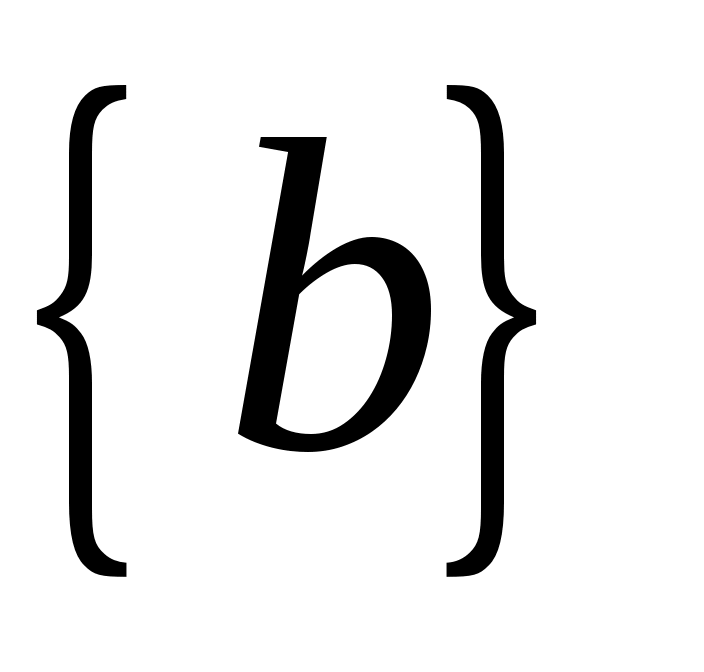 , причем отрезок , причем отрезок 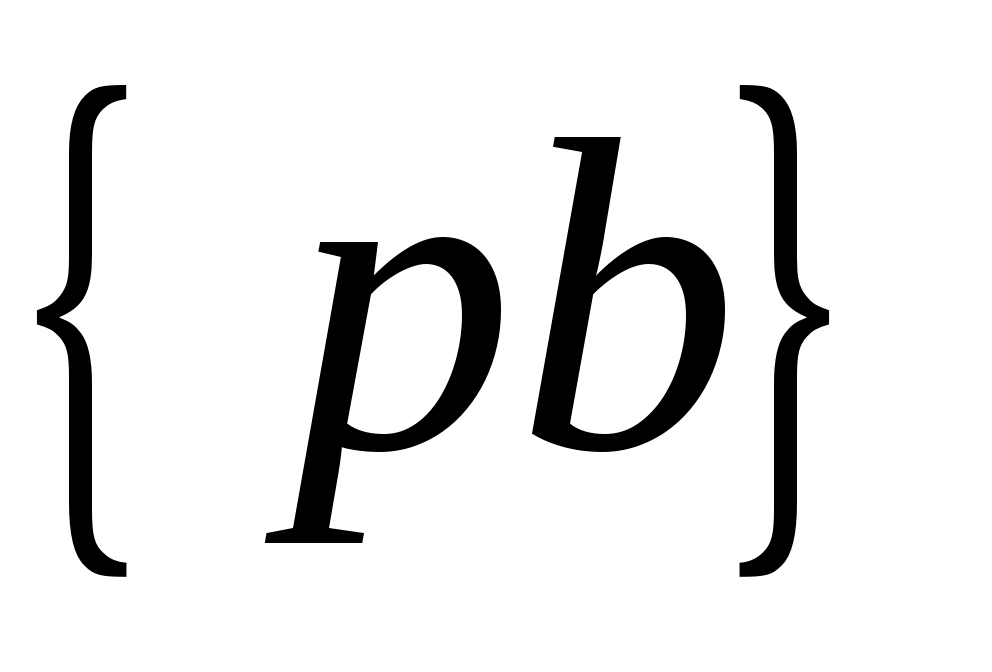 изображает скорость точки изображает скорость точки 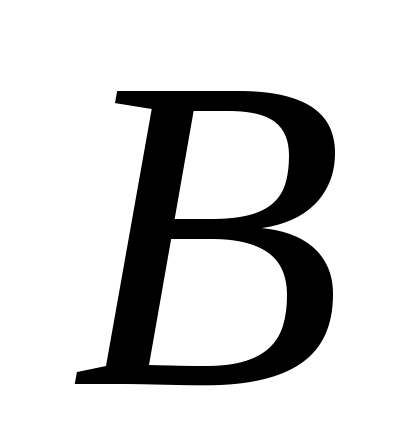 , а отрезок , а отрезок 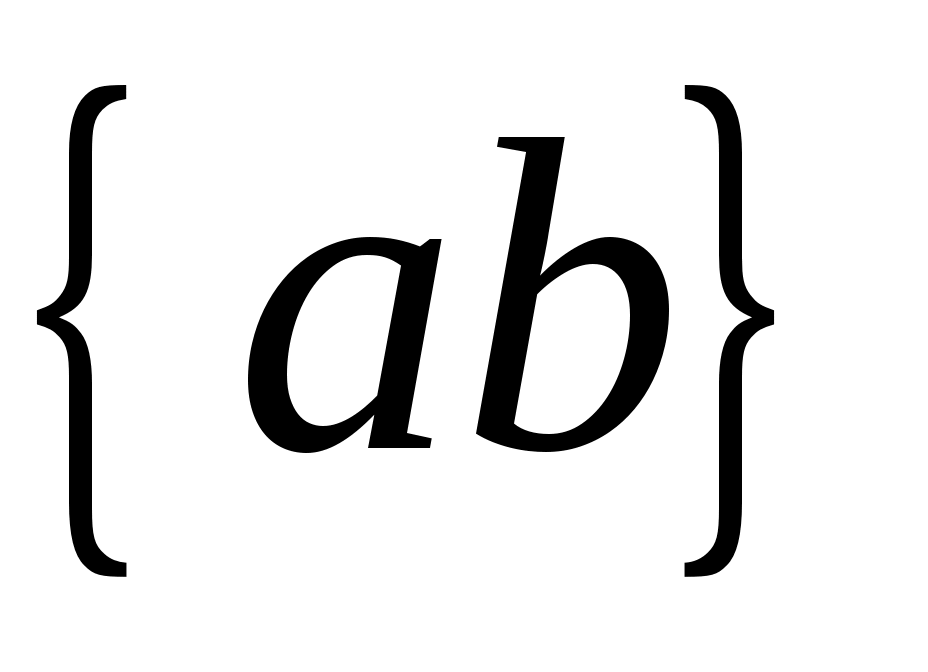 - скорость точки - скорость точки  относительно точки относительно точки  Численные значения скоростей: Численные значения скоростей:
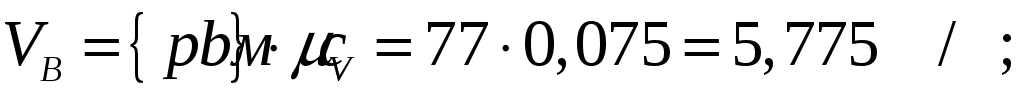
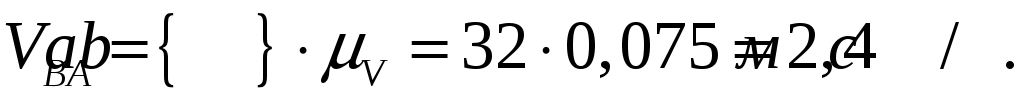
Для определения скорости точки  воспользуемся принципом подобия плана скоростей и плана механизма, согласно которому точки звена расположены подобно соответствующим точкам плана. Поскольку в механизме точка В находится на 2/3 звена воспользуемся принципом подобия плана скоростей и плана механизма, согласно которому точки звена расположены подобно соответствующим точкам плана. Поскольку в механизме точка В находится на 2/3 звена 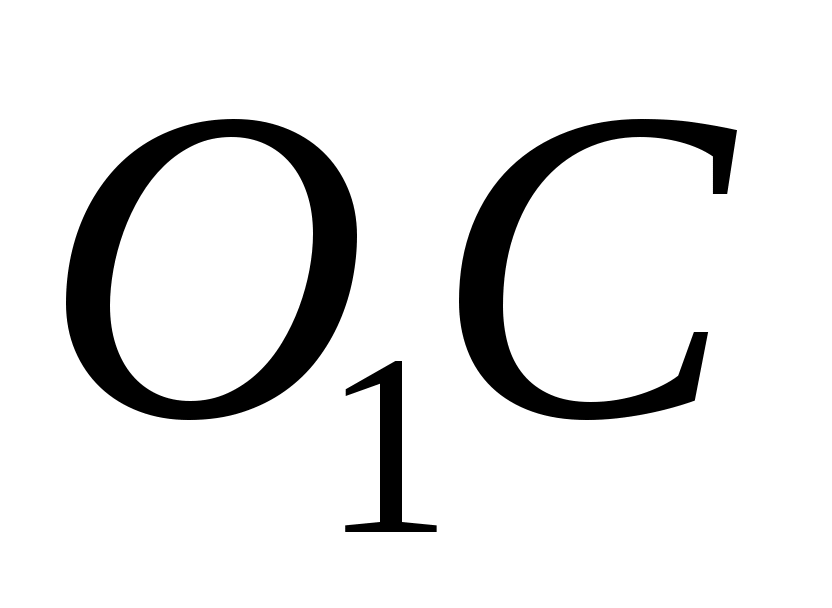 , то и на плане скоростей , то и на плане скоростей 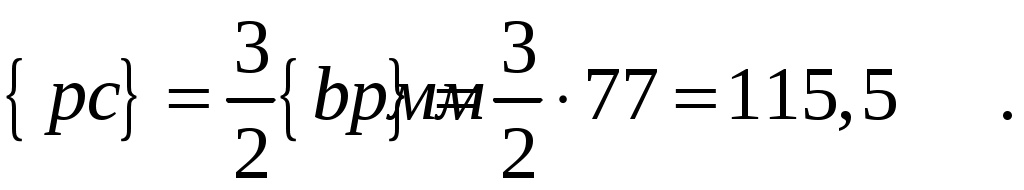
Численные значения скорости точки С:
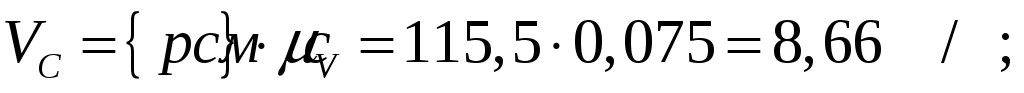

Используя принцип подобия строим на плане скорости центров масс звеньев. Центры масс расположены на серединах звеньев, значит и на плане скоростей они будут расположены на серединах отрезков, соответствующих звеньям.
Численные значения скоростей центров масс:
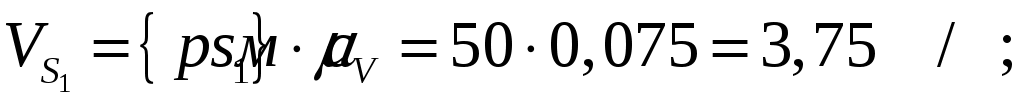
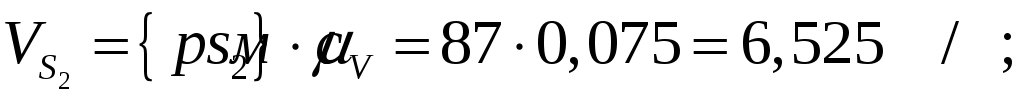
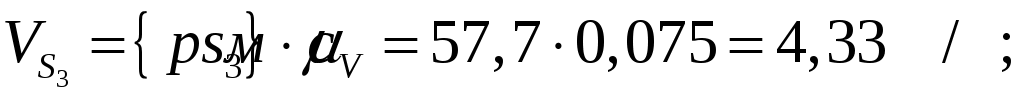
Угловые скорости звеньев:
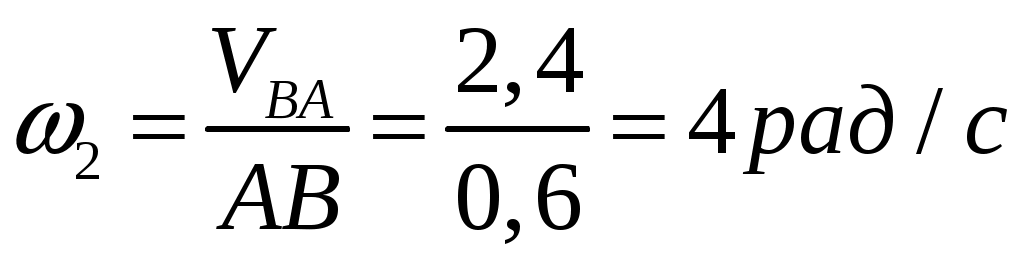 ; ;
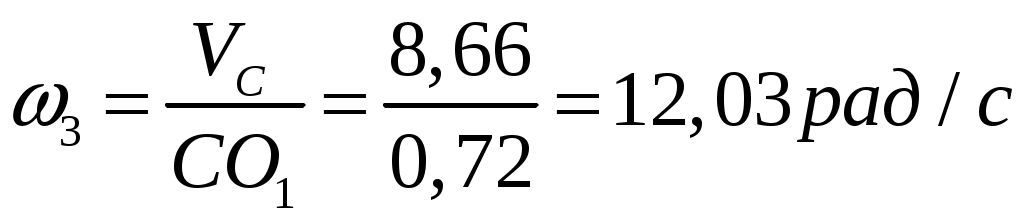 ; ;
2.3 Построение плана ускорений
Определить методом планов ускорения всех подвижных шарниров и угловые ускорения звеньев.
Ускорение точки 
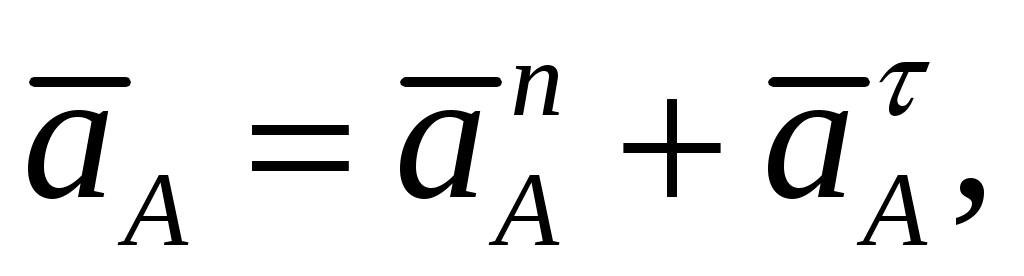
где 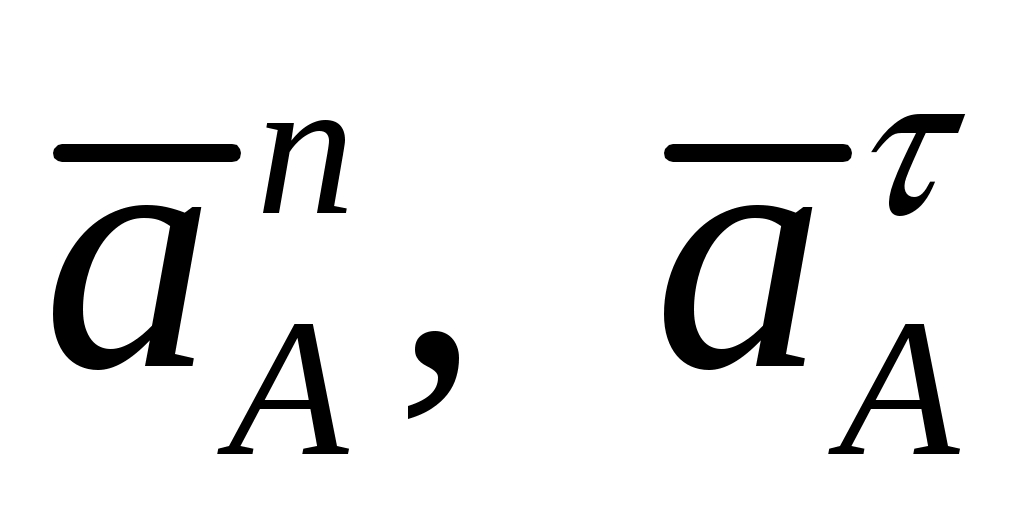 - нормальная и тангенциальная составляющие. - нормальная и тангенциальная составляющие.
Поскольку угловая скорость 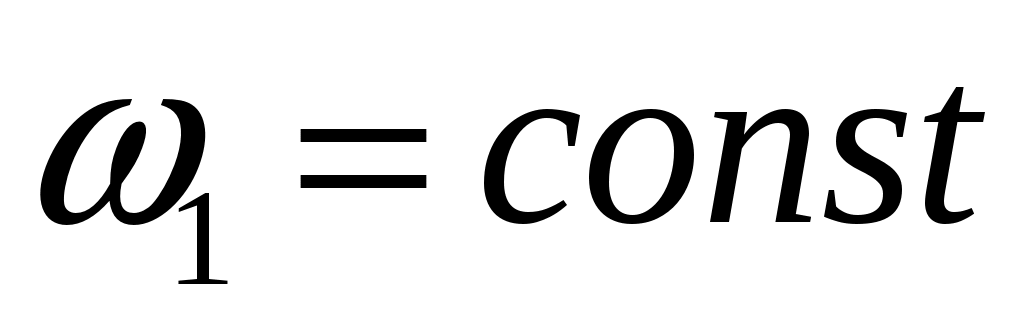 угловое ускорение угловое ускорение 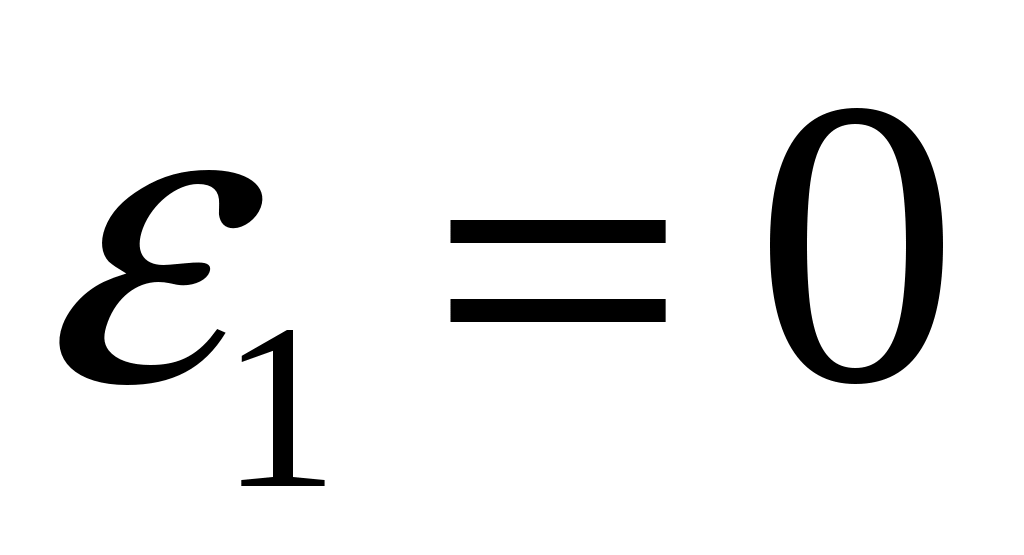 и и 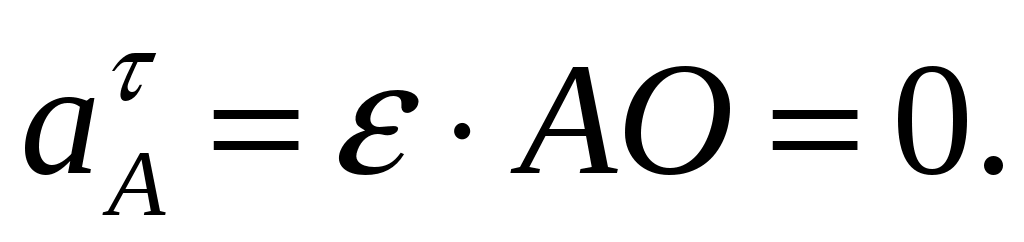 Тогда Тогда
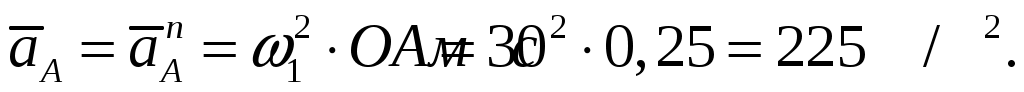
Из произвольной точки  - полюса плана ускорений откладываем отрезок - полюса плана ускорений откладываем отрезок 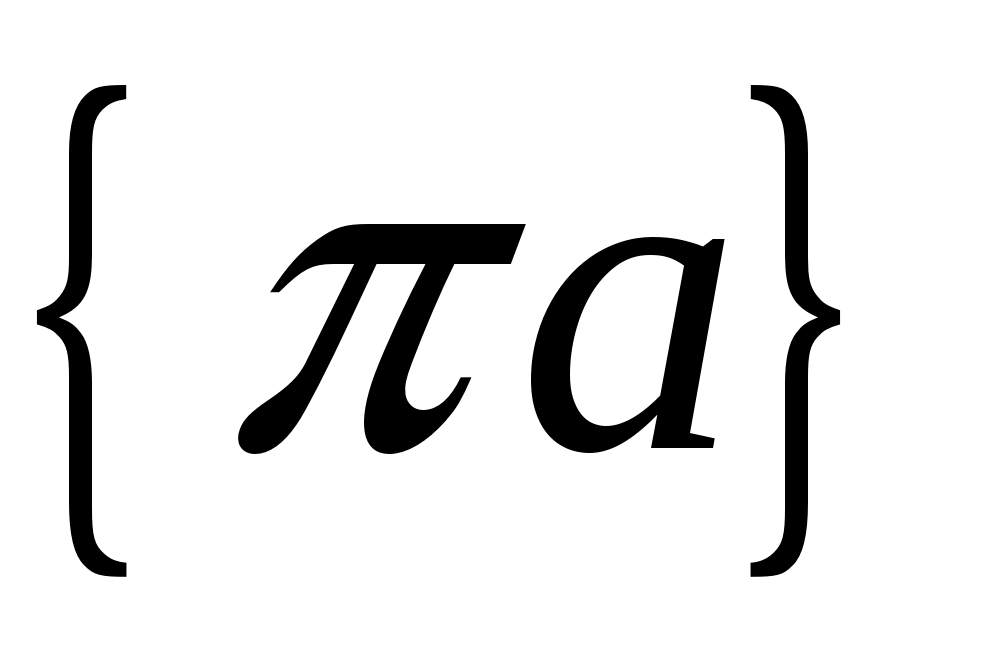 длиной длиной 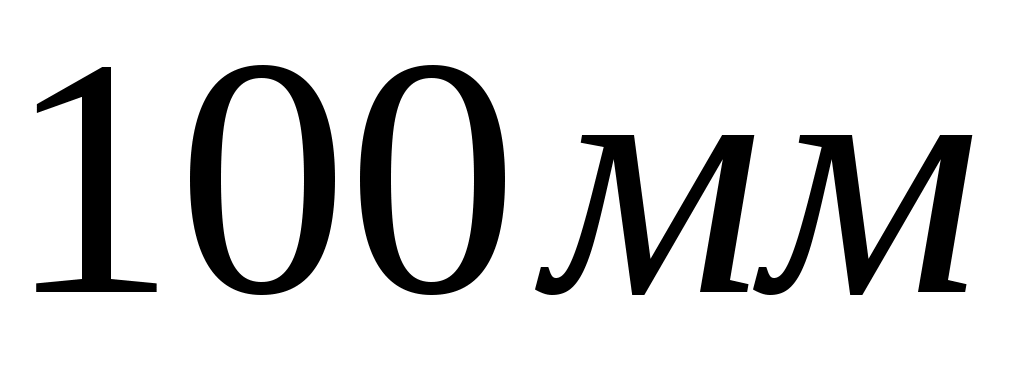 , направленный параллельно звену , направленный параллельно звену 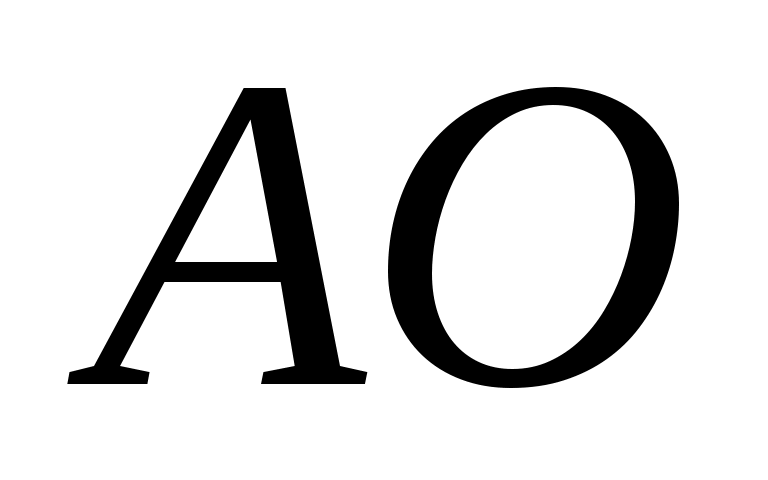 в сторону точки в сторону точки 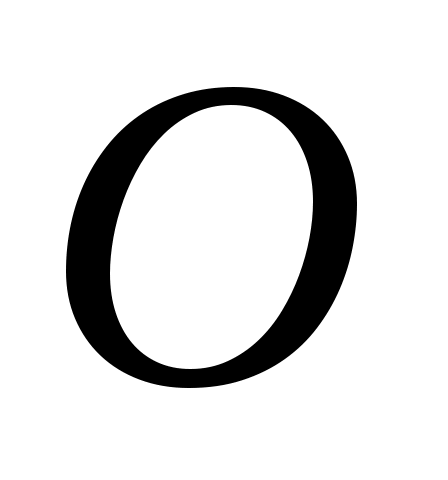 , как и вектор нормальной составляющей , как и вектор нормальной составляющей 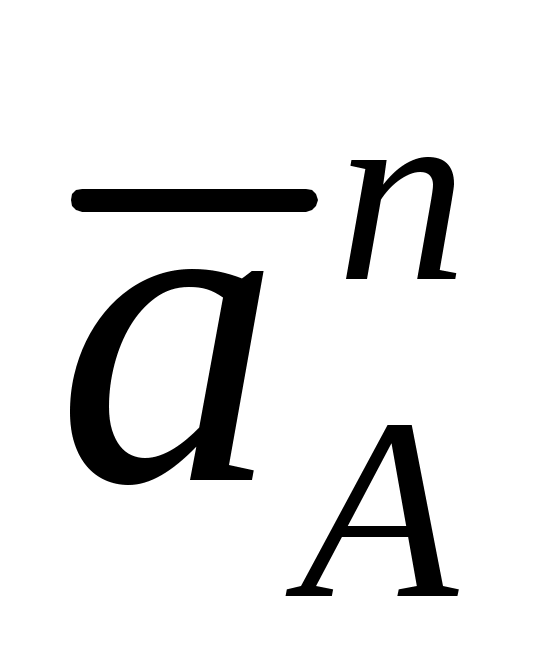 . .
Масштабный коэффициент плана ускорений:
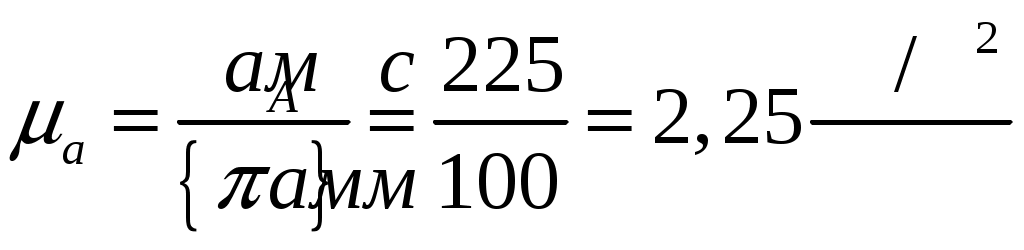 . .
План ускорений
 Ускорение точки Ускорение точки 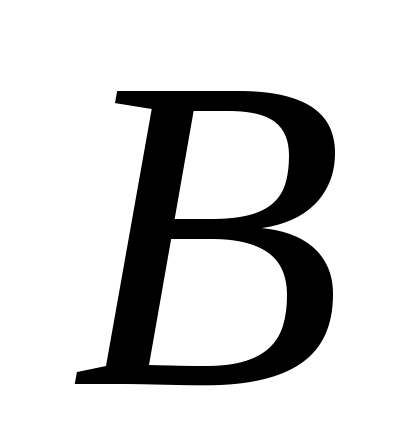 находим по принципу относительности движения, рассматривая два уравнения: находим по принципу относительности движения, рассматривая два уравнения:
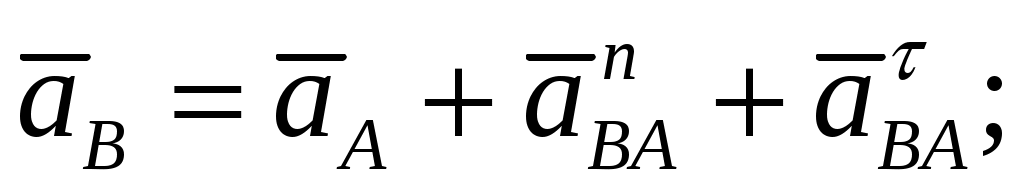
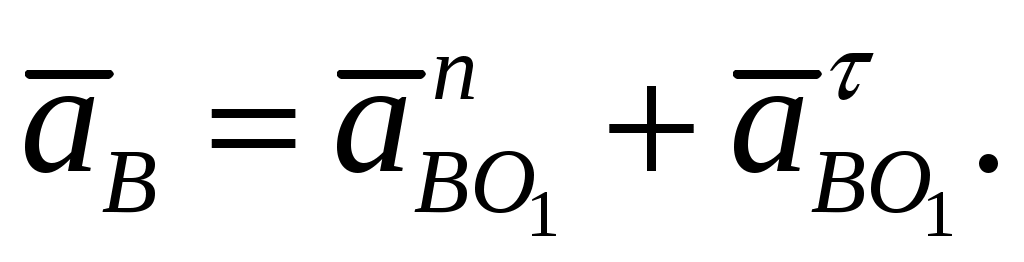
Приравниваем правые части уравнений
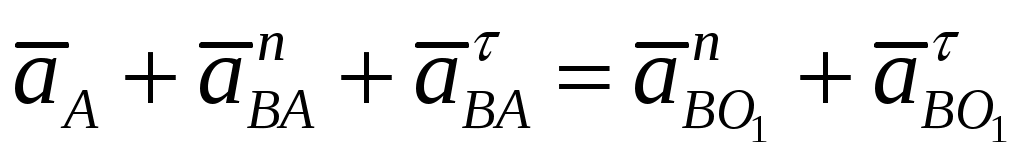
Направления нормальных составляющих 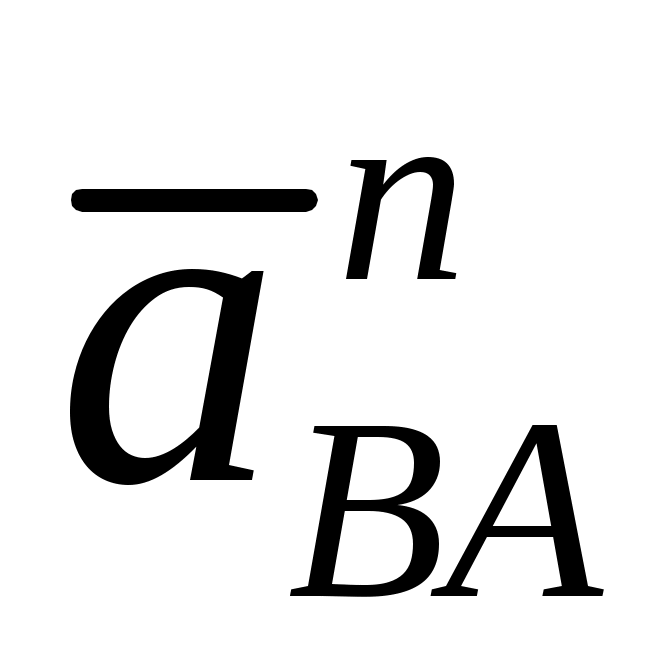 и и 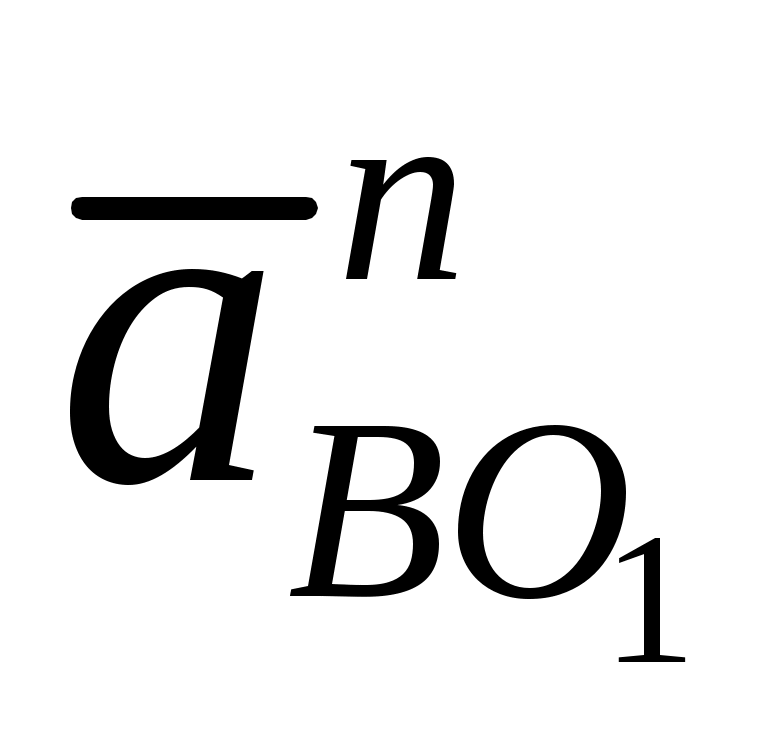 параллельны звеньям параллельны звеньям 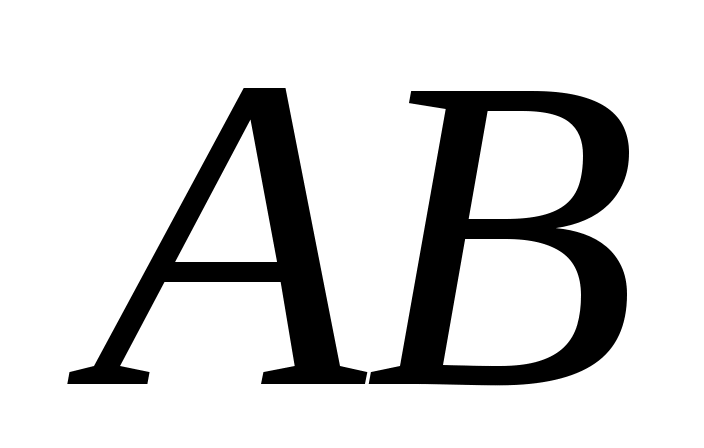 и и 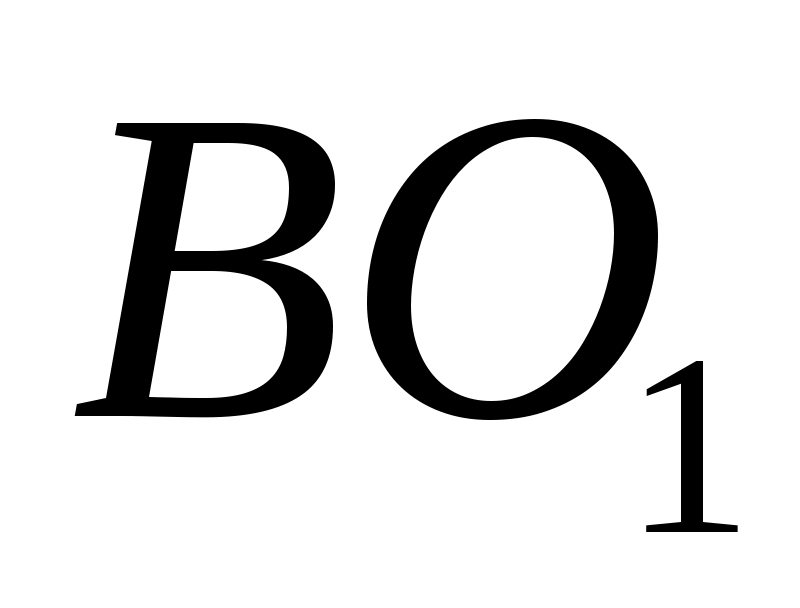 соответственно и направлены к центрам вращения. Их численные значения равны: соответственно и направлены к центрам вращения. Их численные значения равны:
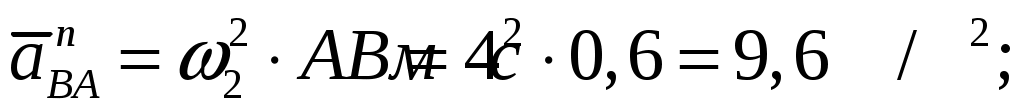
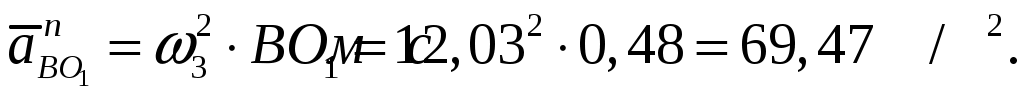
Направления тангенциальных составляющих перпендикулярны этим звеньям, их численные значения неизвестны.
На плане ускорений длины отрезков 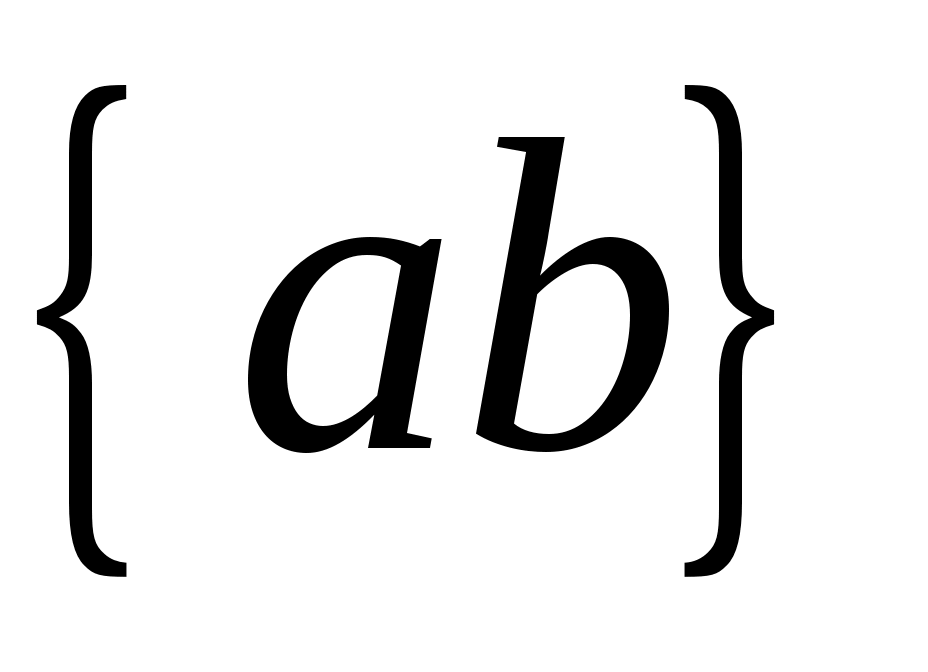 и и 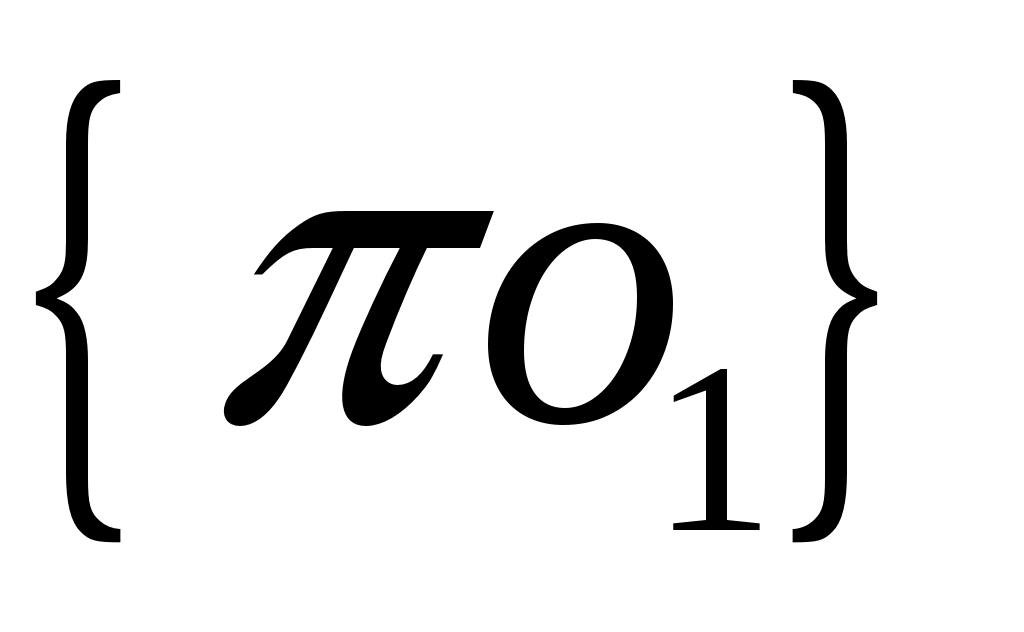 , соответствующих ускорениям , соответствующих ускорениям 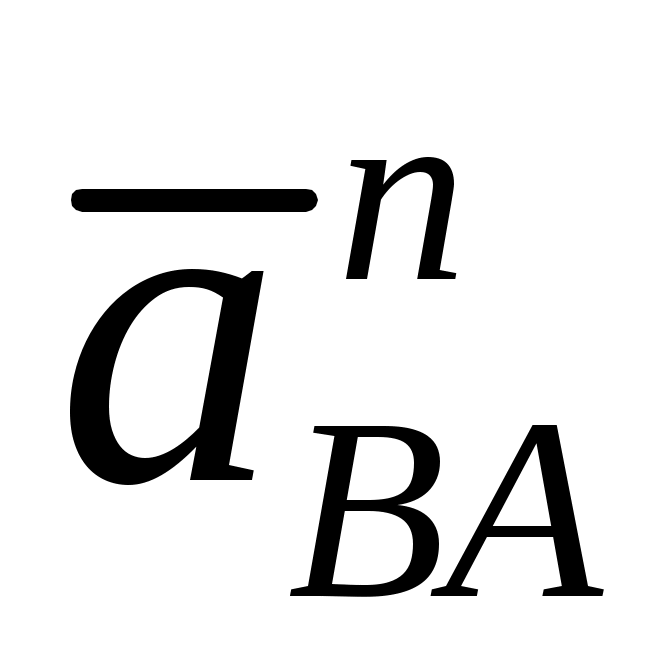 и и 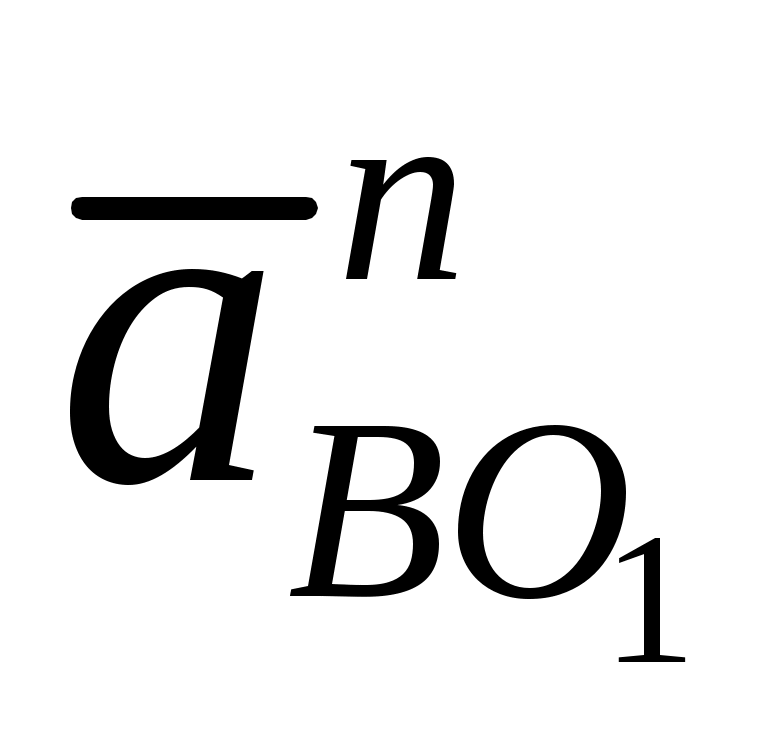 равны: равны:
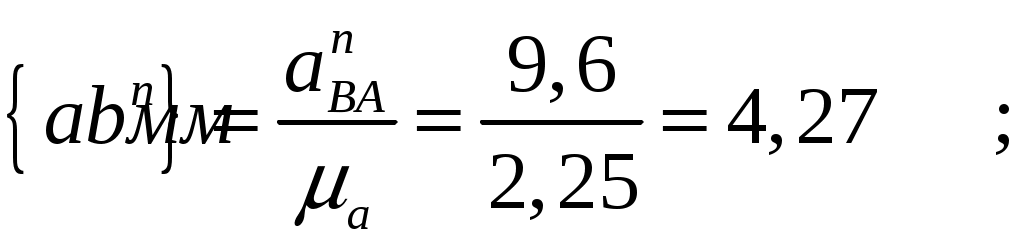
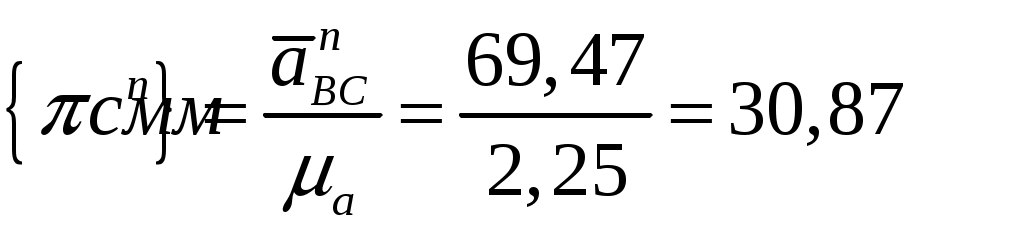 . .
Откладываем из точки  отрезок отрезок 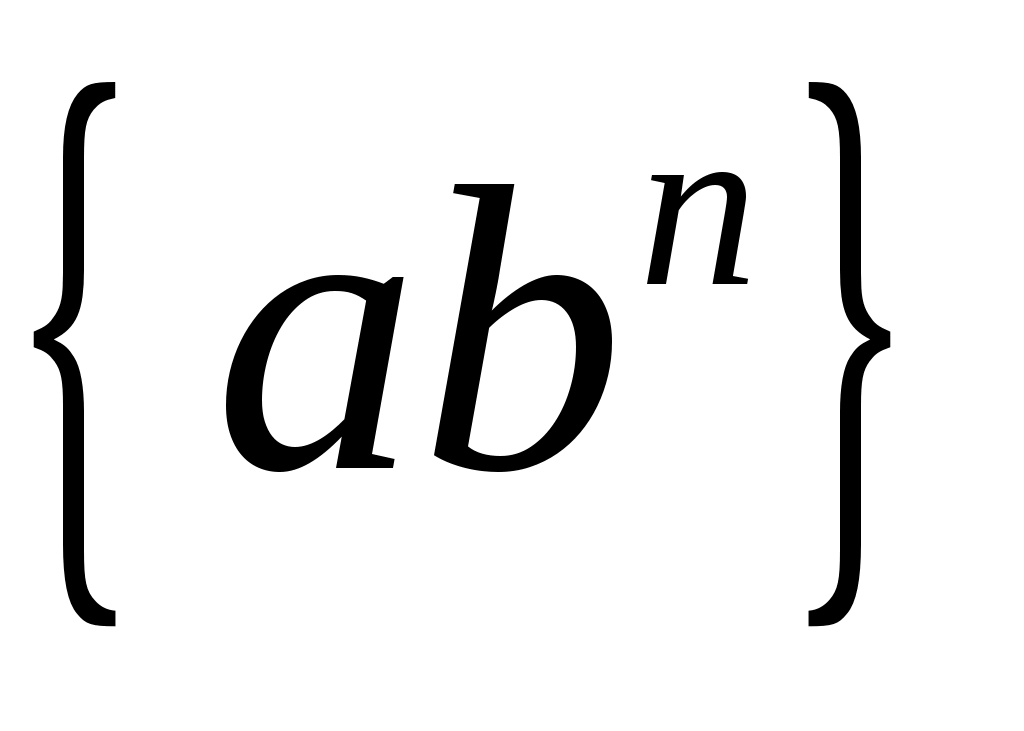 и из точки и из точки 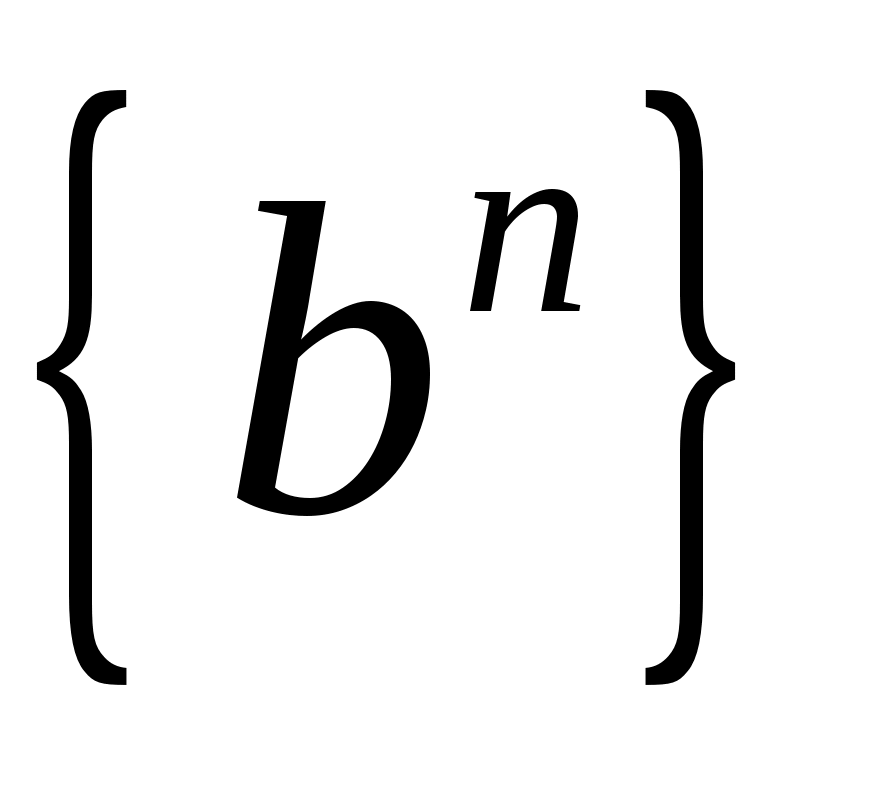 ведем линию действия вектора ведем линию действия вектора 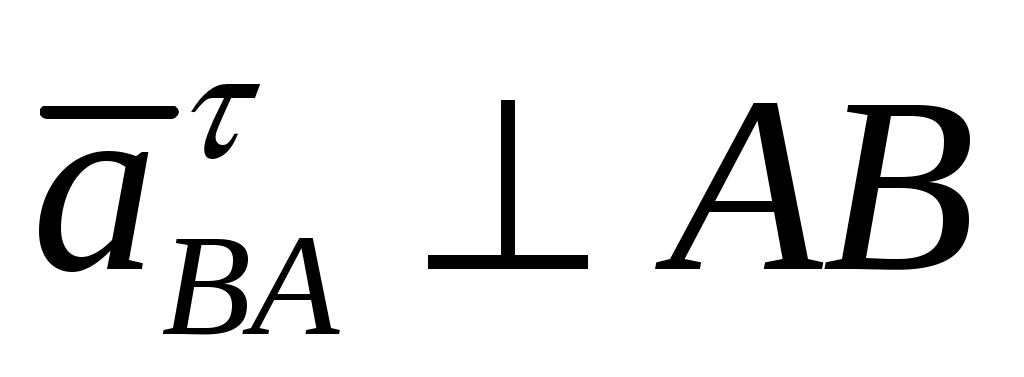 . Из плюса . Из плюса  откладываем отрезок откладываем отрезок 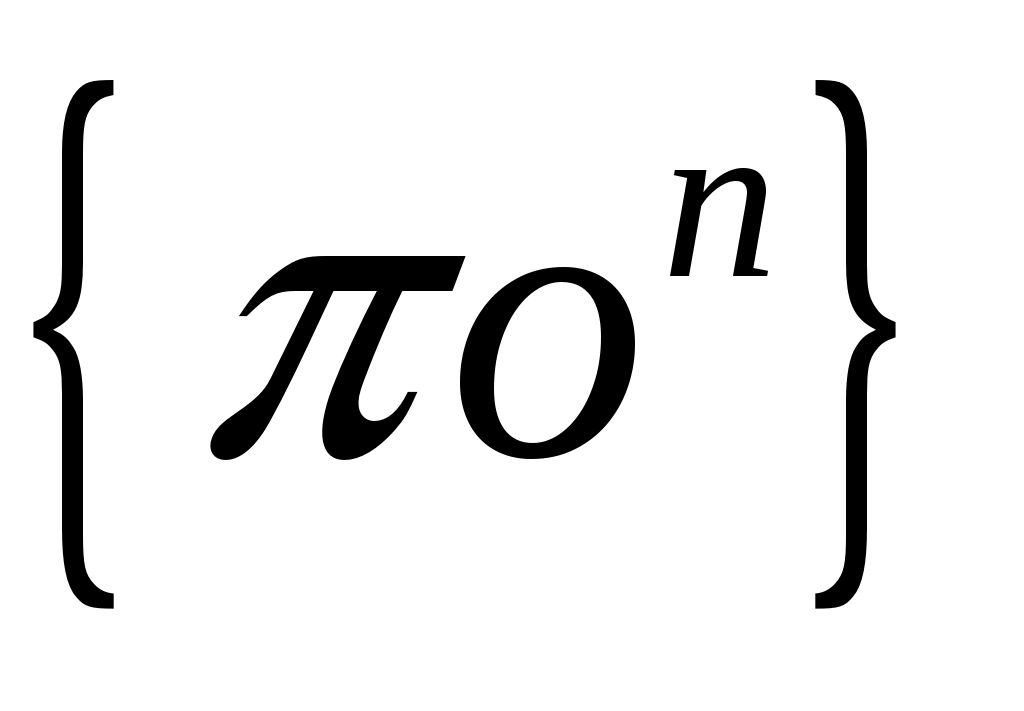 и из точки и из точки 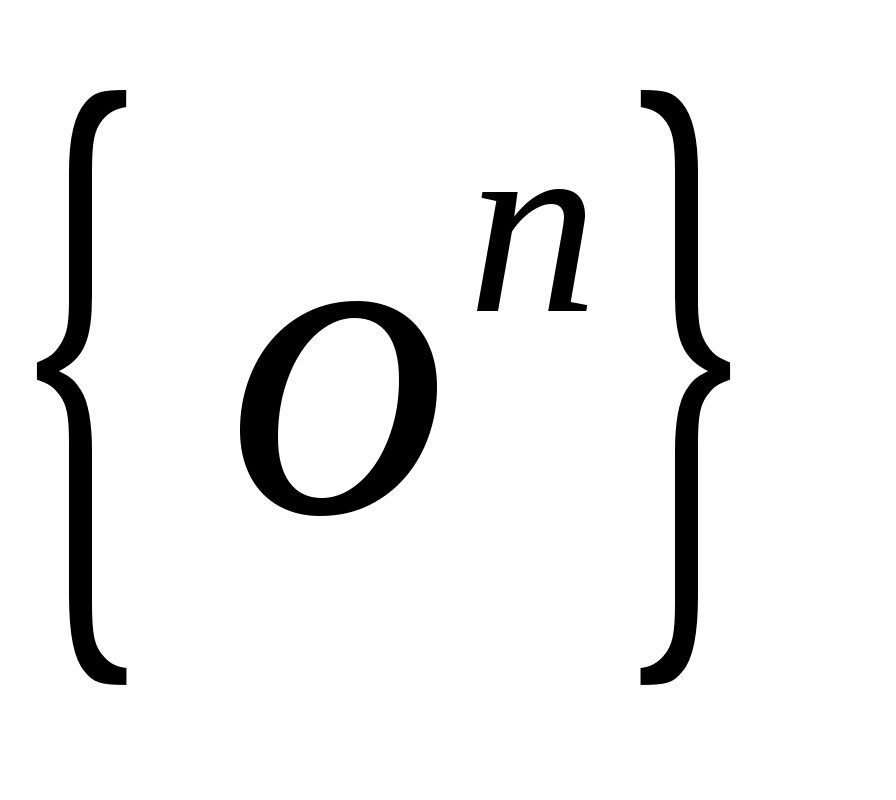 ведем линию действия вектора ведем линию действия вектора 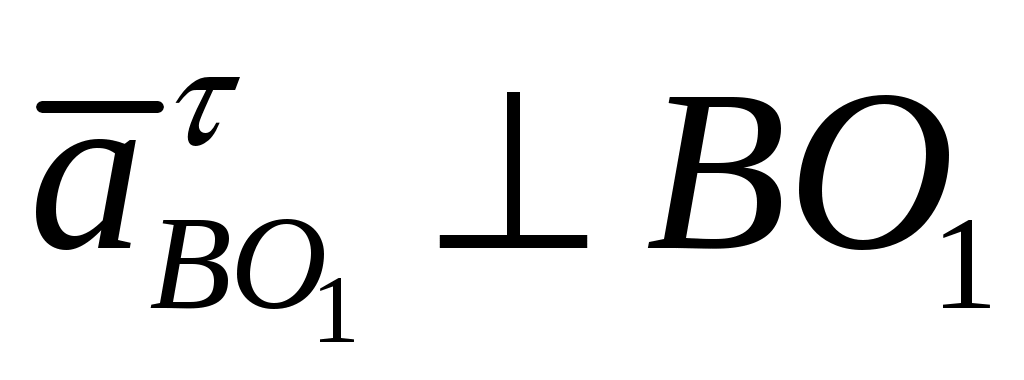 . .
Пересечение этих перпендикуляров дает точку 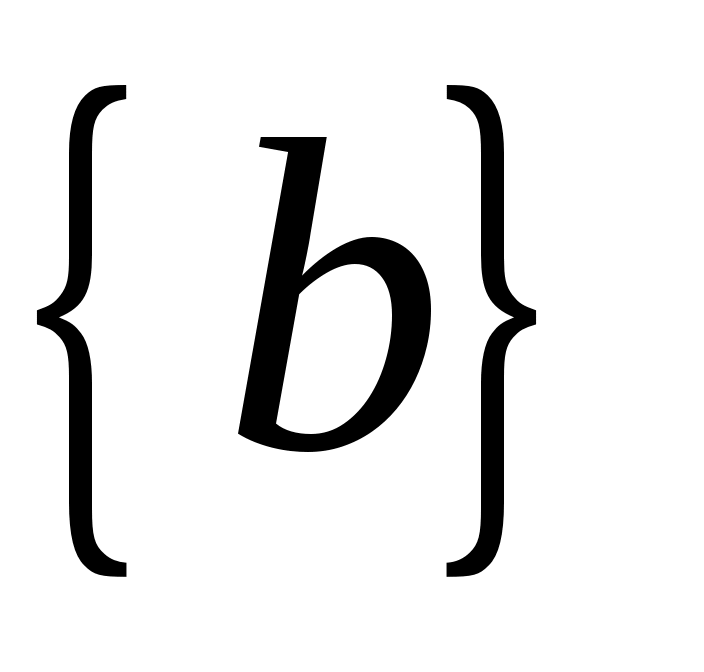 .Отрезки .Отрезки  и и 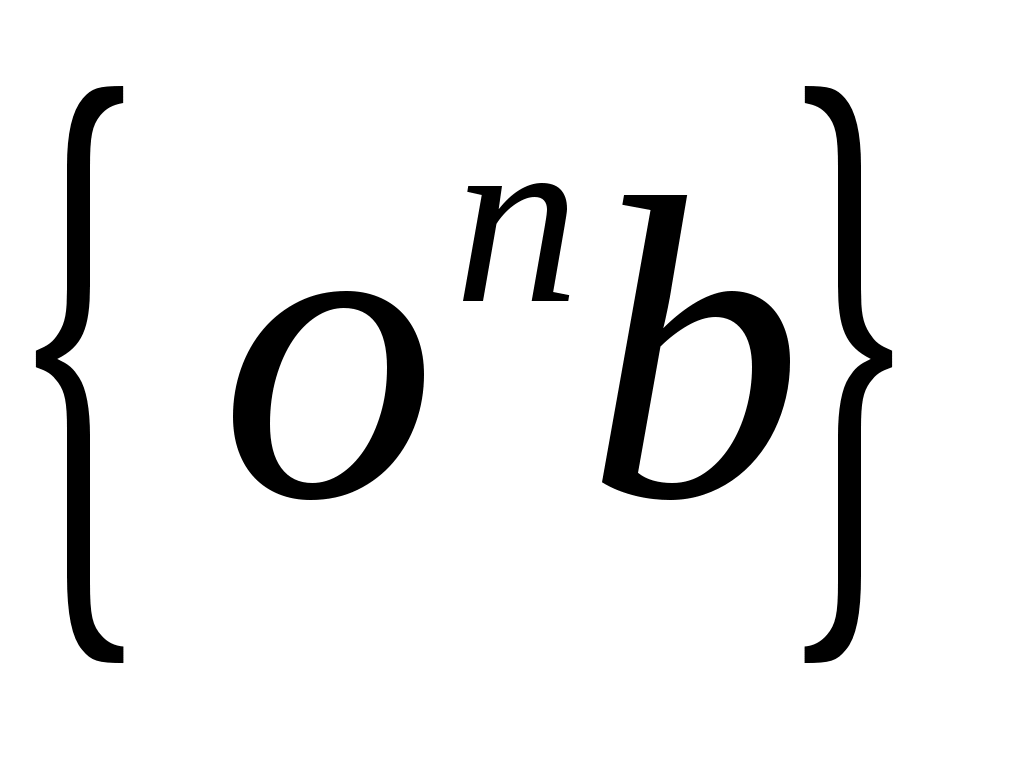 соответствуют относительным ускорениям соответствуют относительным ускорениям 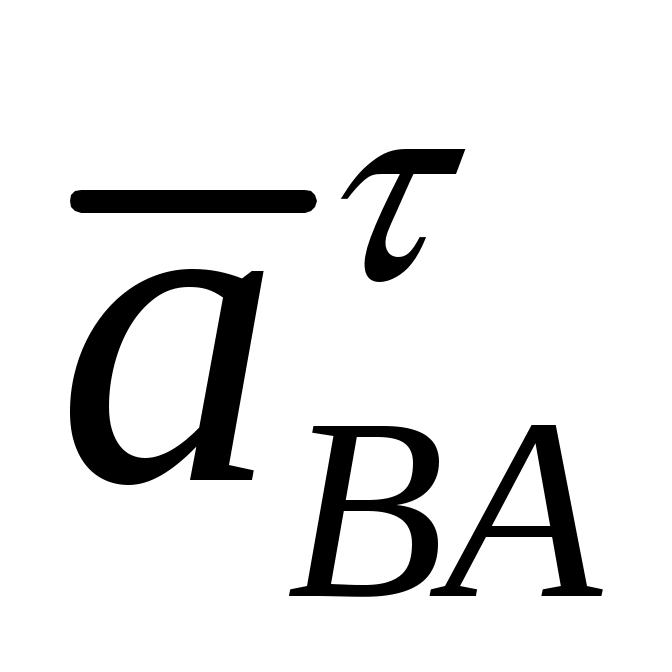 и и 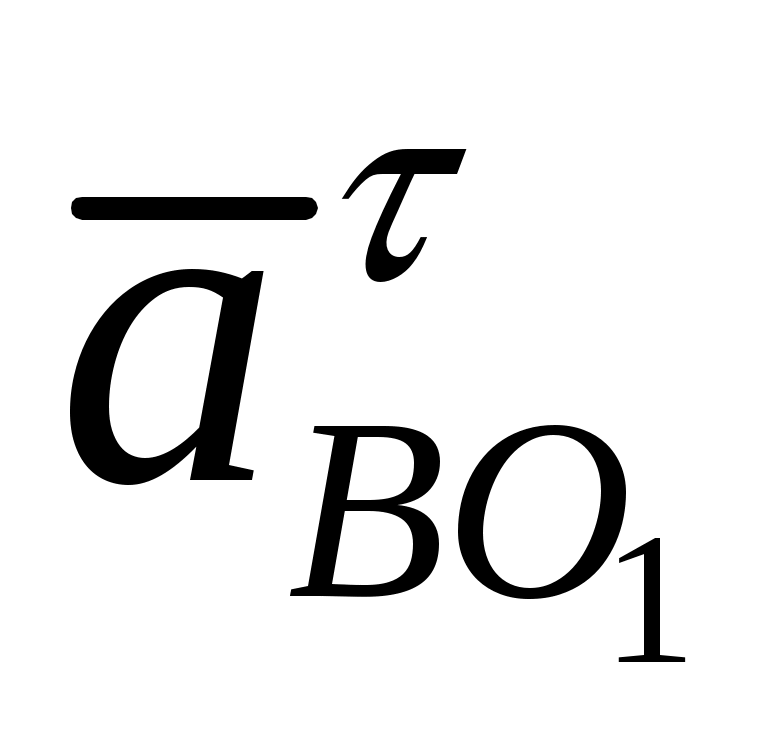 , а отрезок , а отрезок  - полному ускорению точки - полному ускорению точки 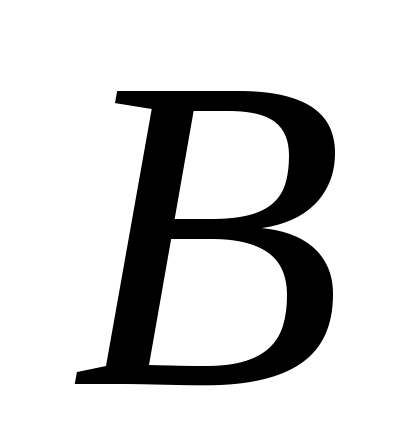 . .
Численные значения тангенциальных составляющих и полного ускорения:
 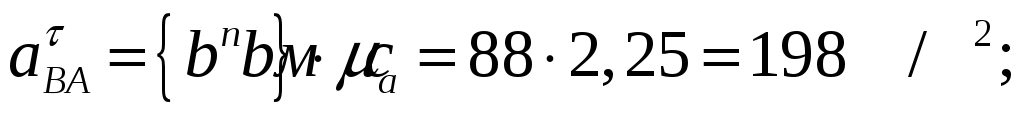
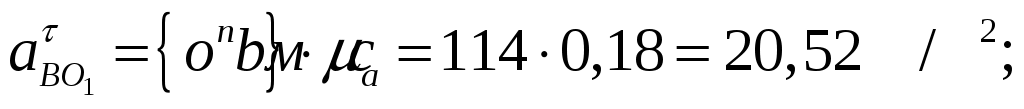
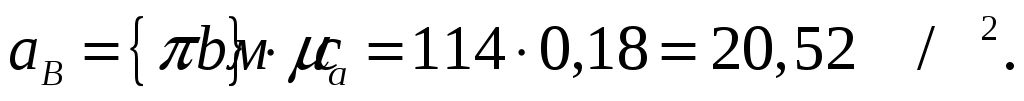
Для определения скорости точки 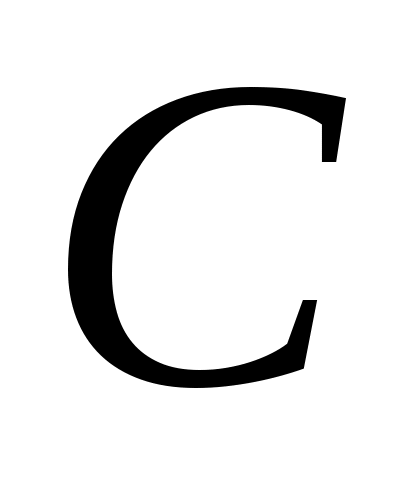 воспользуемся принципом подобия плана скоростей и плана механизма, согласно которому точки звена расположены подобно соответствующим точкам плана. Поскольку в механизме точка С находится на 1/3 звена ВС, то и на плане скоростей воспользуемся принципом подобия плана скоростей и плана механизма, согласно которому точки звена расположены подобно соответствующим точкам плана. Поскольку в механизме точка С находится на 1/3 звена ВС, то и на плане скоростей 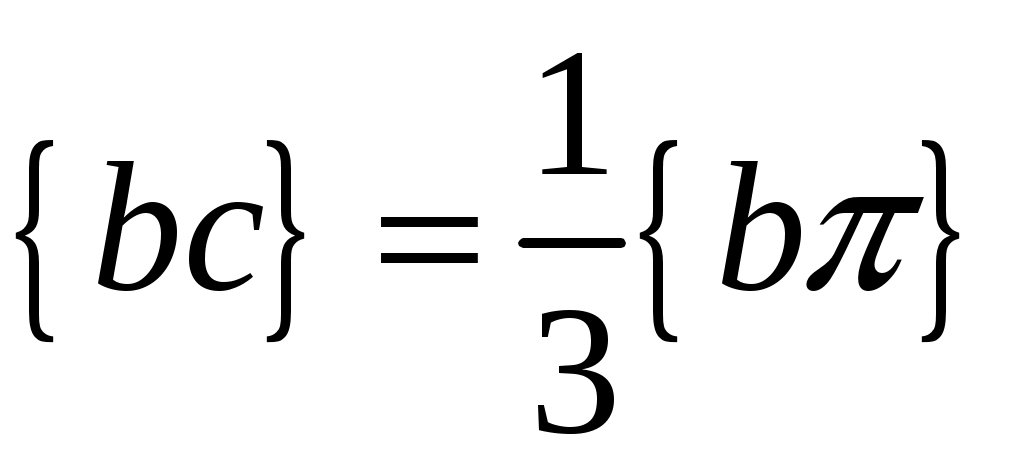
Ускорение точки 
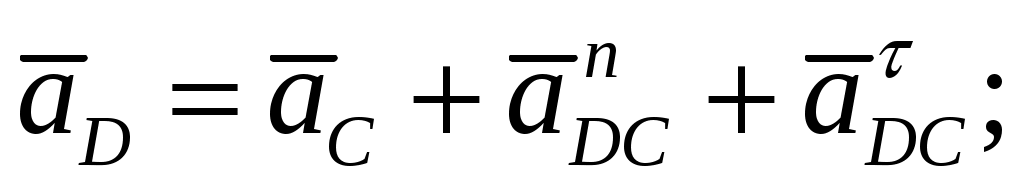
Вектор 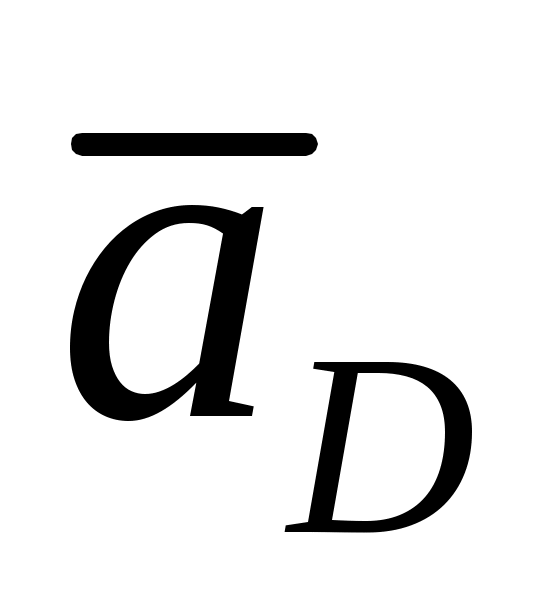 направлен параллельно направляющим ползуна. Вектор нормальной составляющей направлен параллельно направляющим ползуна. Вектор нормальной составляющей 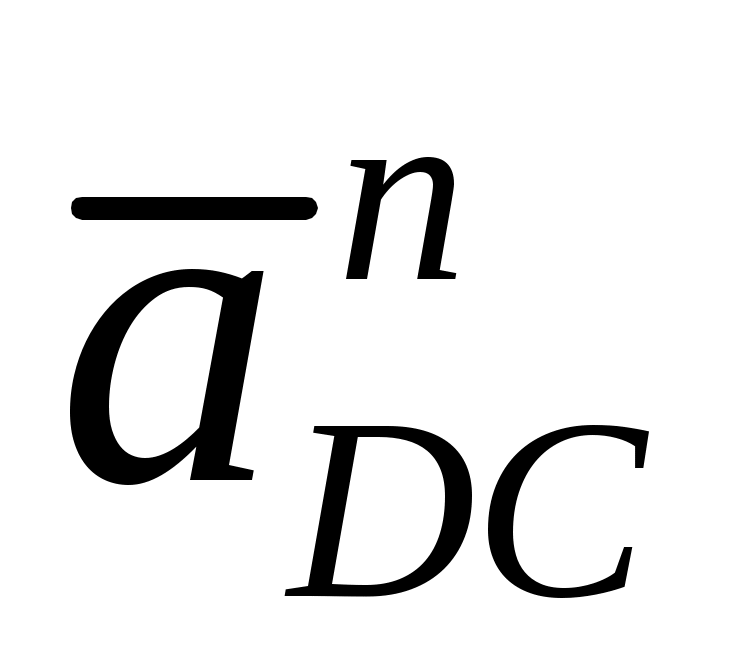 направлен параллельно, а тангенциальной составляющей направлен параллельно, а тангенциальной составляющей 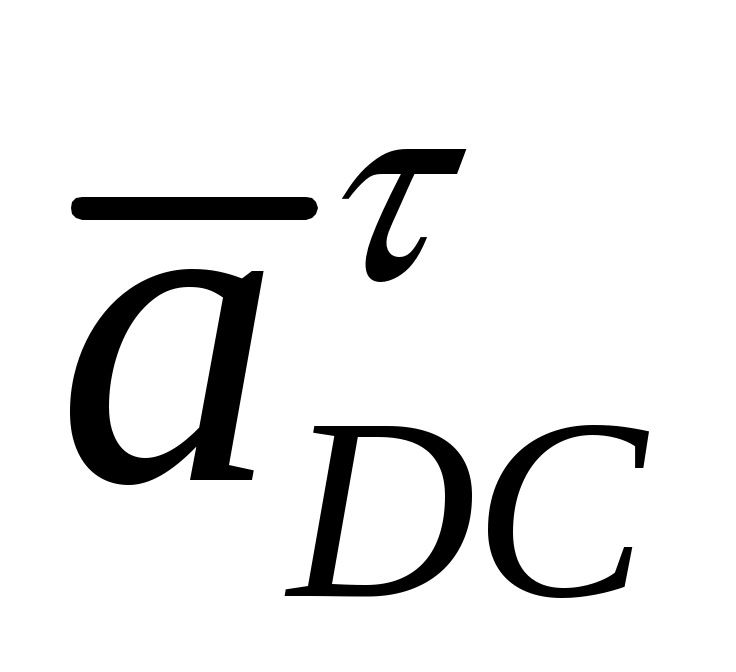 - перпендикулярно звену - перпендикулярно звену 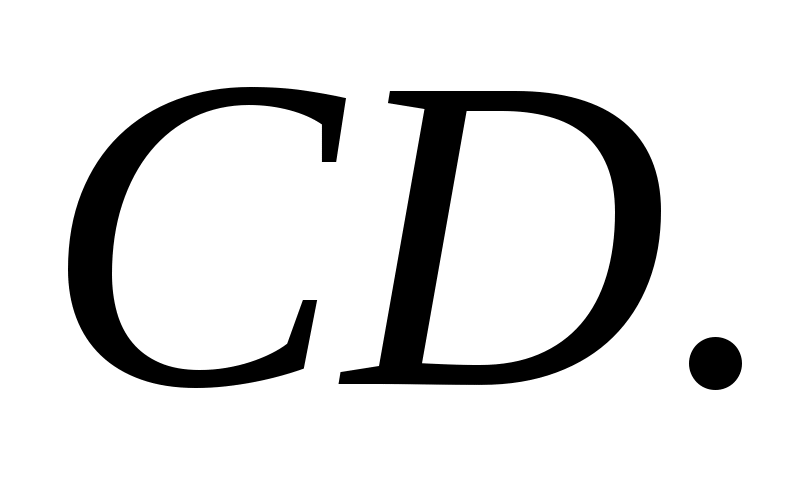
Численные значение нормальной составляющей:
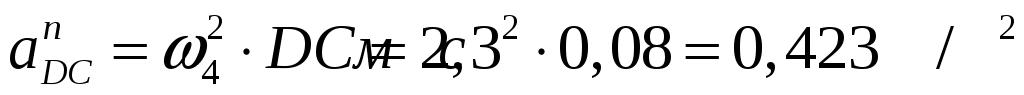
Из полюса  плана проводим линию, параллельную направляющей ползуна. Параллельно звену плана проводим линию, параллельную направляющей ползуна. Параллельно звену  откладываем отрезок откладываем отрезок 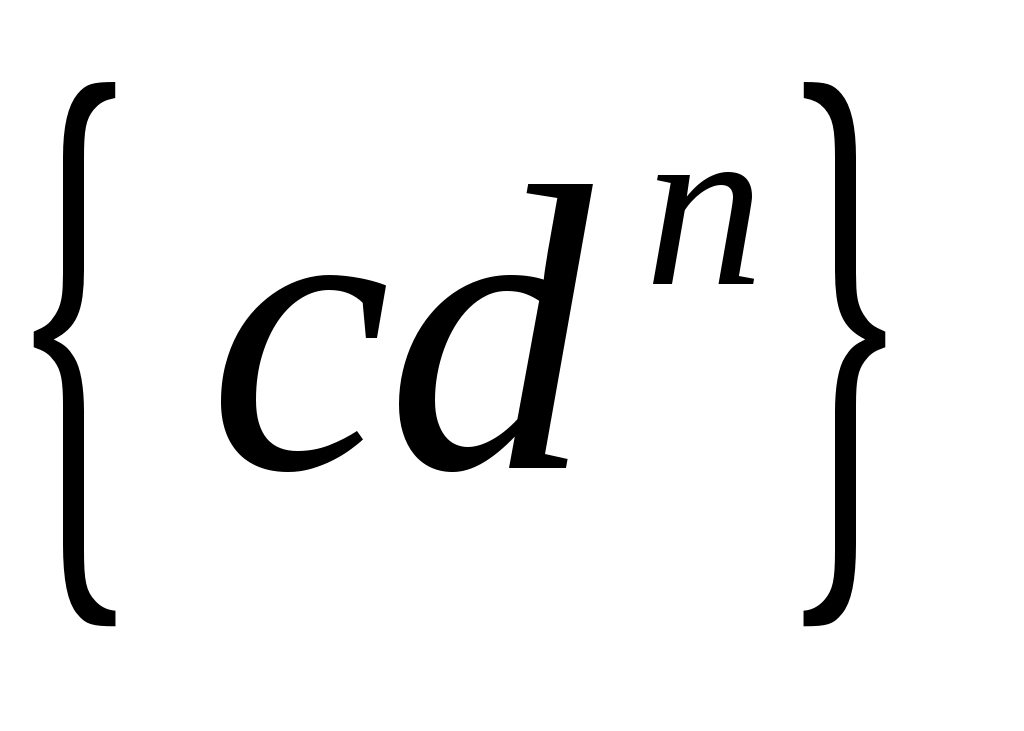 , равный: , равный:
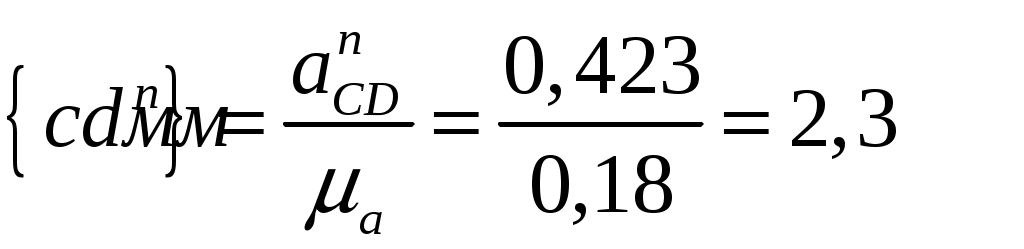 , ,
к концу которого проводим перпендикуляр. Пересечение этого перпендикуляра с линией, параллельной направляющей ползуна дает нам точку 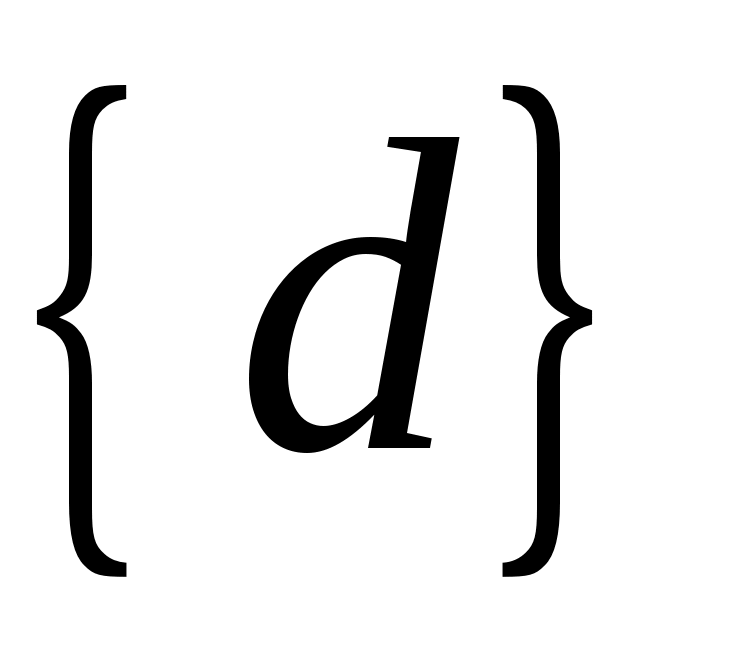 . Отрезок . Отрезок  соответствует ускорению точки соответствует ускорению точки 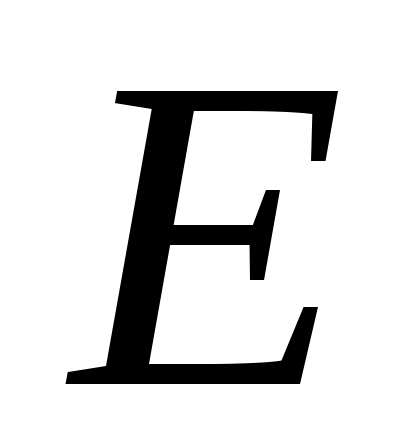 , а отрезок , а отрезок 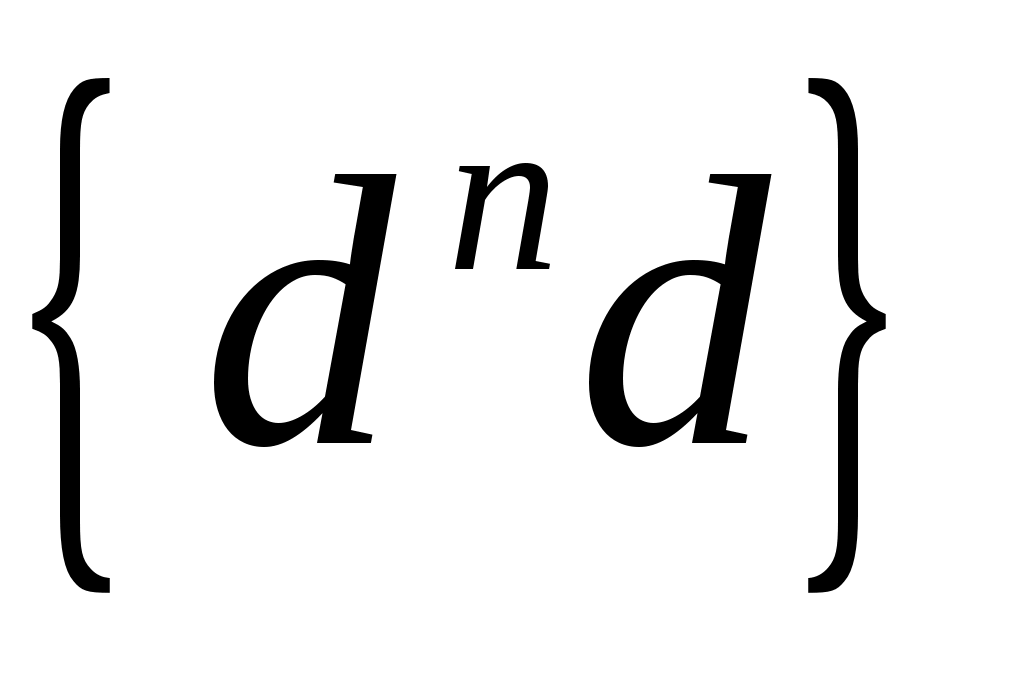 - тангенциальной составляющей относительного ускорения. - тангенциальной составляющей относительного ускорения.
Численные значение полного ускорения и тангенциальной составляющей:
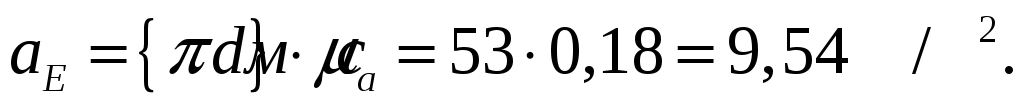
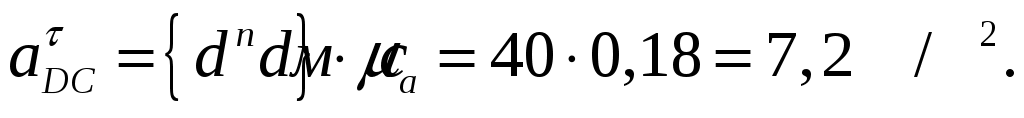
 Используя принцип подобия строим на плане скорости центров масс звеньев. Центры масс расположены на серединах звеньев, значит и на плане скоростей они будут расположены на серединах отрезков, соответствующих звеньям. Используя принцип подобия строим на плане скорости центров масс звеньев. Центры масс расположены на серединах звеньев, значит и на плане скоростей они будут расположены на серединах отрезков, соответствующих звеньям.
Численные значение тангенциальной составляющей:
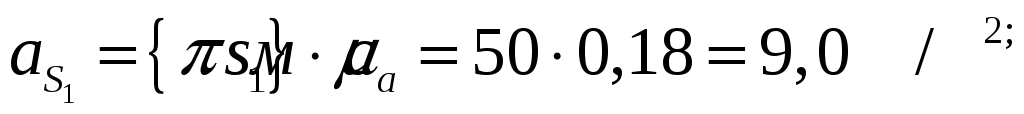
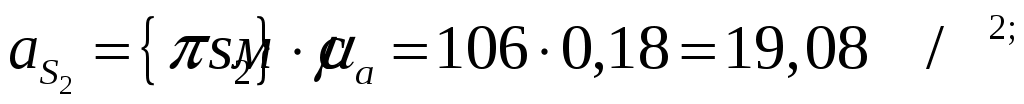
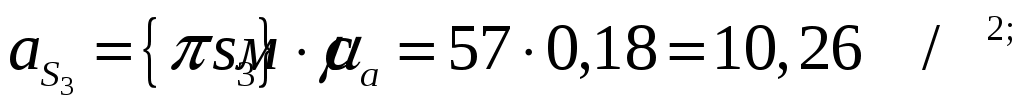
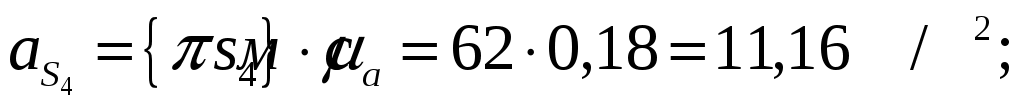
Угловые ускорения звеньев механизма:
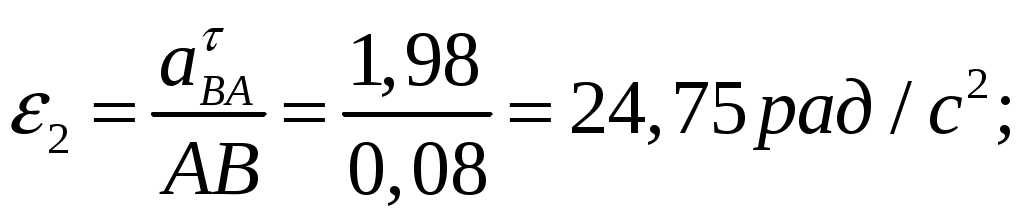
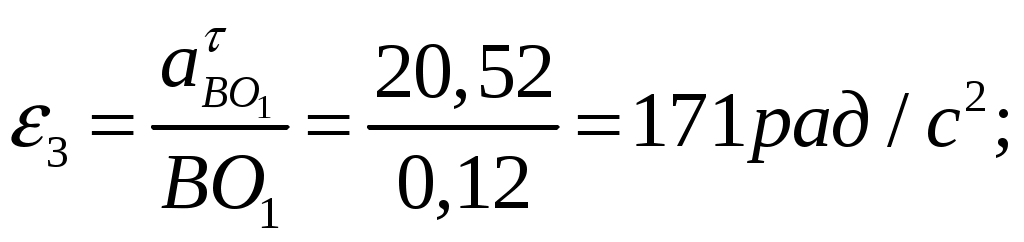
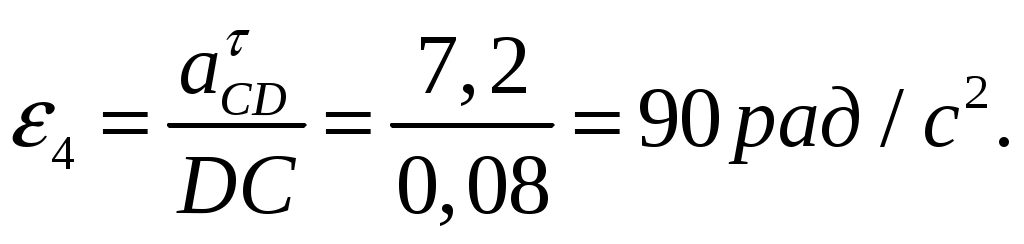


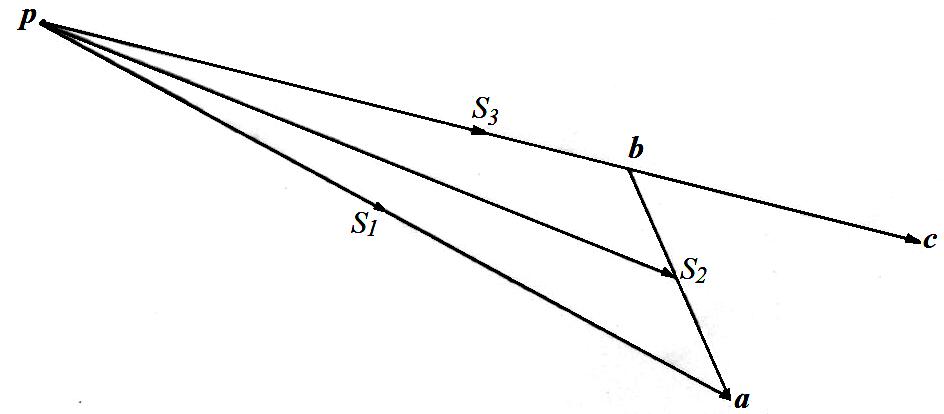
Рис. План скоростей 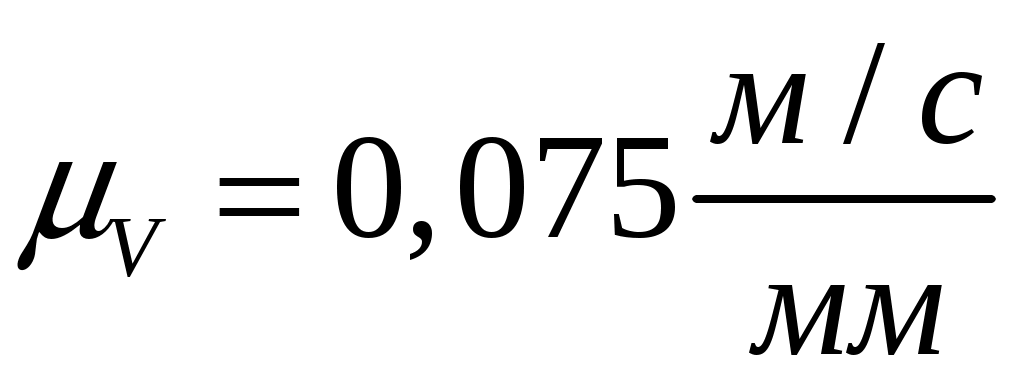
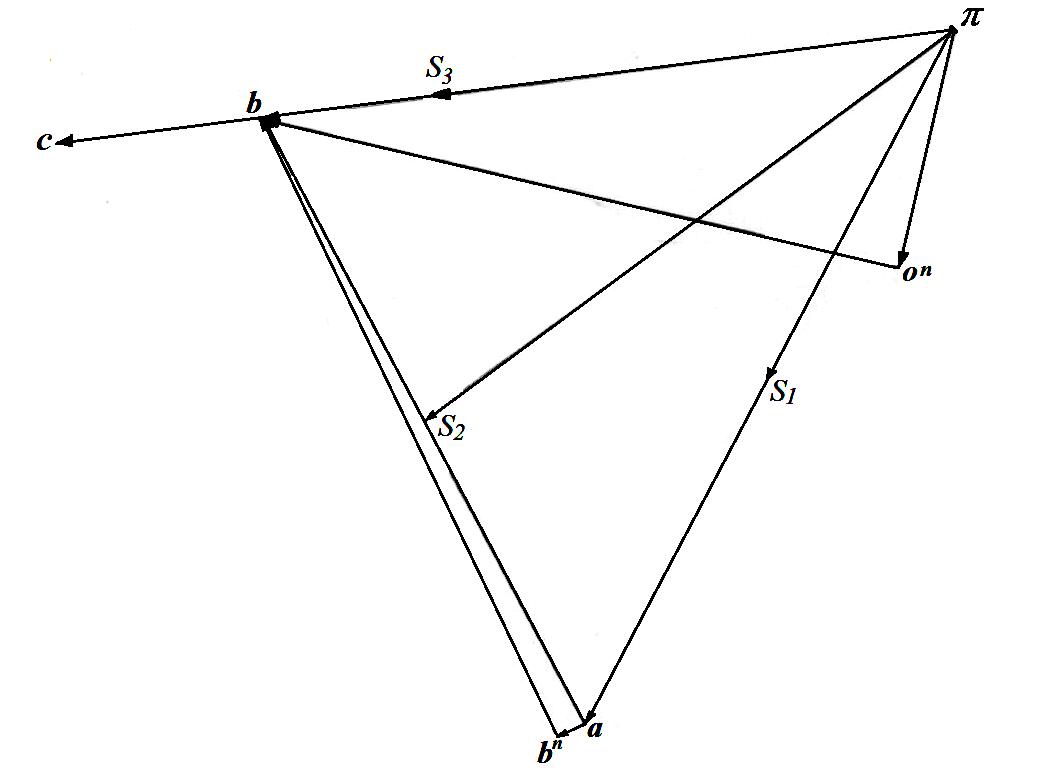
Рис. План ускорений 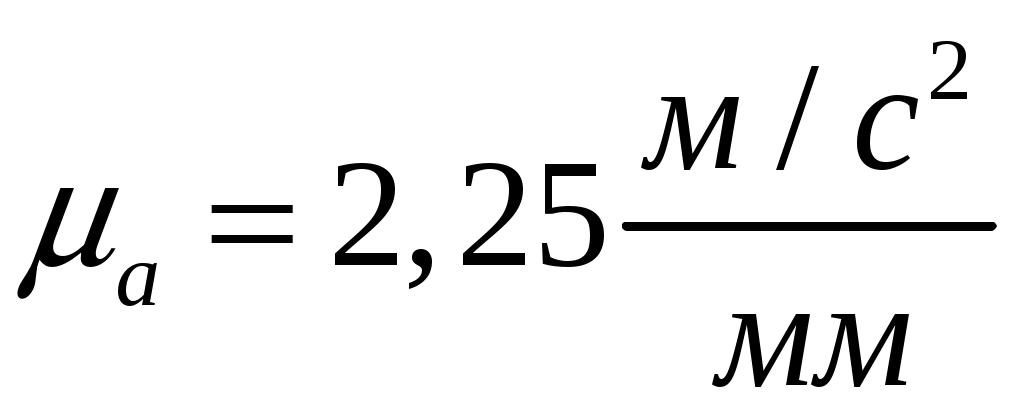
 . .
3.1 Задача исследования.
- Расчет всех действующих сил;
- Построение планов сил;
- Определение уравновешивающей силы.
3.2 Расчет всех действующих сил.
- Силы инерции
Звено 1 – кривошип.
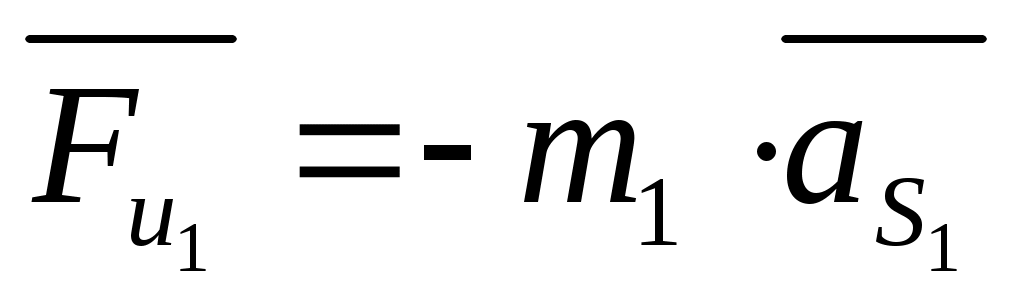 , ,
где: 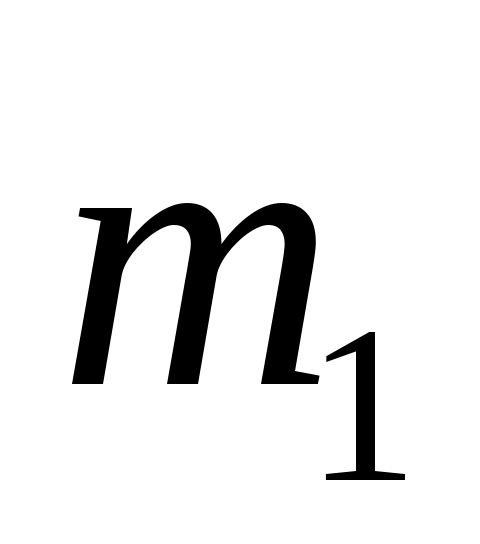 - масса кривошипа. - масса кривошипа.
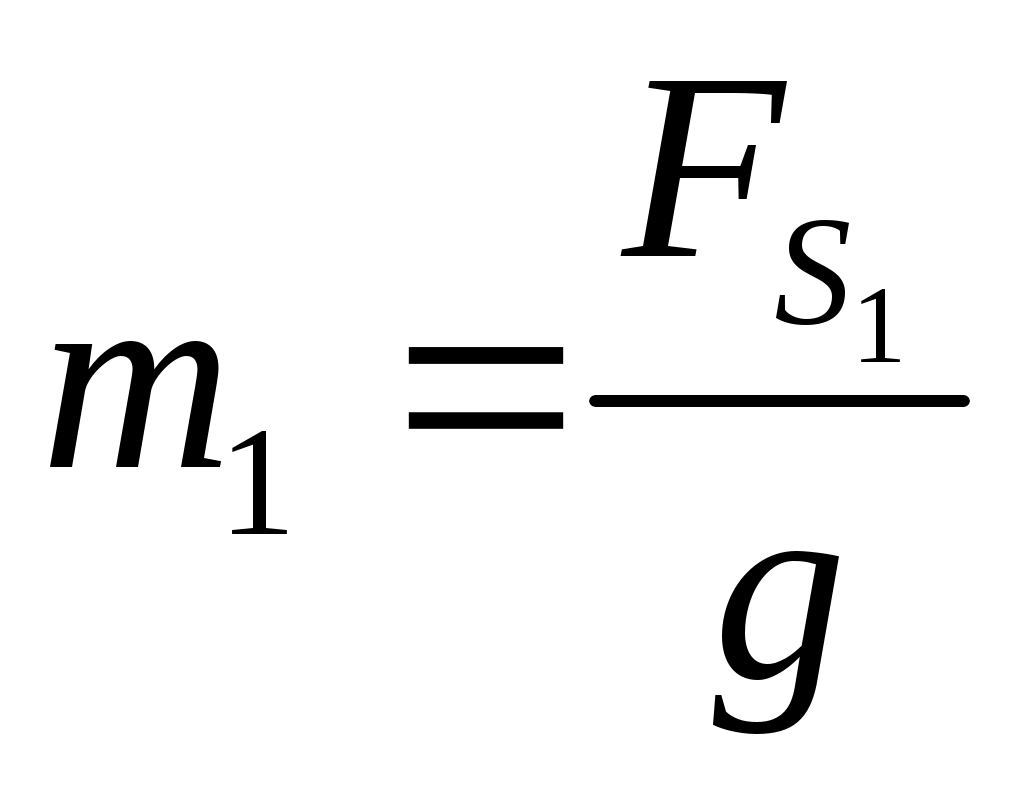 . .
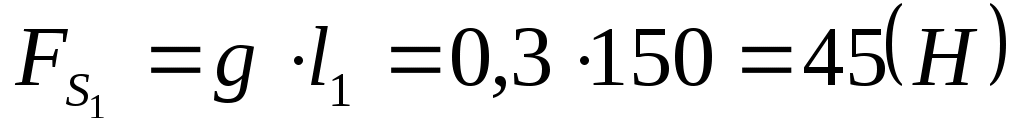 - вес кривошипа. - вес кривошипа.
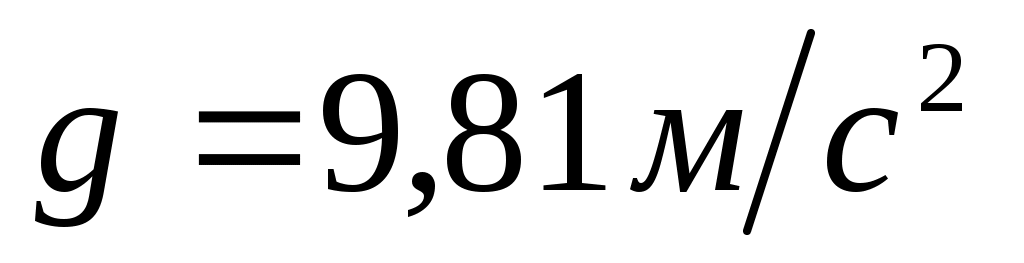 - ускорение свободного падения. - ускорение свободного падения.
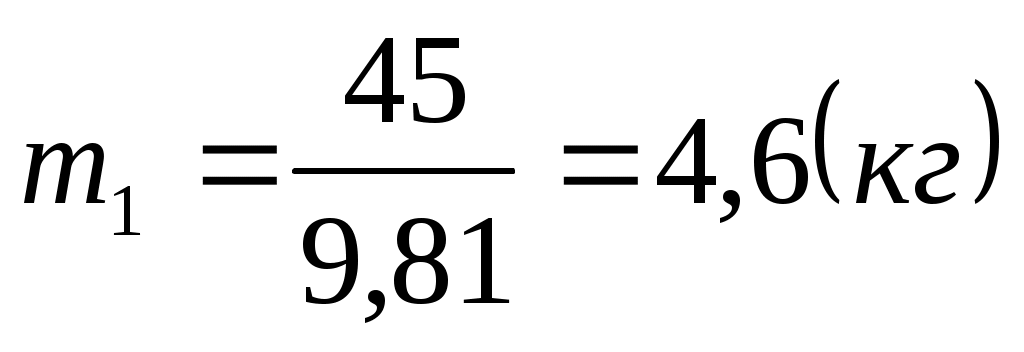 . .
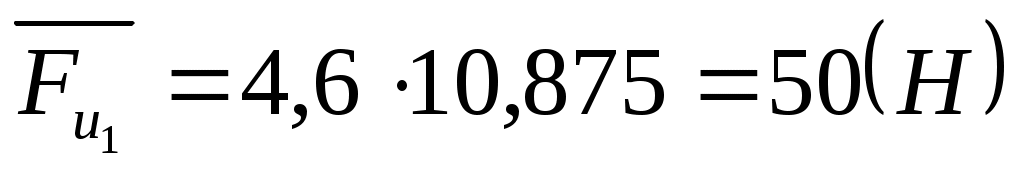 . .
Звено 2 - шатун.
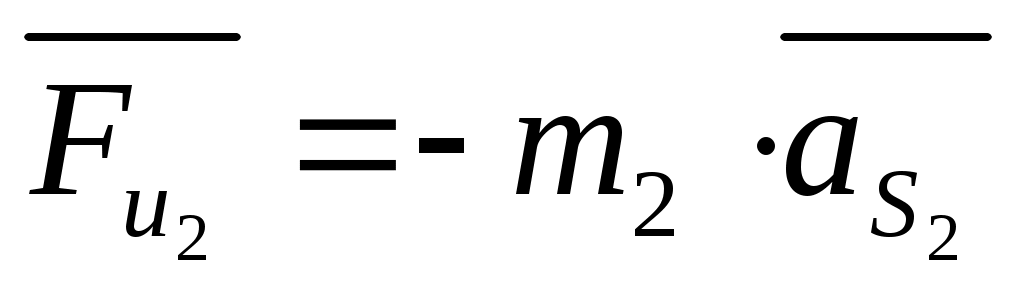 , ,
где: 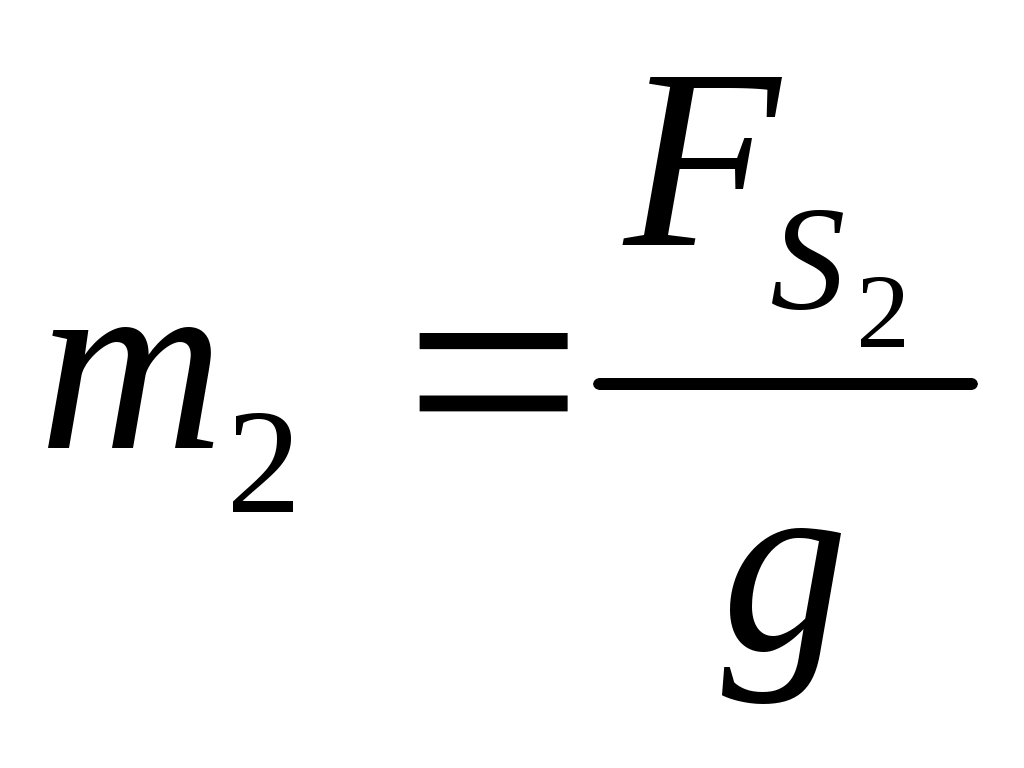 . .
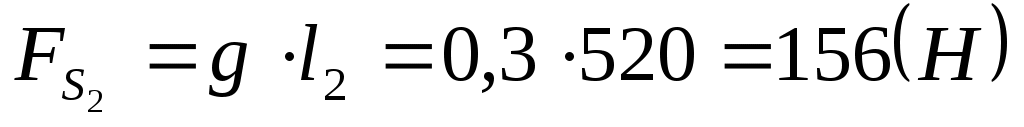 . .
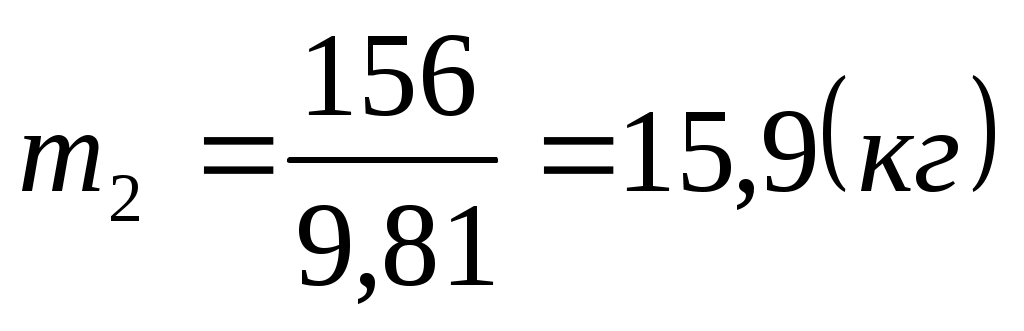 . .
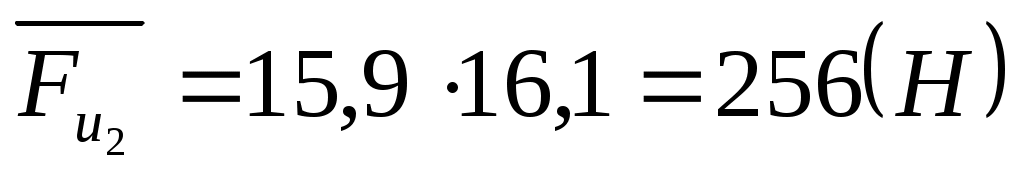 . .
Звено 3 - коромысло.

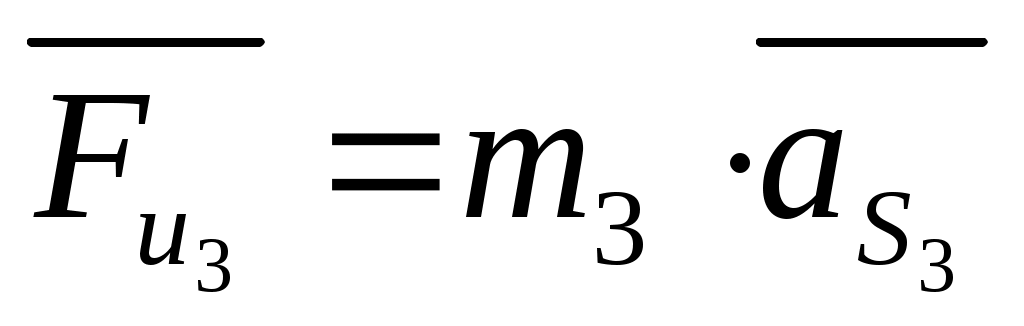 , ,
где: 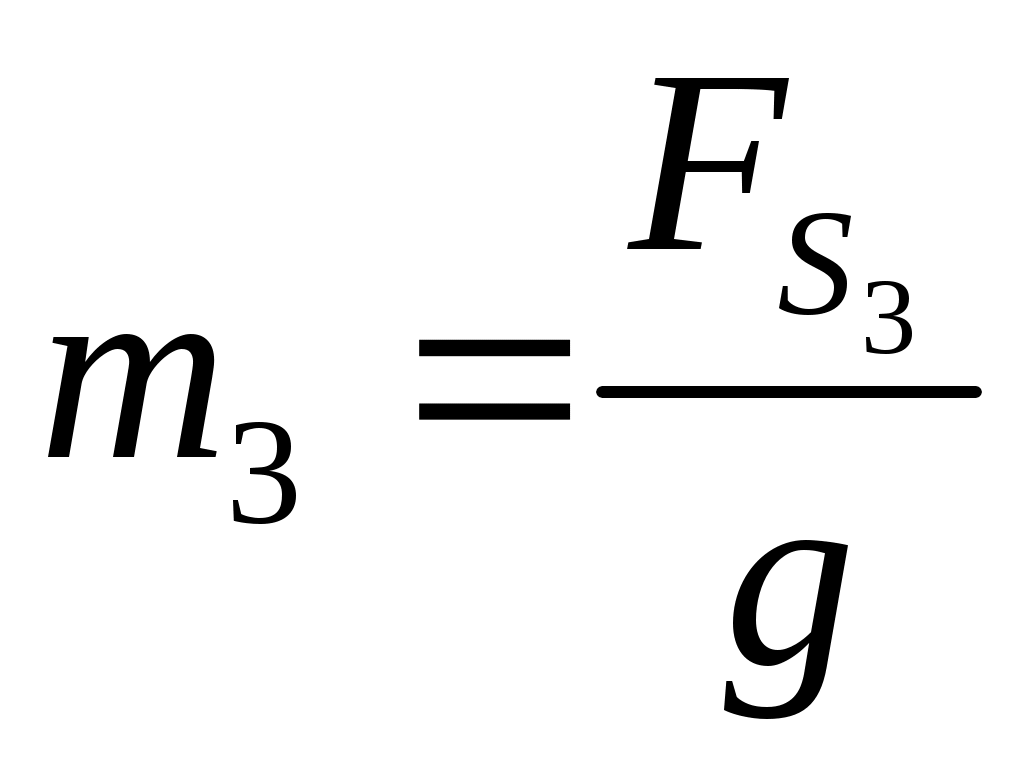 . .
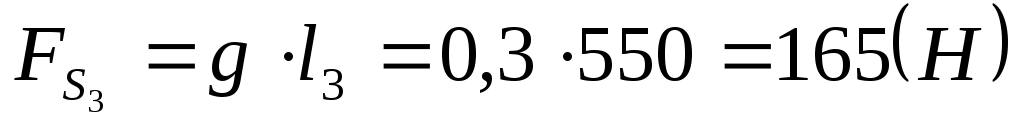 . .
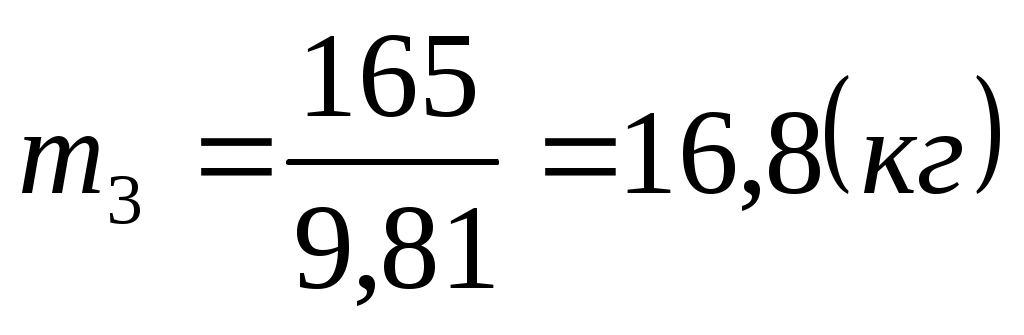 . .
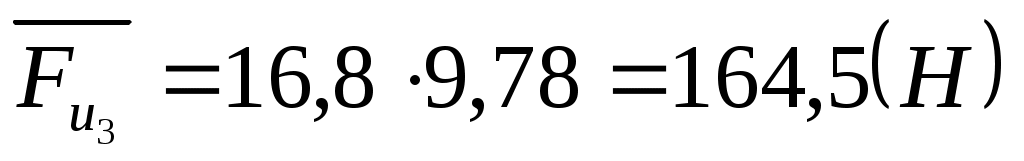 . .
- Главные моменты сил инерций.
Звено 1.
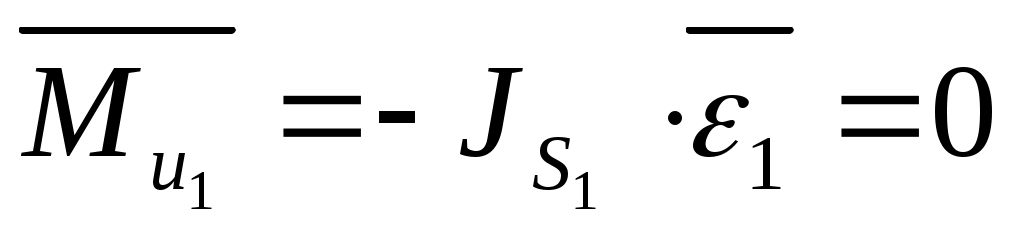 - т.к. при постоянной скорости вращения угловое ускорение - т.к. при постоянной скорости вращения угловое ускорение 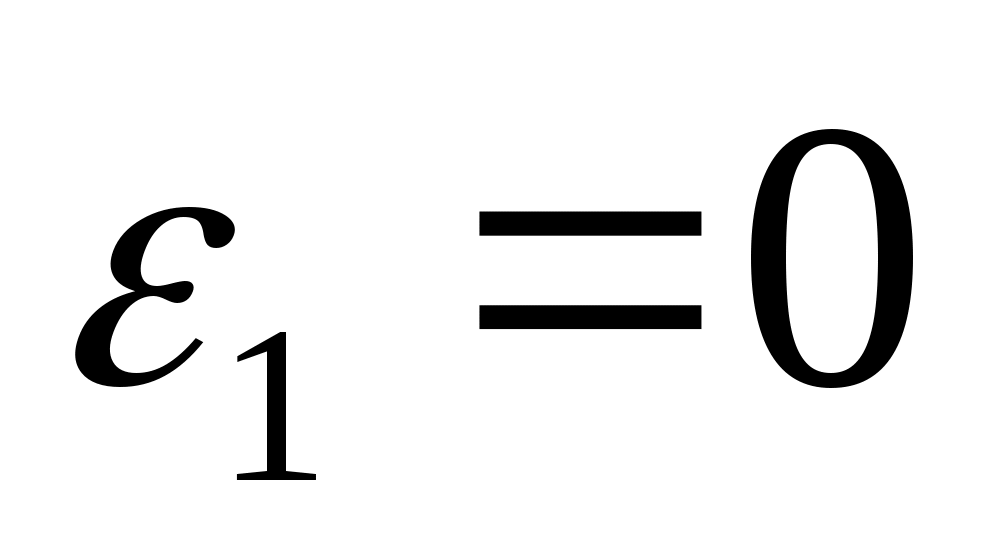 . .
Звено 2.
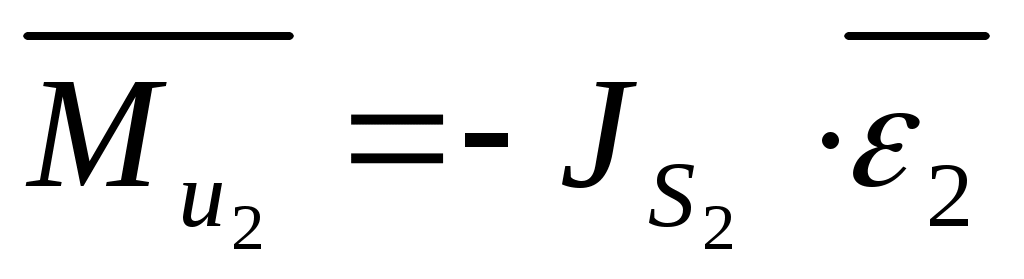 , ,
где: 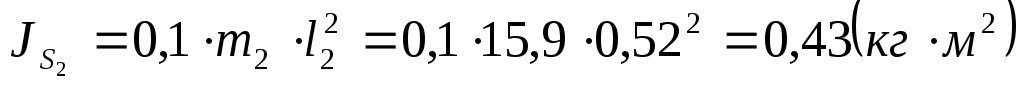 . .
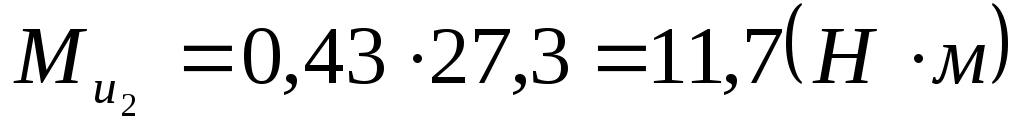 . .
Представим моменты сил инерции шатуна эквивалентной парой сил, с плечом, равным длине шатуна 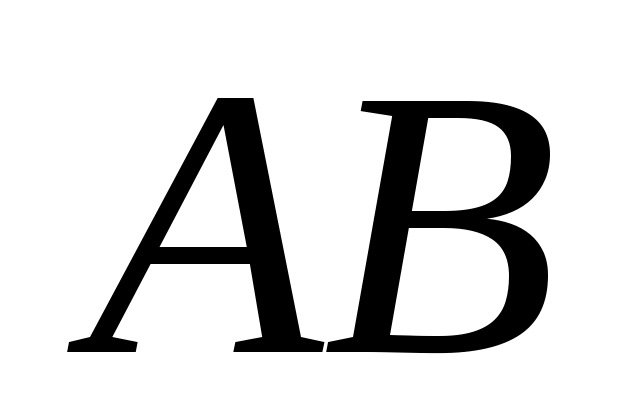 . .
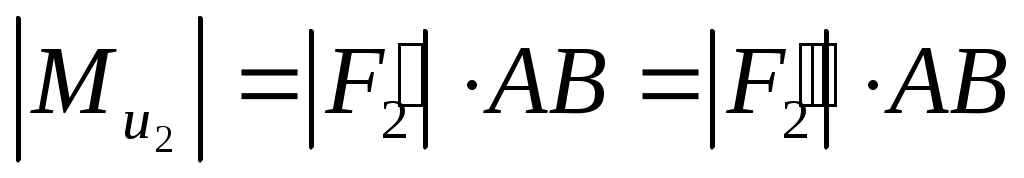 , откуда: , откуда:
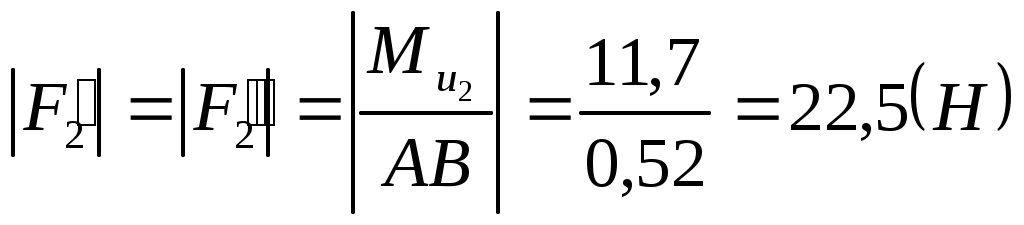 . .
Звено 3.
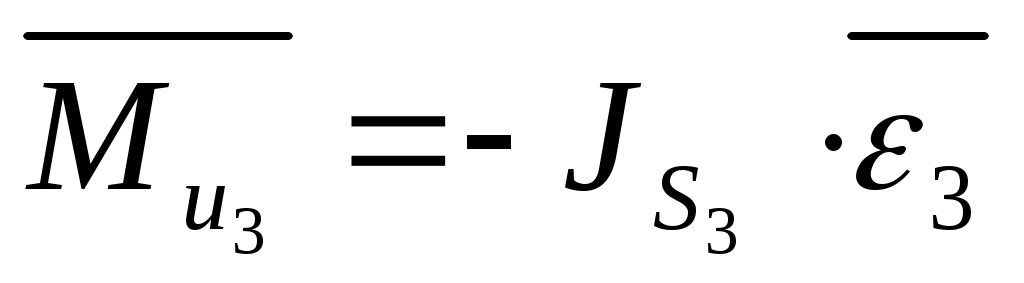 , ,
где: 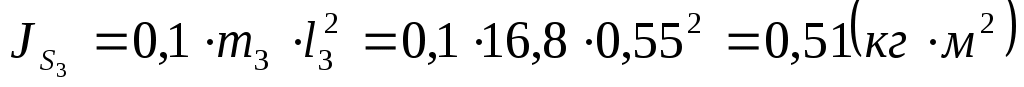 . .
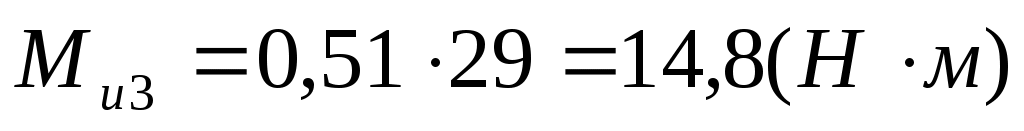
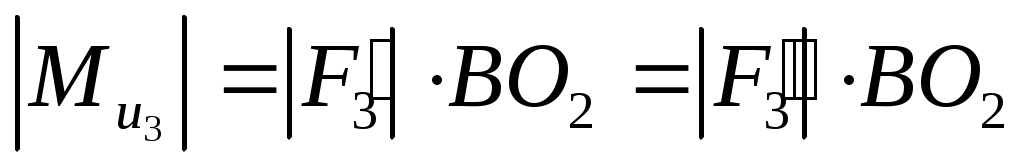

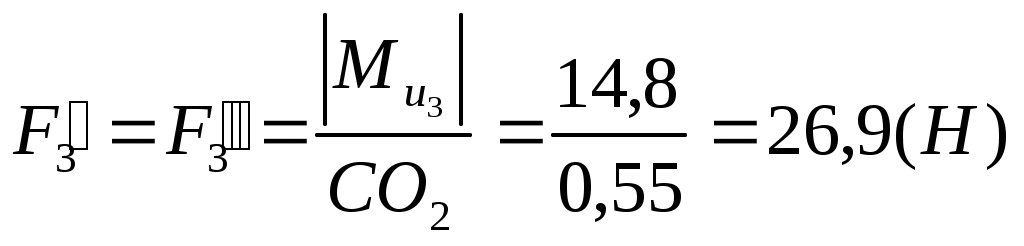 . .
3.3.Построение планов сил 3.3.1 Расчет группы Ассура 3-2.
Механизм состоит из исходного звена 1 и одной двухповодковой структурной группы второго класса группы Асура 3-2.
Расчет начинаем со структурной группы Ассура 3-2.
На группу действуют известные по значению и направлению силы: 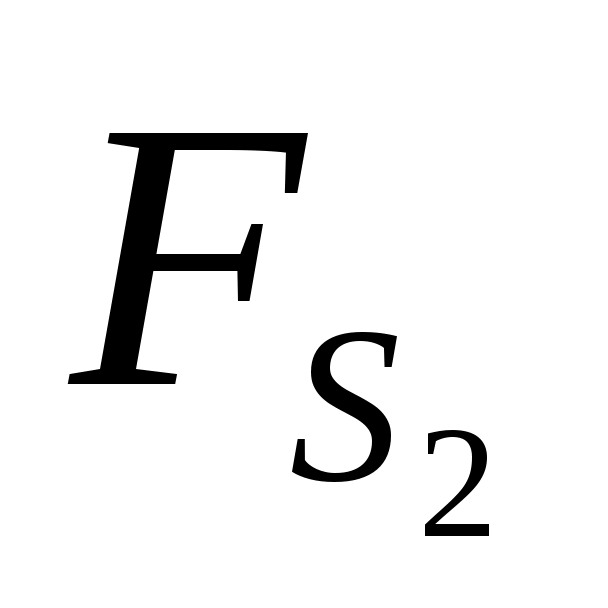 , , 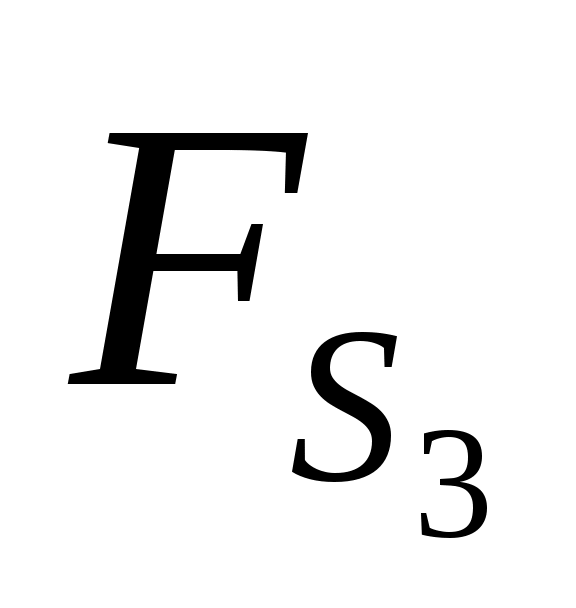 , , 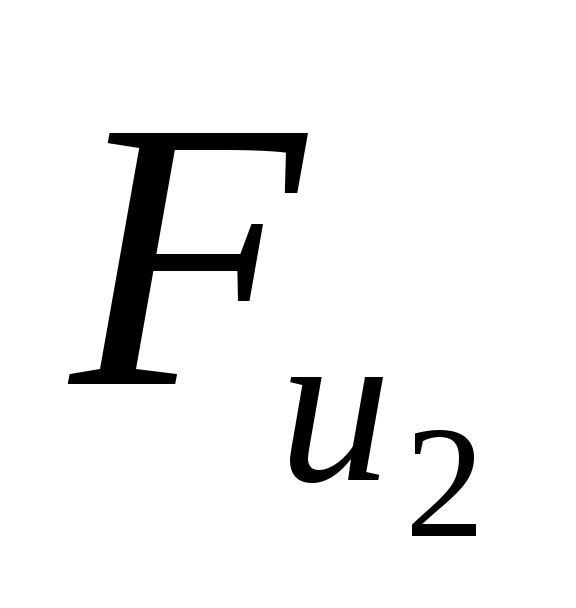 , , 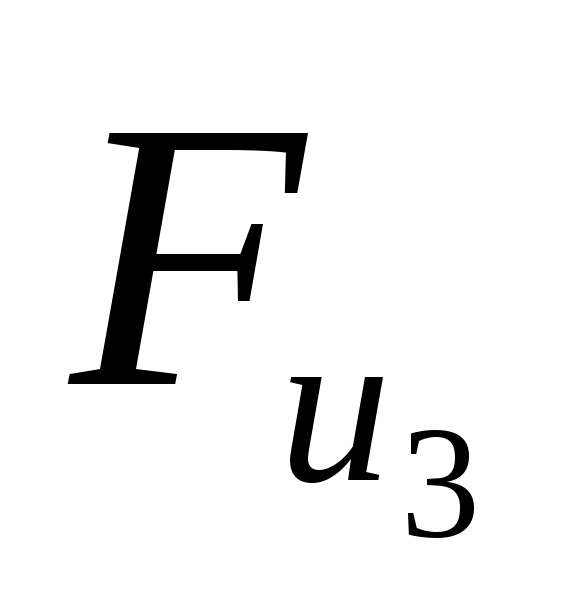 , , 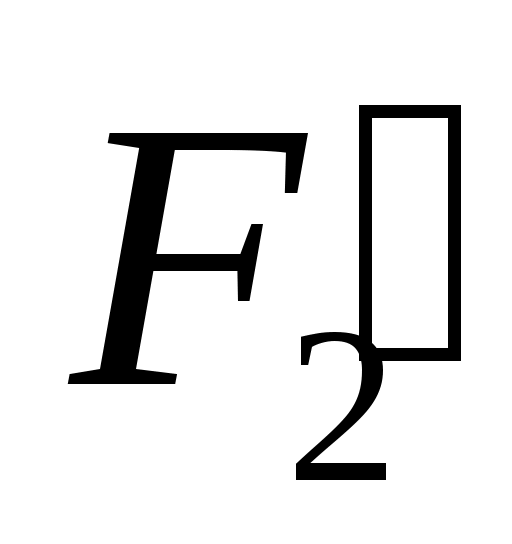 , , 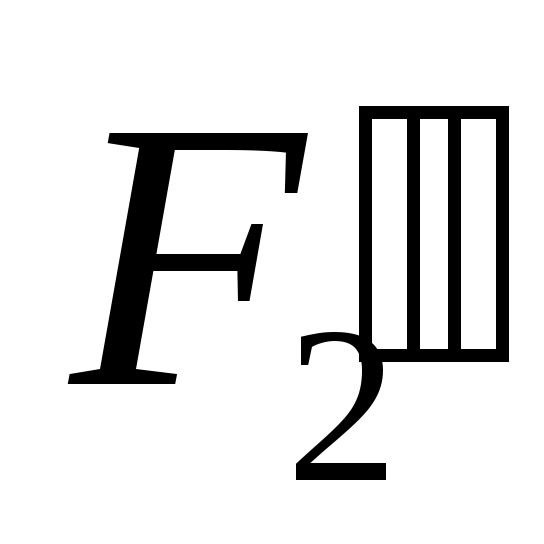 , ,  , ,  , ,  . .
Освобождаем группу от связей и прикладываем вместо них реакции.
Силы реакций шарниров представляем в виде двух составляющих вдоль звена и перпендикулярно звену:
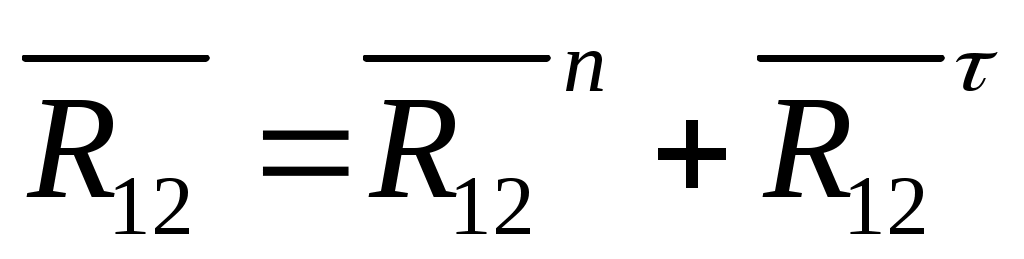
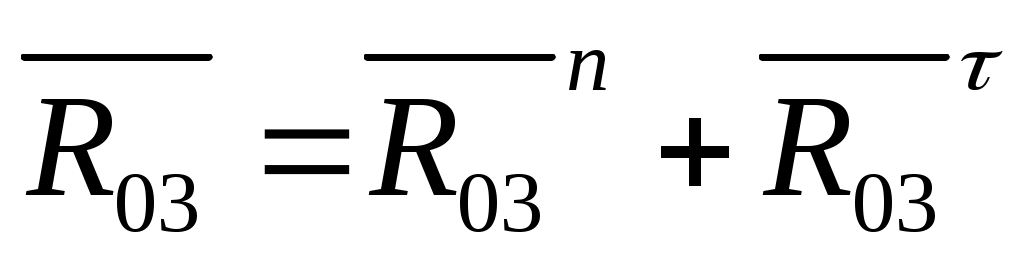 . .
Аналитические уравнения равновесия:
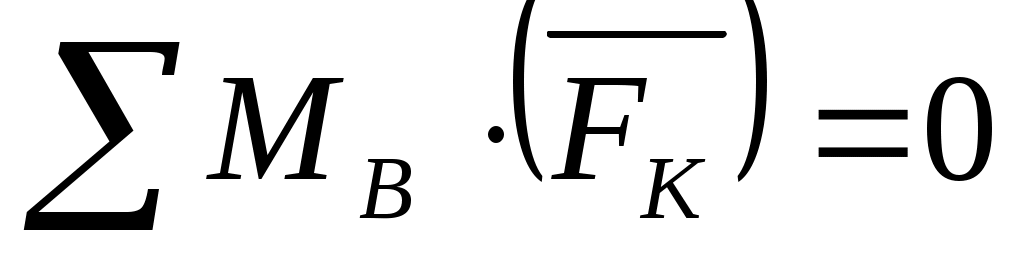 - для звена 2. - для звена 2.
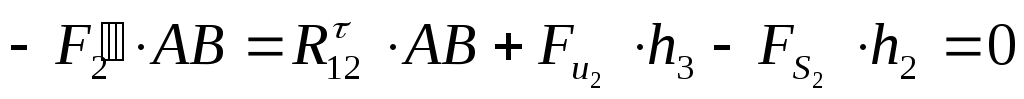 , ,
где: 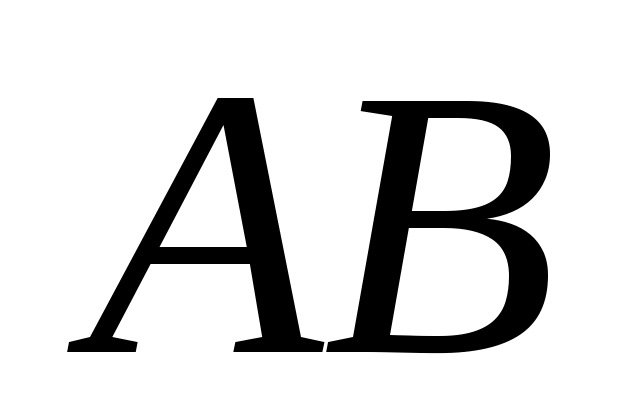 , , 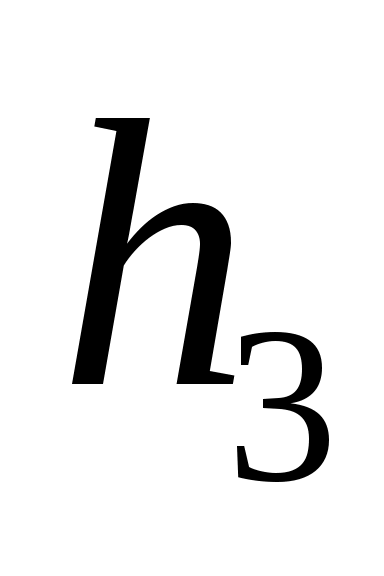 , , 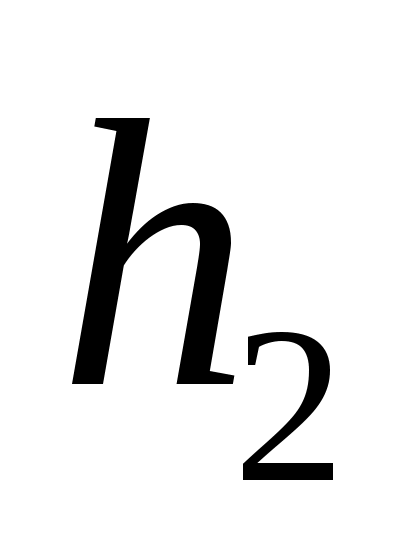 - плечи сил взятые с чертежа в мм. - плечи сил взятые с чертежа в мм.
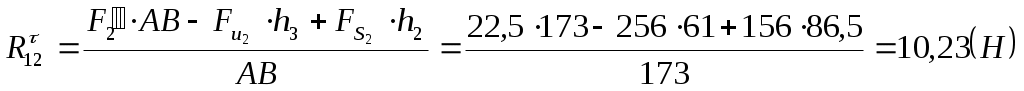 . .
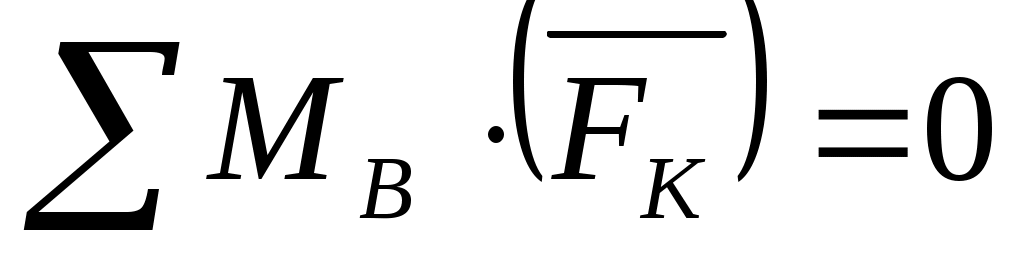 - для звена 3. - для звена 3.
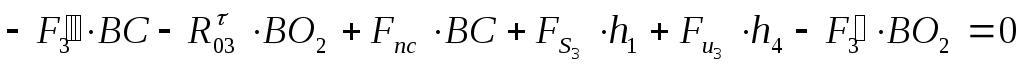 , ,
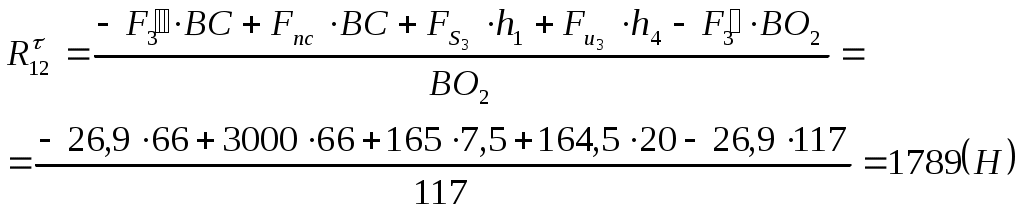 . .
Векторное уравнение равновесия для всей группы:
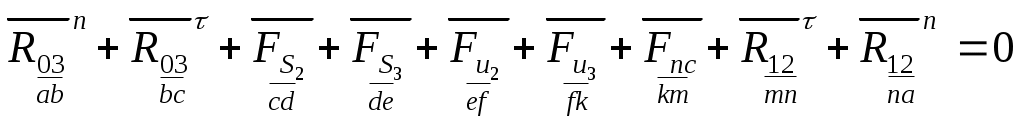 . .

Силы от моментов инерции в управление не включаем, поскольку при графическом построении они уравновешиваются.
По векторному уравнению строим план сил группы Ассура.
Масштабный коэффициент.
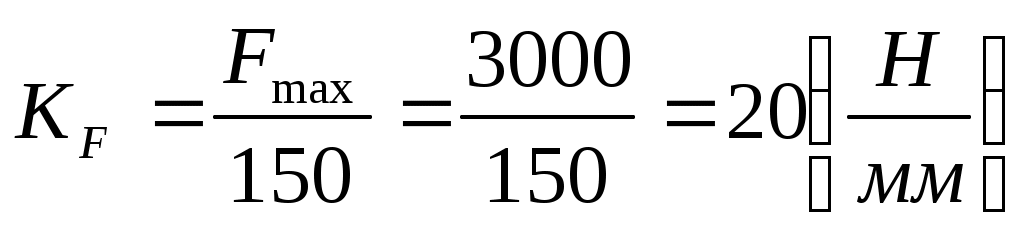 . .
Длины остальных векторов на плане определим, поделив их модули на масштабный коэффициент.
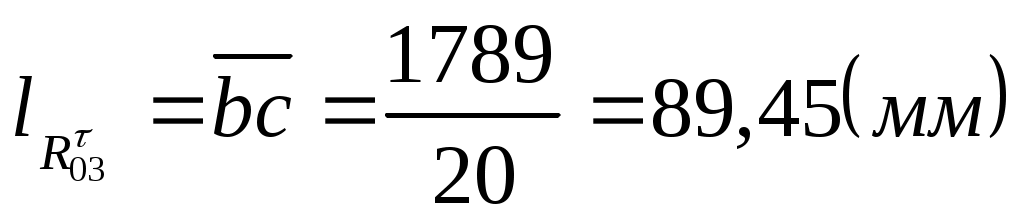 . .
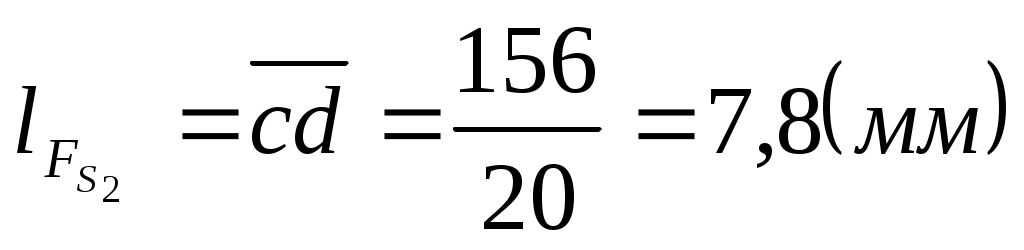 . .
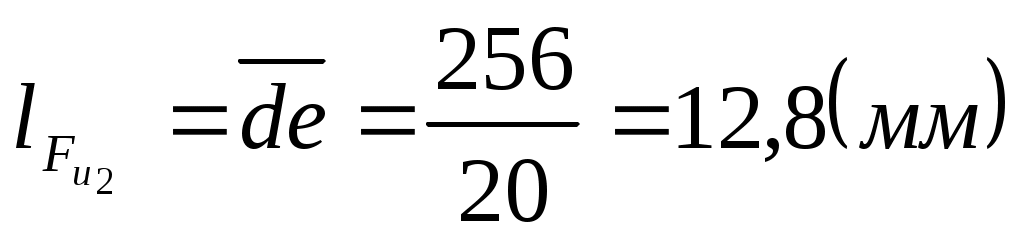 . .
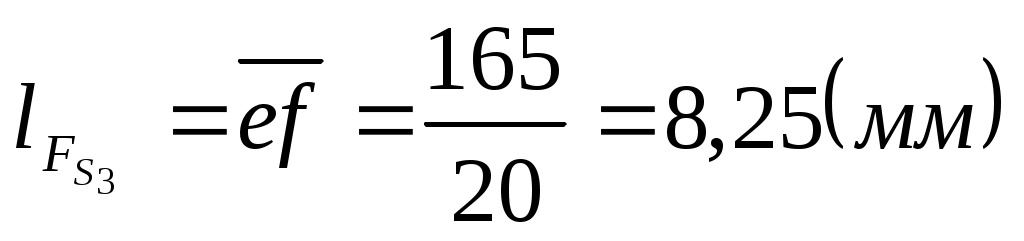 . .
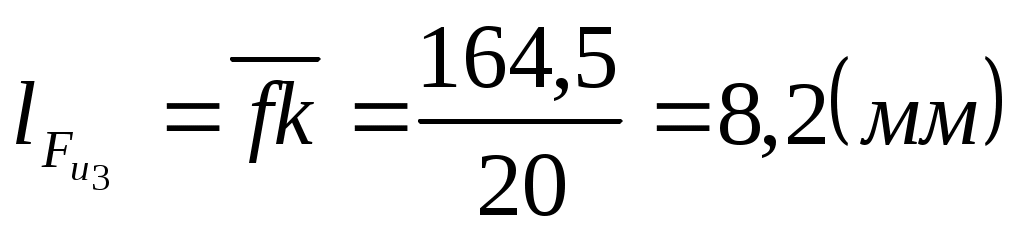 . .
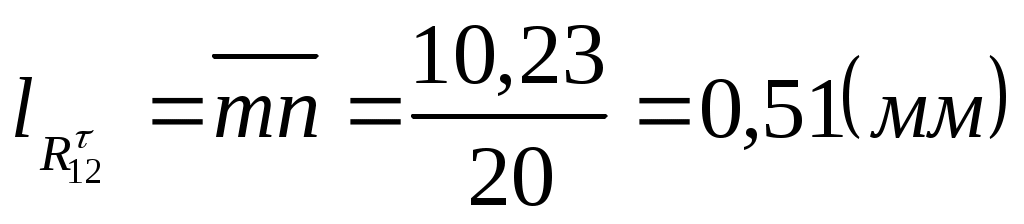
Строим силовой многоугольник, откуда замеряем:
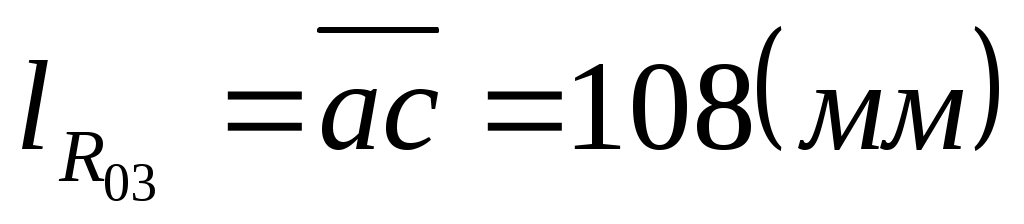 . .
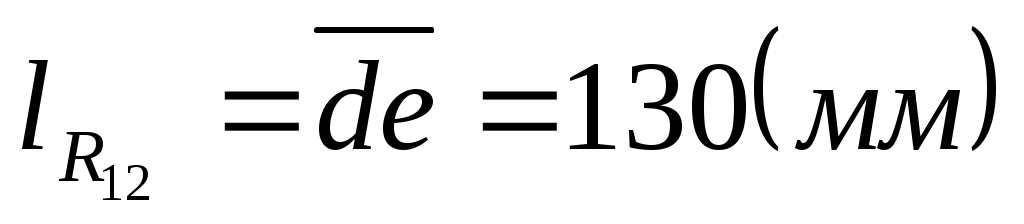 . .
Умножив длины векторов на масштабный коэффициент, определим их модули:
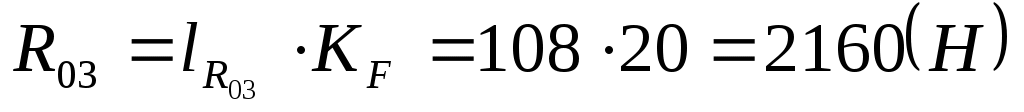 . .
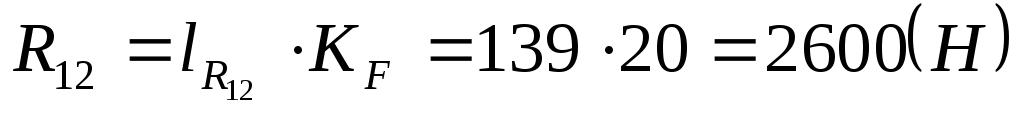 . .
3.3.2 Расчет исходного звена.
На кривошип 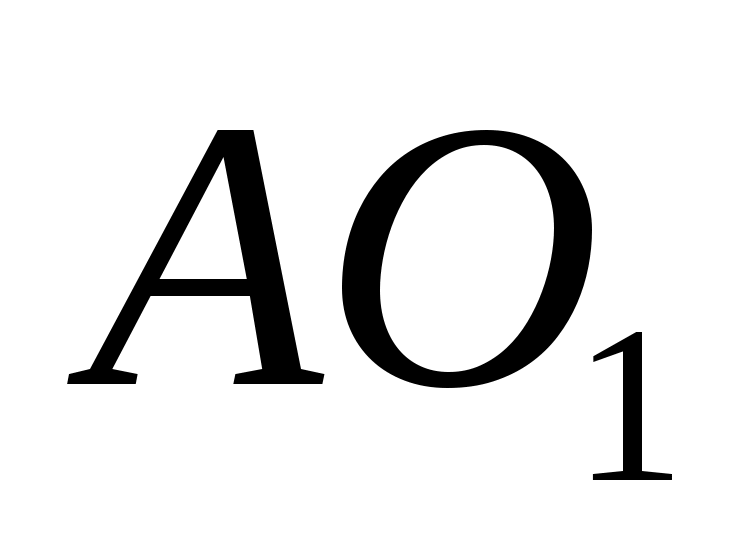 действует сила веса действует сила веса 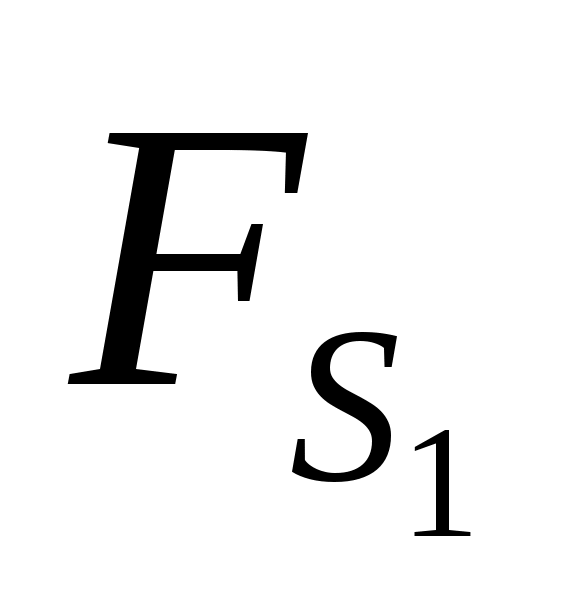 , сила инерции , сила инерции 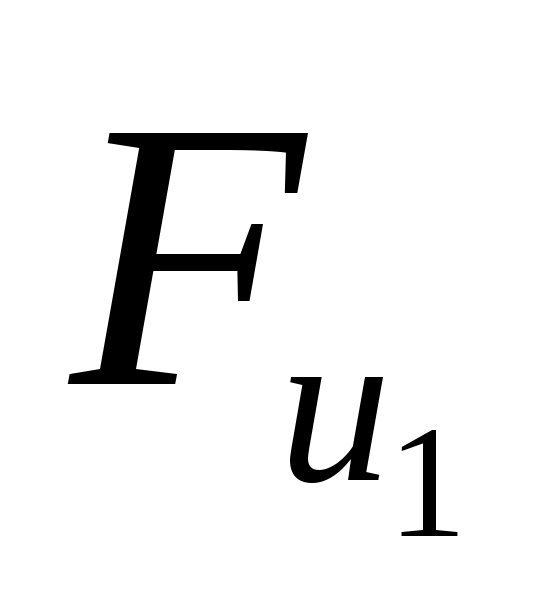 , со стороны звена 2 - реакция , со стороны звена 2 - реакция 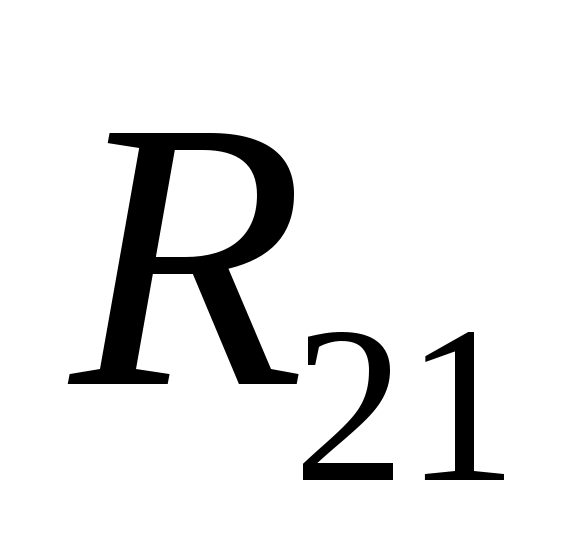 , со стороны стойки - реакция , со стороны стойки - реакция 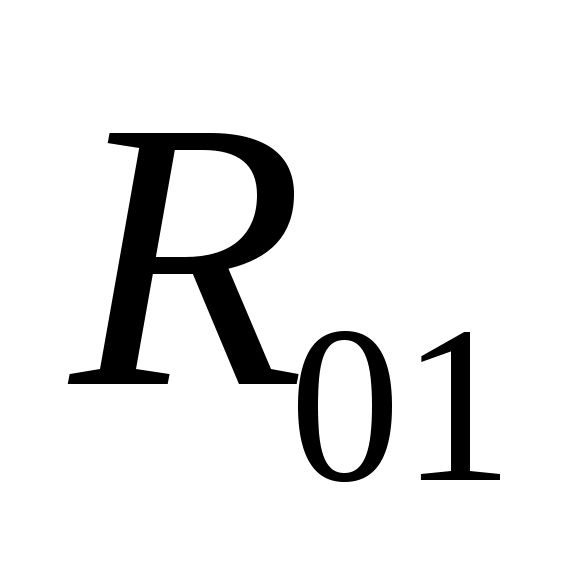 . .

Приложим в точке  искомую уравновешивающую силу искомую уравновешивающую силу 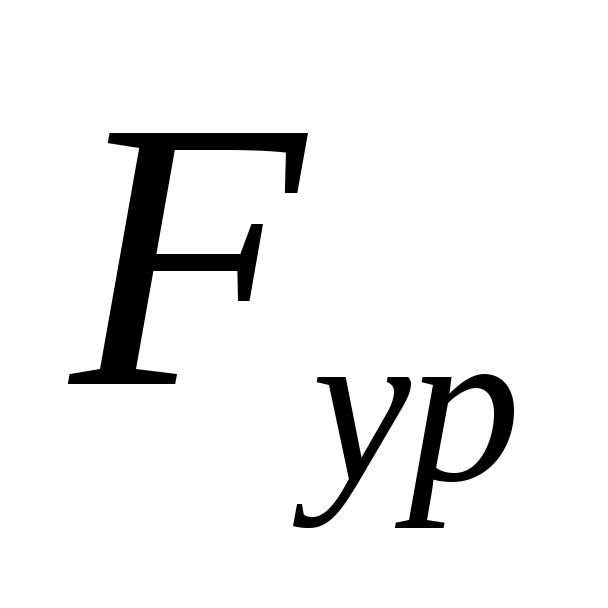 . .
Определяем значение уравновешивающей силы из уравнения моментов относительно точки 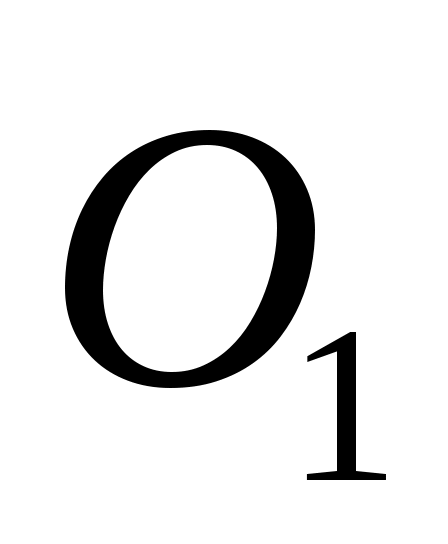 . .
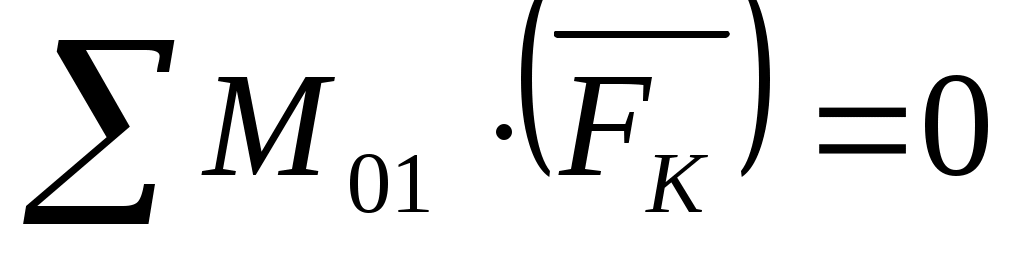 . .
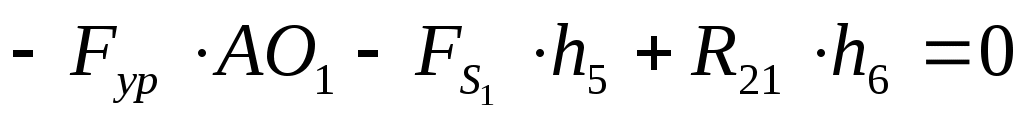 . .
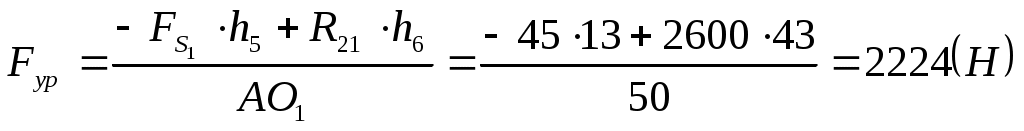 . .
Для определения реакции стойки построим план сил исходного звена:
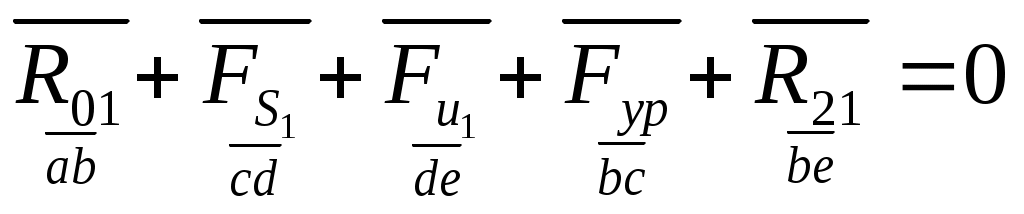 . .
Масштабный коэффициент:
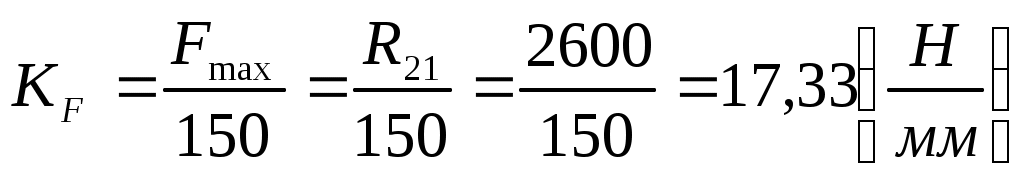 . .
Длины остальных векторов на плане сил.
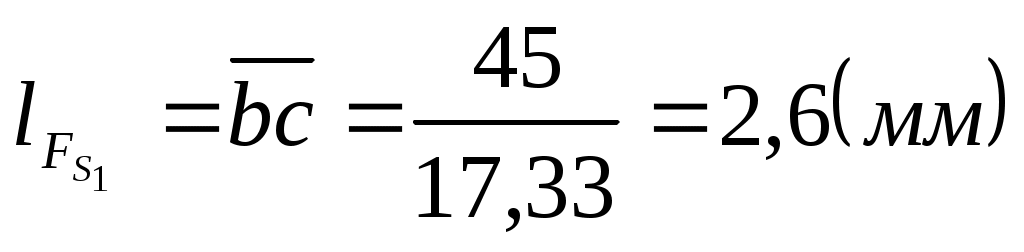 . .
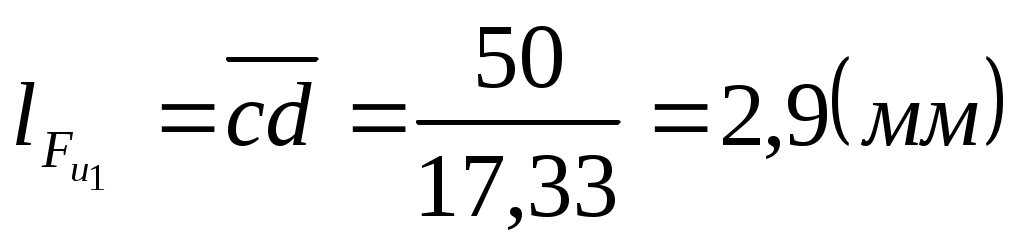 . .
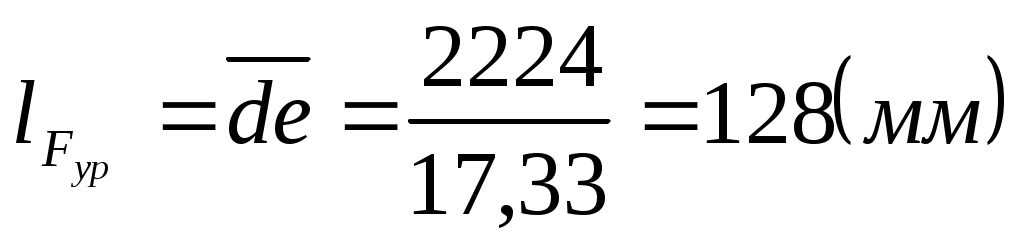 . .
С плана сил замеряем
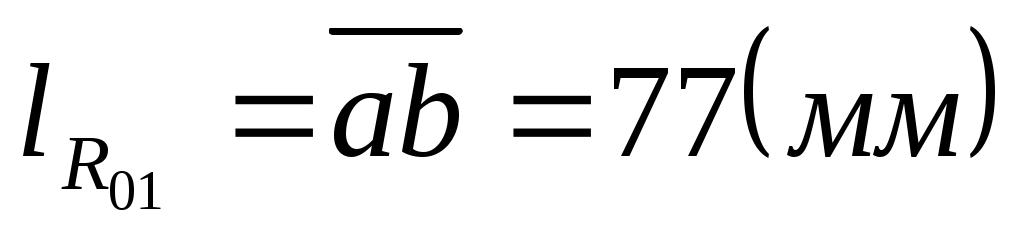 . .
Модуль этой силы равен:
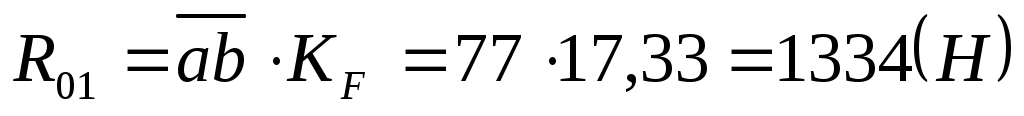 . .
3.5 Определение уравновешивающей силы.
Строим повернутый на  план скоростей механизма (рычаг Жуковского), переносим на него соответствующие точки всех внешних сил, кроме силы план скоростей механизма (рычаг Жуковского), переносим на него соответствующие точки всех внешних сил, кроме силы  приложенной к неподвижной точке приложенной к неподвижной точке 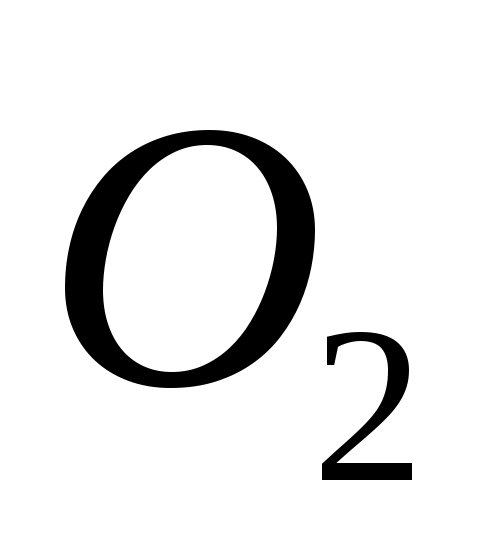 , совпадающей с полюсом , совпадающей с полюсом 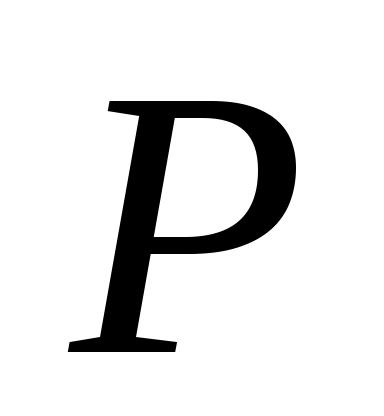 . .

Уравнение равновесия:
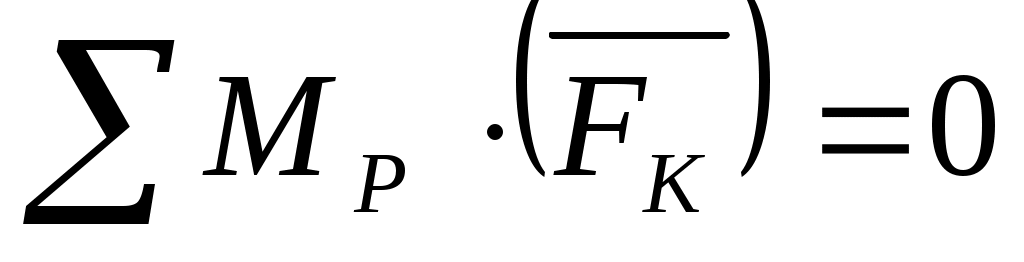 . .
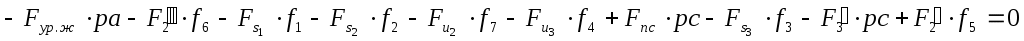
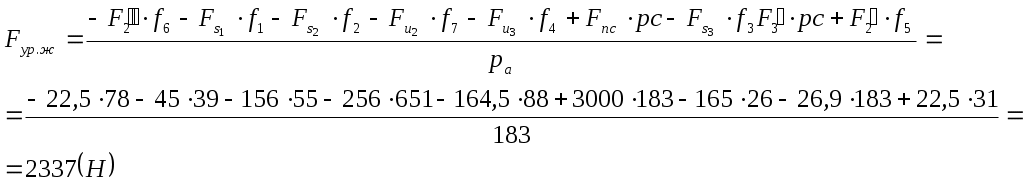
Отклонение от результата силового расчета составляет:
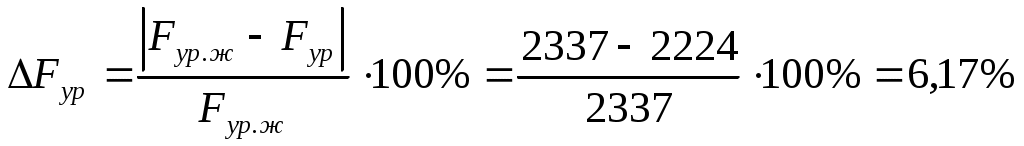
Полученное отклонение в пределах допустимых 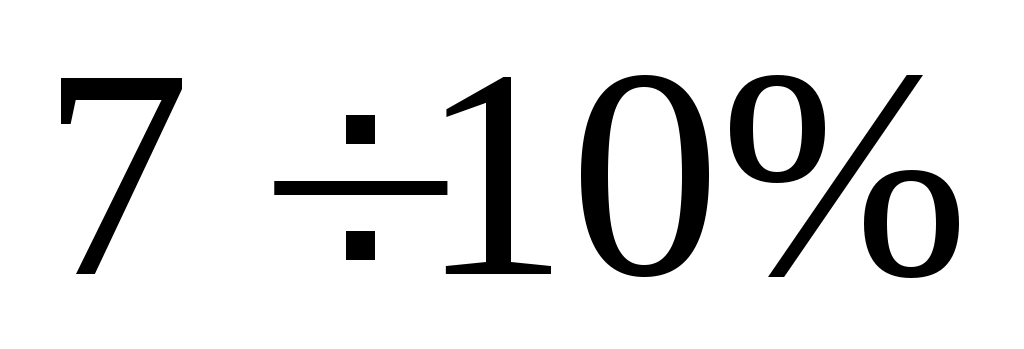 , следовательно силовой расчет выполнен правильно. , следовательно силовой расчет выполнен правильно.

Заключение
Используя графические и расчетно-графические методы анализа курса ТММ, определены скорости, ускорения, силы инерции звеньев механизма, давления в кинематических парах. Определены параметры нулевого зацепления зубчатых колес.
По результатам расчетов выполнен чертеж зубчатого зацепления, построены диаграммы относительного скольжения, с помощью которых исследовано влияние скоростей скольжения на качество работы передачи. Определены теоретическое и действительное значения коэффициента перекрытия, установлена зависимость его от угла зацепления и модуля передачи.
Результаты проектирования можно использовать для создания опытного образца механизма.

Список использованных источников.
1. Артоболевский И.И. Теория механизмов и машин, М.: Наука. 1988. 640 с.
2. Курсовое проектирование по теории механизмов и машин: Учебное пособие для вузов /А.С. Кореняко. Л.И. Кременштейн, С.Д. Петровский и др. Киев: Высшая школа. 1980. 332 с.
3. Бородин А.В. Механизмы малогабаритных поршневых машин с сухим трением. М.: Агат, 1994. 148 с.
4. Структурный, кинематический и силовой анализ механизма. Синтез зубчатой передачи: Методические указания к выполнению контрольной работы и курсового проекта по дисциплине "Теория механизмов и машин". /Н.В. Ковалева, А.В. Бородин. Омский гос. ун-т путей сообщения. Омск. 2000. 48 с.
5. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин. /Под ред. К. В. Фролова. М.: Высшая школа. 2002. 450 с. |
|
|
 Скачать 1.65 Mb.
Скачать 1.65 Mb.


 Введение
Введение 1. Структурный анализ механизма
1. Структурный анализ механизма




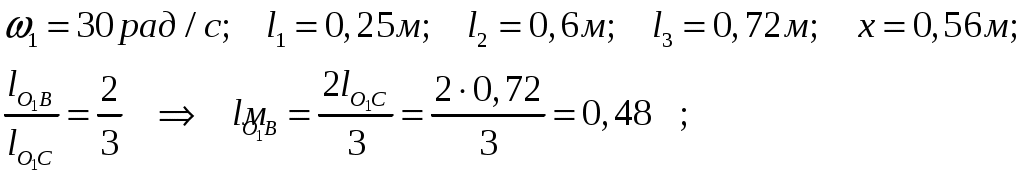



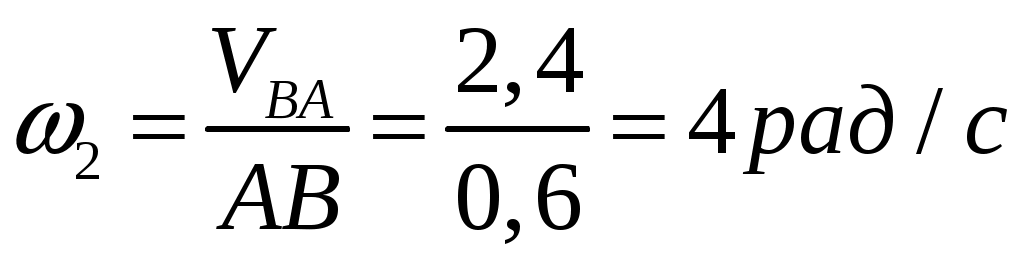 ;
;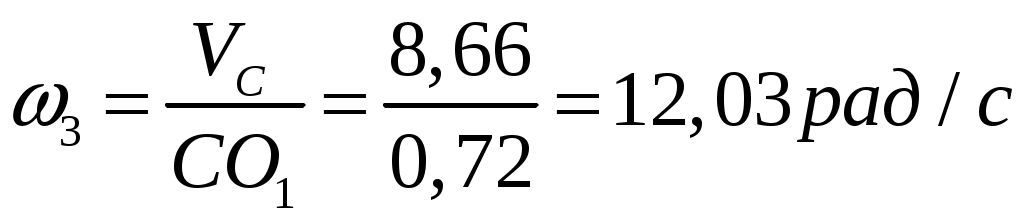 ;
;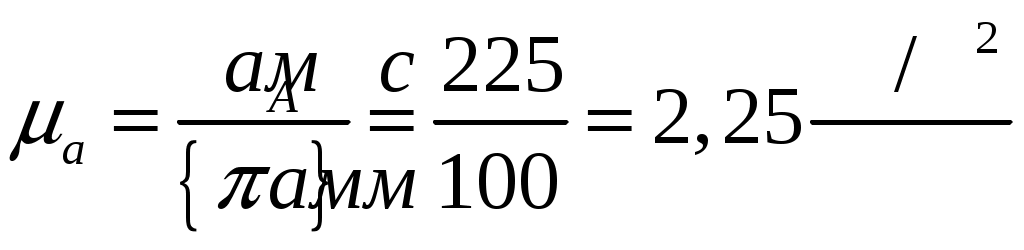 .
. Ускорение точки
Ускорение точки 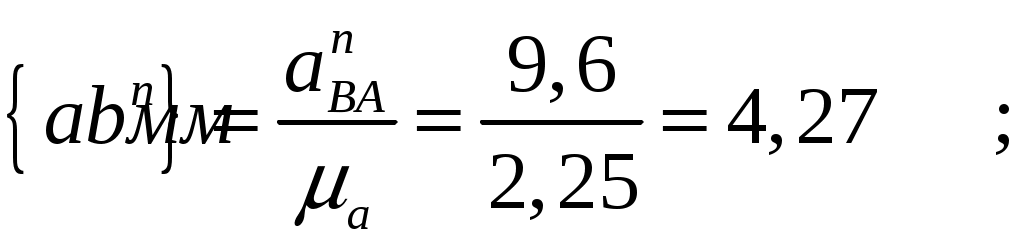
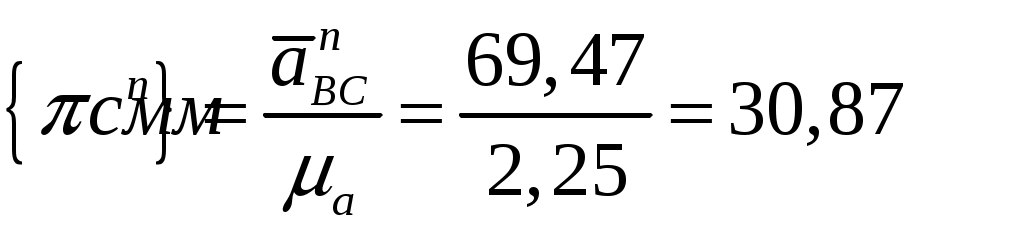 .
.
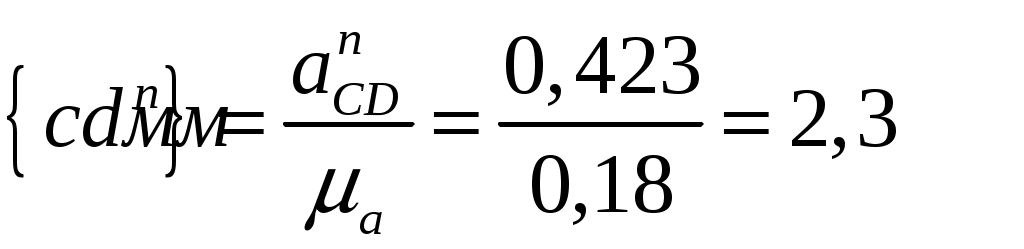 ,
, Используя принцип подобия строим на плане скорости центров масс звеньев. Центры масс расположены на серединах звеньев, значит и на плане скоростей они будут расположены на серединах отрезков, соответствующих звеньям.
Используя принцип подобия строим на плане скорости центров масс звеньев. Центры масс расположены на серединах звеньев, значит и на плане скоростей они будут расположены на серединах отрезков, соответствующих звеньям.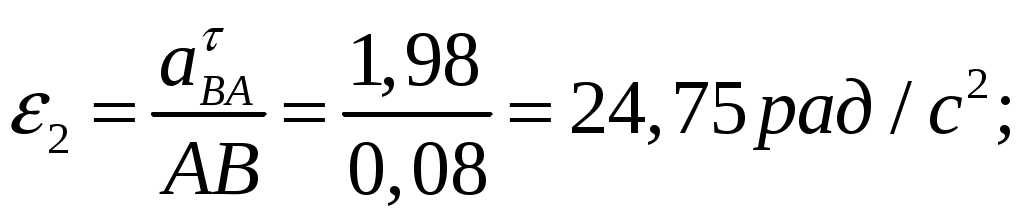
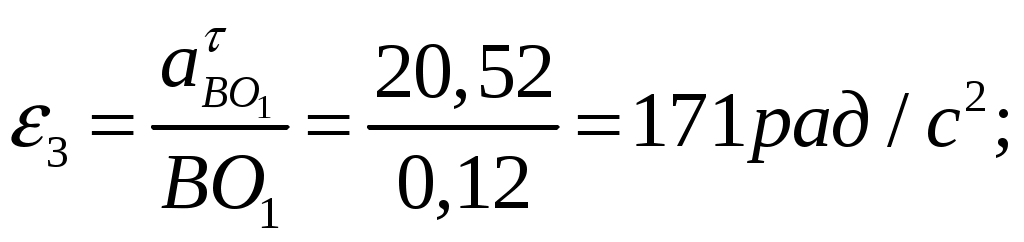
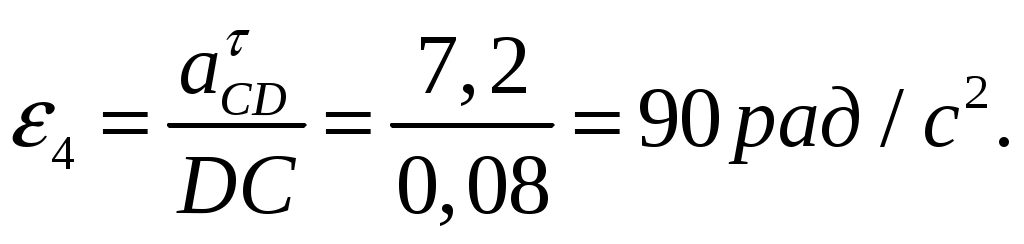




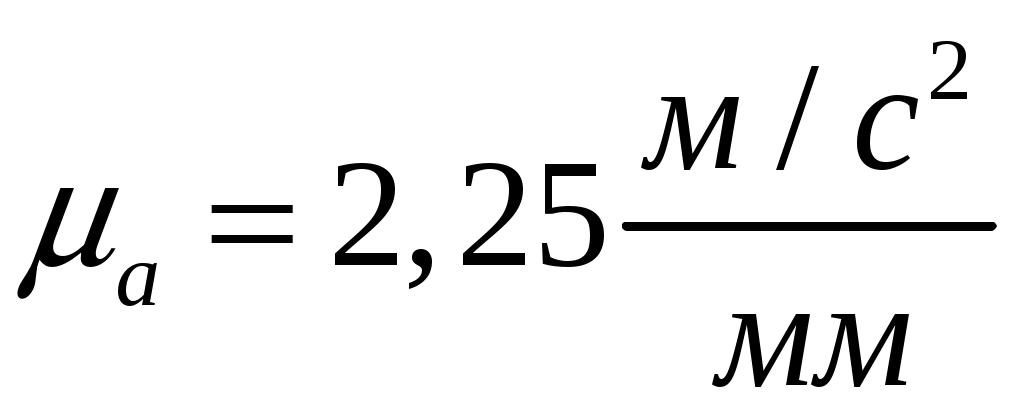




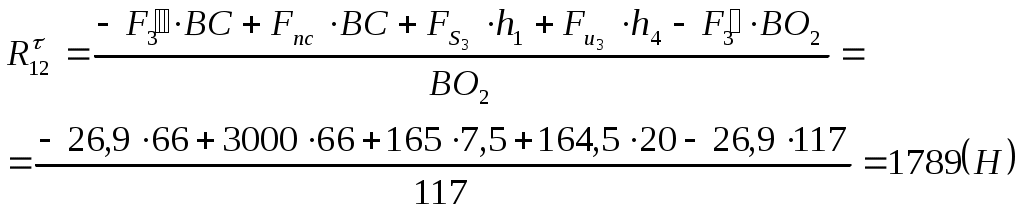 .
.