сопромат. 192114_б-КТОПипу-21_2022_7. Контрольная работа По дисциплине Сопротивление материалов
 Скачать 157.4 Kb. Скачать 157.4 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное образовательное учреждение высшего образования «Саратовский государственный технический университет имени Гагарина Ю.А.» Кафедра: «Техническая механика и мехатроника» (ТММ) Контрольная работа По дисциплине «Сопротивление материалов» Выполнил студент группы: б-КТОПипу-21 Баюков Д.А. Проверил: Ст. ПреподавательКаф. ТММ: Пименов Д.А. Саратов 2022 СОДЕРЖАНИЕ ЛИСТ ЗАДАНИЯ………………………………………………………………...3 1. ПОЛОЖЕНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ…………………………………………………………………….4 2. СТАТИЧЕСКАЯ ОПРЕДЕЛИМОСТЬ КОНСТРУКЦИИ……………………………………………………………...…5 3. РАСЧЁТ СТАТИЧЕСКОГО, ОСЕВОГО МОМЕНТА, МОМЕНТА СОПРОТИВЛЕНИЯ СЕЧЕНИЯ. ЦЕНТР ТЯЖЕСТИ……………………..6 4. УРАВНЕНИЯ СТАТИКИ И ОПОРНЫЕ РЕАКЦИИ……………………………………………………………………...…7 5. КОРРЕКТИРОВКА ПОПЕРЕЧНОГО СЕЧЕНИЯ БАЛКИ…………………………………………………………………………...10 6. КОРРЕКТИРОВКА ПОДОБРАННОГО СЕЧЕНИЯ БАЛКИ………………………………………………………………………...…11 7. ЗАКЛЮЧЕНИЕ ПО РАБОТЕ…………………………………………………………………..……...15 СПИСОК ЛИТЕРАТУРЫ…………………………………………………………...…….16 ЛИСТ ЗАДАНИЯ. Индивидуальное задание выбиралось исходя из задания на расчёт балочной конструкции и номер зачётной книжки студента. Шифр зачётной книжки: 200777
Согласно шифру номера зачетной книжки примем следующие значения:
Для расчета однопролетной статически определимой конструкции перекрытия одноэтажного здания необходимо: 1. Задать положение декартовой системы координат. 2. Рассмотреть статическую определимость конструкции. 3. Рассчитать статический момент, осевой момент, момент сопротивления сечения. Определить центр тяжести сечения. 4. Составить уравнения статики и определить опорные реакции. 5. Из условия прочности скорректировать поперечное сечение балки. 6. Из условия устойчивости скорректировать подобранное поперечное сечение балки. 7. Сделать заключение по работе. ПОЛОЖЕНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ; Выбор декартовой системы координат крайне важен, при расчете изгибаемых элементов конструкции. В первом приближении решения логичнее и правильнее принять начало прямоугольной декартовой системы координат в точке, известной по своим координатам в пространстве расчета. Так как предлагаемое сечение конструкции прямоугольное, то для начала примем начало прямоугольной декартовой системы координат в левом нижнем углу прямоугольного поперечного сечения балки. 55мм 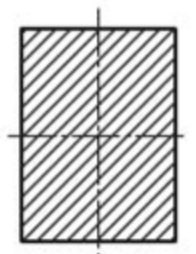   Х Y 55мм Рис.1Начальная точка системы координат После того, как будут определены основные геометрические характеристики прямоугольного поперечного сечения балки, прямоугольную декартовую систему координат необходимо будет совместить с центром тяжести представленного поперечного сечения с целью уменьшения расчетных характеристик и получении более верного оценочного суждения жесткостных параметров. 2. СТАТИЧЕСКАЯ ОПРЕДЕЛИМОСТЬ КОНСТРУКЦИИ; Степень статической неопределимости системы W, определяемую внешними связями, можно по следующей формуле: W = 3 D − 2 Ш − С, гдеD − число частей (“дисков”) системы, каждая из которых может рассматриваться как абсолютно жесткое тело, Ш − количество шарниров в системе, соединяющих эти “диски”, С − число опорных стержней (шарнирно-подвижная связь). 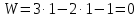 Если W=0 – то система статически определимая 3. РАСЧЕТ СТАТИЧЕСКОГО, ОСЕВОГО МОМЕНТА, МОМЕНТА СОПРОТИВЛЕНИЯ СЕЧЕНИЯ. ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ СЕЧЕНИЯ; Момент сопротивления нетто рассматриваемого поперечного сечения 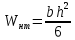 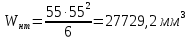 Момент инерции брутто рассматриваемого поперечного сечения 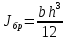 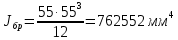 Статический момент инерции брутто рассматриваемого поперечного сечения 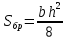 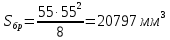 4. УРАВНЕНИЯ СТАТИКИ И ОПОРНЫЕ РЕАКЦИИ; Снеговые нагрузки рассчитываются по СП 20.13330* Нормативное значение снеговой нагрузки на горизонтальную проекцию покрытия следует определять по формуле: S0=CeCtµSg где Ce– коэффициент, учитывающий снос снега с покрытий зданий под действием ветра или иных факторов, принимаемый в соответствии с 10.5-10.9 СП 20.13330; Ct– термический коэффициент, принимаемый в соответствии с 10.10 СП 20.13330; µ – коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие, принимаемый в соответствии с 10.4 СП 20.13330; Sg – нормативное значение веса снегового покрова на 1 м2 горизонтальной поверхности земли, принимаемое в соответствии с 10.2 (см. таблицу 1 ниже). Расчетное значение снеговой нагрузки определяют умножением нормативного значения на коэффициент надежности по снеговой нагрузке: S=S0γf Коэффициент надежности по снеговой нагрузке γf = 1,5. Для III снегового района Sg=1,5кПа. Тогда S0=1111,5=1,5кПа S=1,51,5=2,25кПа Расчетная снеговая нагрузка 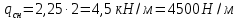 Расчетная нагрузка от собственного веса 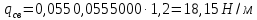 Расчетные сосредоточенные нагрузки 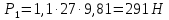 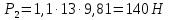 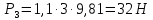 Определение опорных реакций 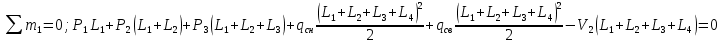 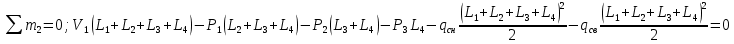 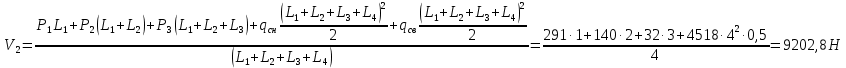 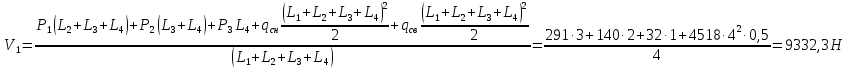 Проверка 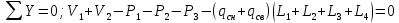 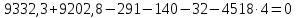 – реакции верны – реакции верныПостроение эпюр М и Q 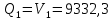 Н Н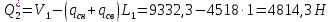 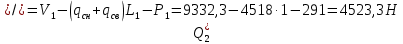 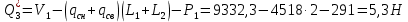 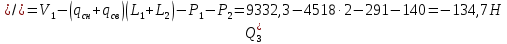 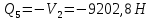 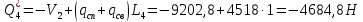 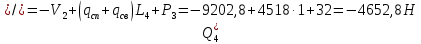 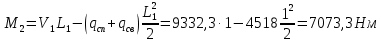 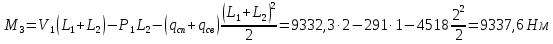 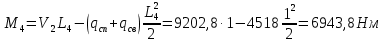 5. КОРРЕКТИРОВКА ПОПЕРЕЧНОГО СЕЧЕНИЯ БАЛКИ; Расчет изгибаемых элементов на прочность производится по формуле: 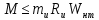 Где 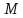 - расчетный изгибающий момент; - расчетный изгибающий момент;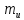 - коэффициент условий работы элемента на изгиб; - коэффициент условий работы элемента на изгиб;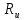 - расчетное сопротивление древесины изгибу; - расчетное сопротивление древесины изгибу;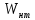 - момент сопротивления нетто рассматриваемого поперечного сечения; - момент сопротивления нетто рассматриваемого поперечного сечения;1·104∙105∙ 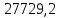 ∙10-9=288,4Нм<9337,6Нм ∙10-9=288,4Нм<9337,6НмУсловие прочности не выполнено Расчет изгибаемых элементов на скалывание древесины производится по формуле: 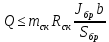 Где 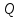 - расчетная поперечная сила; - расчетная поперечная сила;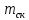 - коэффициент условий работы элемента на скалывание при изгибе; - коэффициент условий работы элемента на скалывание при изгибе;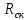 - расчетное сопротивление древесины скалыванию вдоль волокон; - расчетное сопротивление древесины скалыванию вдоль волокон;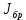 - момент инерции брутто рассматриваемого поперечного сечения; - момент инерции брутто рассматриваемого поперечного сечения;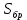 - статический момент инерции брутто сдвигаемой части сечения относительно нейтральной оси; - статический момент инерции брутто сдвигаемой части сечения относительно нейтральной оси;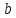 – ширина сечения; – ширина сечения;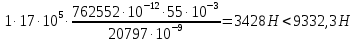 Условие прочности не выполнено Требуемый момент сопротивления сечения 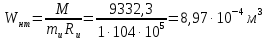 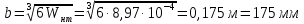 6. КОРРЕКТИРОВКА ПОДОБРАННОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ БАЛКИ; Перед тем, как корректировать поперечное сечение из условия устойчивости по второй группе предельных состояний, необходимо скорректировать некоторые геометрические характеристики балки. Соответственно, получим: 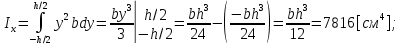 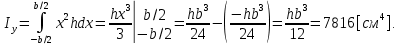 Жесткостной параметр для определения устойчивости по второй группе предельных состояний в совокупности найденных параметров будет определен следующим образом: 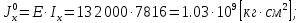 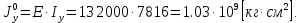 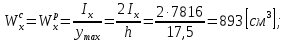 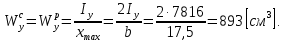 Для определения значений углов перемещений и линейных вертикальных перемещений, воспользуемся методом начальных параметров. Данный метод позволит исследовать балочную конструкцию секционно и описать функционально каждую из них. Так как метод начальных параметров завязан на начальных параметрах угла поворота конструкции и линейного перемещения в начальной точке, то определим их. Прямоугольную декартову систему координат расположим на левой опоре конструкции, так как показано на рисунке 4. Так как левая опора является шарнирно неподвижной, то начальное перемещение в ней будет отсутствовать. Начальный угол поворота будет определен и условия функции на правом краю конструкции, где также известно перемещение. Тогда воспользуемся рекуррентной формулой и получим следующее значение начального угла поворота: 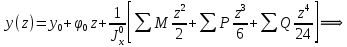 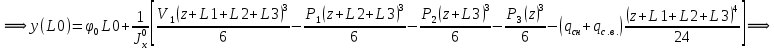 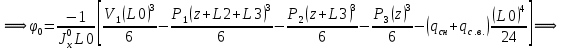 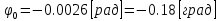 Участок №1. Это участок при параметре L1. Переменная z будет изменять в пределах значения от нуля до параметра L1. Уравнение начального параметра примет вид: линейные перемещения примут следующие значения - 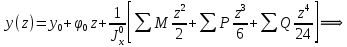 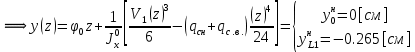 угловые повороты примут следующие значения - 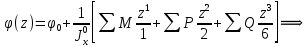 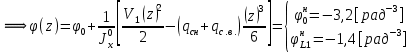 Участок №2. Это участок при параметре L2+L1. Переменная z будет изменять в пределах значения от нуля до параметра L2. Уравнение начального параметра примет вид: линейные перемещения примут следующие значения - 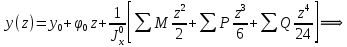 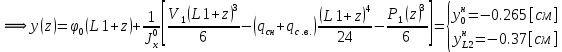 угловые повороты примут следующие значения - 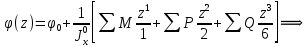 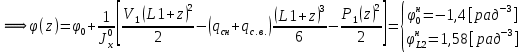 Участок №3. Это участок при параметре L3+L2+L1. Переменная z будет изменять в пределах значения от нуля до параметра L3. Уравнение начального параметра примет вид: линейные перемещения примут следующие значения - 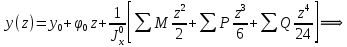 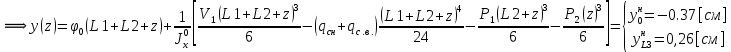 угловые повороты примут следующие значения - 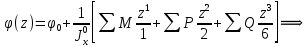 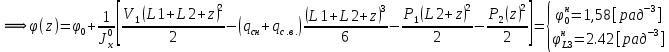 Участок №4. Это участок при параметре L4+L3+L2+L1. Переменная z будет изменять в пределах значения от нуля до параметра L4. Уравнение начального параметра примет вид: линейные перемещения примут следующие значения - 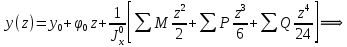 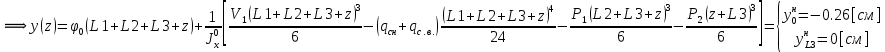 угловые повороты примут следующие значения - 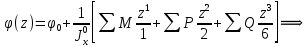 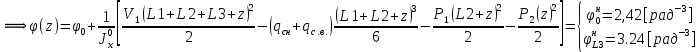 В виде графика получится следующий результат по второй группе предельных состояний:
По результатам расчета выяснилось, что максимально возможные перемещения в центре конструкции не превышают значения допустимые по условию задачи (1.4 см), но все же есть три пути решения оптимизации конструкции. Первое – изменить осевой момент инерции путем увеличения высоты конструкции; второе – изменить осевой момент инерции путем увеличения ширины конструкции; третье – изменение жесткости конструкции путем изменения показателя модуля упругости материала. 7. ЗАКЛЮЧЕНИЕ ПО РАБОТЕ. В работе была проверена прочность заданного сечения балки на изгибную прочность и прочность сечения на скол. Заданные размеры не подходят под нагрузки. Рассчитано новое значение сечения балки.  Рис.2 СПИСОК ЛИТЕРАТУРЫ 1.Сборник задач по сопротивлению материалов : учеб. пособие для вузов / А. В. Александров [и др.] ; ред. А. В. Александров. - Москва :Стройиздат, 1977. - 336 с. 2.Избранные задачи и вопросы по сопротивлению материалов : учеб. пособие / В. И. Феодосьев. - 3-е изд., испр. и доп. - Москва : Наука, 1967. - 376 с. 3.Расчет и нормирование надежности строительных конструкций / В. Д. Райзер ; ред. И. Я. Драчевская. - Москва :Стройиздат, 1995. - 352 с. 4.Сборник задач по сопротивлению материалов: Учеб. пособие для вузов / Н. М. Беляев, Л. К. Паршин, Б. Е. Мельников и др.; под ред. Л. К. Паршина. - СПб. : Изд-во "Иван Федоров", 2003. - 432 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
