контрольная работа по методике преподавания математики в начальной школе. кр. р. Курлыкина Л. М. дИПОНб-18-1. Контрольная работа по дисциплине теоретические основы преподавания математики в начальной школе студент гр дИпонб181 по направлению подготовки бакалавриата 44. 03. 01
 Скачать 296.62 Kb. Скачать 296.62 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Магнитогорский государственный технический университет им. Г. И. Носова» Институт заочного обучения Кафедра педагогического образования и документоведения КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ Теоретические основы преподавания математики в начальной школе Выполнил: студент гр. дИПОНб-18-1 по направлению подготовки бакалавриата 44.03.01 «Педагогическое образование» профиль «Начальное образования» Курлыкина Людмила Михайловна Магнитогорск 2020-2021 учебный год ТЕМА: Положительные рациональные числа 1. Докажите, что а) число 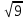 ; ;б) число log 10; в) число 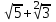 является рациональным или иррациональным. Решение: а) число является числом рациональным, т.к.  = 3, проверка = 3, проверка 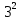 = 9. = 9. б) число log 10; допустим, что это число является иррациональным. Тогда существуют такие взаимно простые числа pиq, 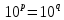 , или р = q; р и q натуральные числа, значит, число log 10, является рациональным числом. , или р = q; р и q натуральные числа, значит, число log 10, является рациональным числом.в) число 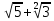 иррациональное. Обозначим это число через иррациональное. Обозначим это число через  , , 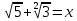 , возведём обе части уравнения в квадрат, получим , возведём обе части уравнения в квадрат, получим 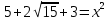 , т.е. , т.е. 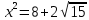 .Итак, данное число является иррациональным. .Итак, данное число является иррациональным.2. Докажите равносильность дробей: 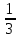 и и  . .Решение: Приведение дробей к общему знаменателю, есть замена их равносильными дробями, имеющими одинаковые знаменатели. Наименьший знаменатель данных дробей, есть наименьшее общее кратное K(3; 15). Найдем его, представив числа 3 и 15 в каноническом виде. Получим: K (3; 15) = 15 Так как 15 = 3 * 5 = 15 * 1 , то 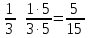 и и 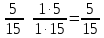 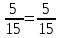 – эти дроби равны, а значит равносильны. – эти дроби равны, а значит равносильны.3.Приведите к наименьшему общему знаменателю дроби 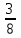 и и 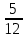 . .Решение: Приведение дробей к общему знаменателю есть замена их равносильными дробями, имеющими одинаковые знаменатели. Наименьший знаменатель данных дробей есть наименьшее общее кратное K(8; 12). Найдем его, представив числа 8 и 12 в каноническом виде. Получим: K (8; 12) = 24 Так как 24 = 8*3 = 12*2, то 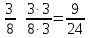 и и 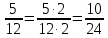 Ответ: 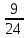 и и  4. Как короче записать сумму 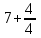 . .Решение: 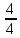 = 1, значит 7 + 1 = 8 = 1, значит 7 + 1 = 85. Сложите дроби 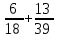 . .Решение: Для того чтобы найти сумму дробей, для начала нужно привести обе дроби к общему знаменателю. Наименьший знаменатель данных дробей, есть наименьшее общее кратное К (18; 39). Найдем его, представив числа 18 и 39 в каноническом виде. Получим: К (18;39) = 234 Так как 234 = 18 * 13 = 39 * 6, то  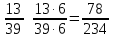 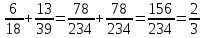 6. Найдите произведение:  . .Решение:  7. Выполните деление: 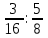 . .Решение: 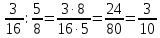 8. Сравните числа 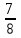 и и  . .Решение: Для того чтобы сравнить два действительных числа, достаточно найти разность этих чисел и сравнит ее с нулем. Если разность будет положительна, то первое число (уменьшаемое разности) будет больше второго числа (вычитаемого разности); если же разность будет отрицательна, то наоборот. Для сравнения этих чисел составим и вычислим их разность  Для вычисления разности приводим данные к общему знаменателю. В данном случае общий знаменатель равен 16. После этого используя правило вычитания дробей с одинаковыми знаменателями вычитаем из числителя первой дроби числитель второй дроби, а знаменатель оставляем прежним. Теперь обратим внимание, что разность этих чисел получилась положительной, следовательно, первое число (уменьшаемое) больше второго (вычитаемого), т.е 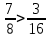 9. Какие из дробей можно записать в виде конечной десятичной дроби?  . .Решение: 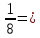 1 : 8 = 0,125 – конечная десятичная дробь. 1 : 8 = 0,125 – конечная десятичная дробь.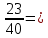 23 : 8 =0,575 – конечная десятичная дробь. 23 : 8 =0,575 – конечная десятичная дробь.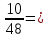 10 : 48 =0,208(3) – смешанная периодическая дробь. 10 : 48 =0,208(3) – смешанная периодическая дробь.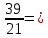 39 : 21 =1,(857142) – чисто периодическая дробь. 39 : 21 =1,(857142) – чисто периодическая дробь.10. Докажите, что бесконечная десятичная дробь числа Пи 3.14159265358979323…. (4 миллиона знаков числа Пи. Интересный факт: любая последовательность цифр числа пи рано или поздно найдется.) представляет собой иррациональное число. ТЕМА: Положительные действительные числа Запишите десятичные приближения иррационального числа π = 3,1415… по недостатку и по избытку с точностью до: а) 0,1; б) 0,01; в) 0,001. Решение: а) 3,1415 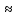 3,1 3,1б) 3,1415 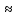 3,14 3,14в) 3,1415 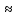 3,142 3,142Найдите десятичные приближения с точностью до 0,1 по недостатку и по избытку для чисел: 4,3885,  . .Решение: 4,3885 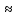 4,3 – с недостатком. 4,3 – с недостатком.4,3885 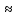 4,4 – с избытком. 4,4 – с избытком.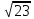 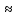 4,79583152 4,79583152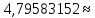 4,7 – с недостатком. 4,7 – с недостатком.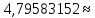 4,8 – с избытком. 4,8 – с избытком.Найдите первые три десятичных знака суммы 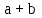 , если: , если:а) а = 2,34871…, b = 5,63724…; б) 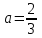 , b = π; , b = π;в)  ; ; 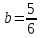 ; ;г)  ; ; 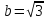 . .Решение: Возьмем десятичные приближения слагаемых с четырьмя десятичными знаками: а) 2,3487 + 5,6372 = 7,9859 Ответ: 7,986 б) 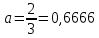 b = π = 3,1415 0,6666 + 3,1415 = 3,8081 Ответ: 3,809 в) a = 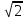 = 1,4142 = 1,4142b = 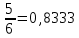 1,4142 + 0,8333 = 2,2475 Ответ: 2,248 г) a = 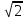 = 1,4142 = 1,4142b = 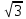 = 1,7320 = 1,73201,4142 + 1,7320 = 3,1462 Ответ: 3,146 Найдите два первых десятичных знака произведения 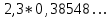 . .Решение: 2,3 * 0,38548 = 0,88 Найдите два первых десятичных знака произведения a * b, если: а) a = 1,703504…, b = 2,04537...; б) а = 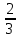 , ,  ; ; в)  ; ; 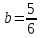 ; ; г)  ; ; 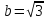 . .Решение: а) Берем десятичные приближения данных чисел с тремя десятичными знаками: 1,703 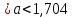 и и 2,045  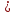 2,046. По определению произведения чисел с тремя десятичными знаками: 2,046. По определению произведения чисел с тремя десятичными знаками:1,703*2,045 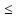 a*b a*b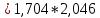 или 3,483 или 3,483 a*b a*b 3,486. 3,486.Таким образом, a*b = 3,48… б) 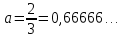 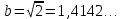 Берем десятичные приближения данных чисел с тремя десятичными знаками: 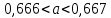 и и 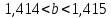 . По определению произведения чисел с тремя десятичными знаками: . По определению произведения чисел с тремя десятичными знаками: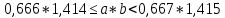 или или 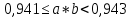 Таким образом, 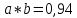 … …в) 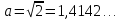 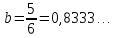 Берем десятичные приближения данных чисел с тремя десятичными знаками: 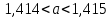 и и 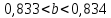 . По определению произведения чисел с тремя десятичными знаками: . По определению произведения чисел с тремя десятичными знаками: или или 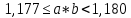 Таким образом, 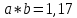 … …г) 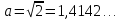 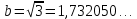 Берем десятичные приближения данных чисел с тремя десятичными знаками: 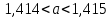 и и 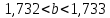 . По определению произведения чисел с тремя десятичными знаками: . По определению произведения чисел с тремя десятичными знаками: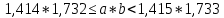 или или 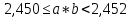 Таким образом, 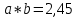 … …Вычислите результат с точностью до сотых 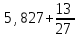 , ,  . .Решение: Преобразуем дробь  в десятичную дробь, и вычислим в десятичную дробь, и вычислим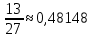 5,827+0,48148 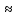 6,31 6,31Преобразуем дробь 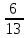 в десятичную дробь, и вычислим в десятичную дробь, и вычислим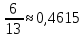 7,806 – 0,4615 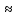 7,34 7,34Вычислите значение выражения с точностью до 0,001: 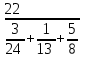 . .Решение:  ТЕМА: Действительные числа Используя переместительный и сочетательный законы, вычислите значение выражения наиболее рациональным способом: а) б) в) Решение: а) 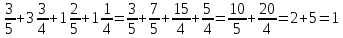 б) 5,3+4,25-2,3+0,75=5,3-2,3+4,25+0,75=3+5=8 в) 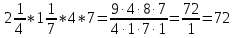 Выполните действие: а) 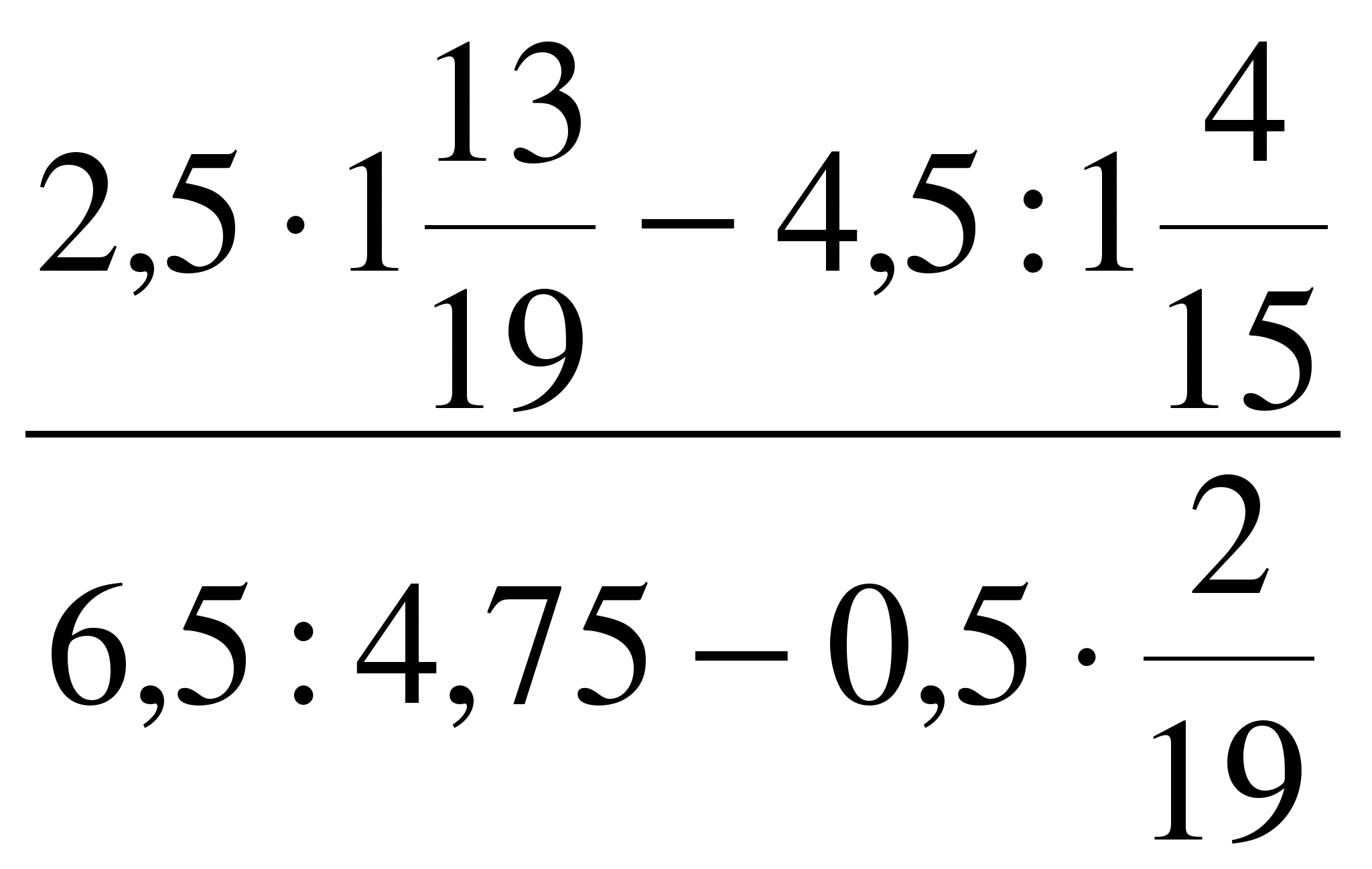 б)  . . Решение: а) 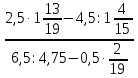 1) 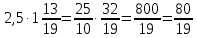 2) 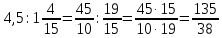 3)  4) 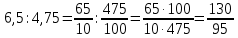 5)  6) 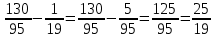 7) 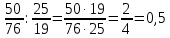 Ответ: 0,5 б)  1) 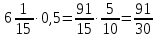 2) 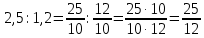 3) 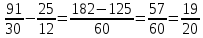 4) 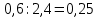 5) 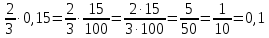 6) 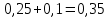 7) 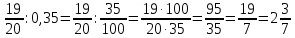 Ответ: 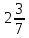 Найдите значение выражения: 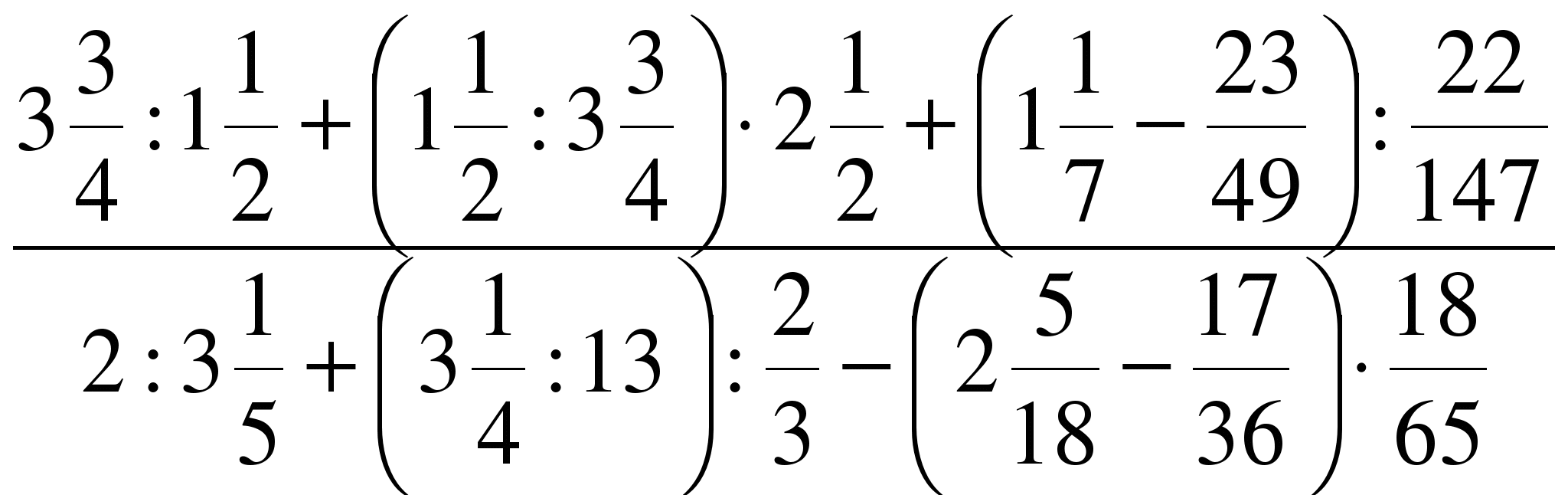 . .Решение: Выполним вычисление по действиям: 1 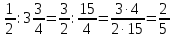 ; ; 1 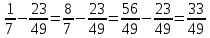 ; ; 3 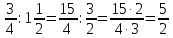 ; ;  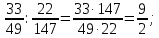 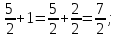  ; ; ; ;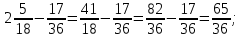 2:3  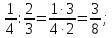 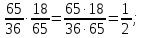 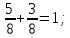 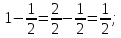 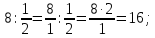 Ответ: 16 Упростите выражение: 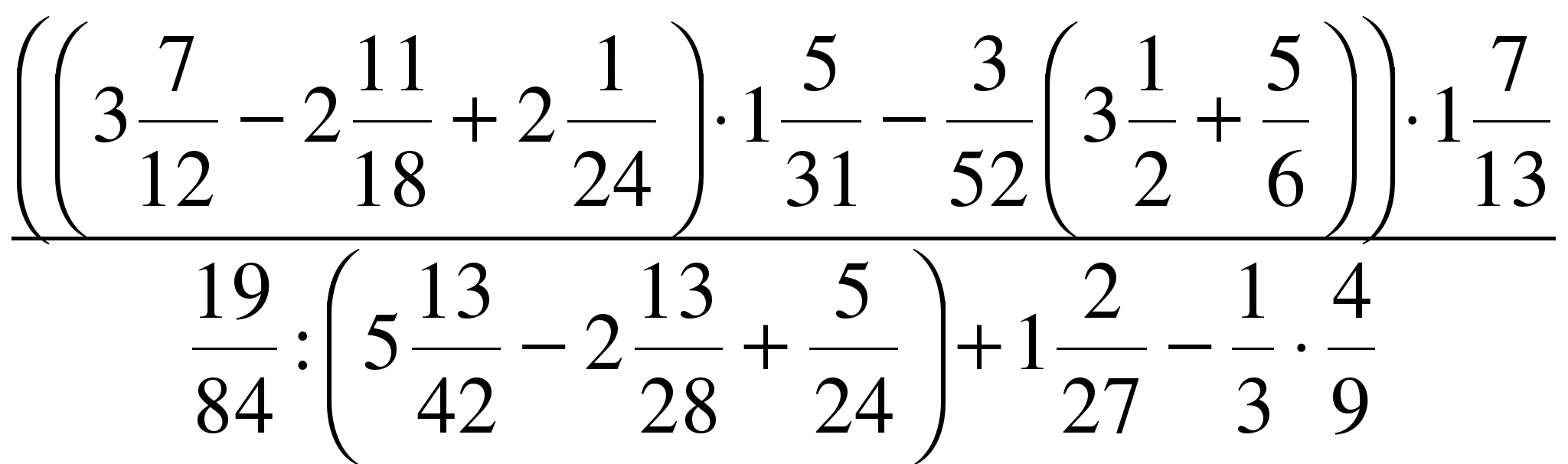 Решение:  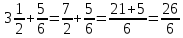 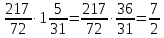  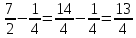 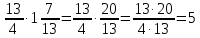  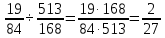 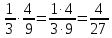 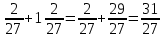 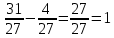 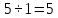 Ответ: 5 |
