КОНТРОЛЬНАЯ РАБОТА по дисциплине Теория автоматического управления 1. Репнин вар 15. Контрольная работа по дисциплине "Теория автоматического управления 1"
 Скачать 296 Kb. Скачать 296 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет» Кафедра Микропроцессорных средств автоматизации КОНТРОЛЬНАЯ РАБОТА по дисциплине "Теория автоматического управления 1" Вариант № 15
Пермь 2020 г. Содержание Исходные данные ………………………………………………….....…3 Анализ устойчивости по корням характеристического уравнения……...…………………………………………………………..4 Анализ устойчивости по критерию Гурвица.............................................5 Анализ устойчивости по критерию Михайлова ……………………..….5 Анализ устойчивости по критерию Найквиста ………………..…….….7 Построение асимптотической ЛАЧХ ……………………...…….………9 Определение показателей качества корневым методом………………..11 Описание исходной системы методом пространства состояния ……………………...………………………………………………………12 Список литературы…………………………………………...…………..15 Исходные данные Передаточная функция разомкнутой части системы имеет вид: 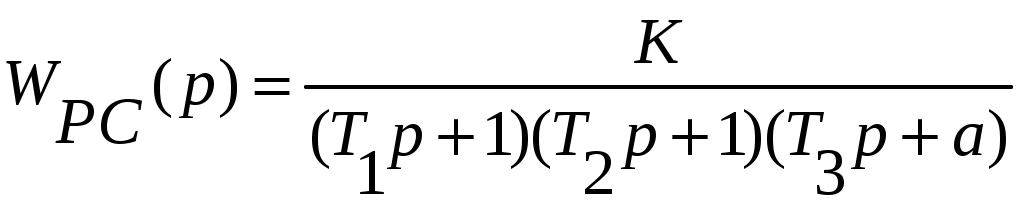 Численные значения параметров:
Задание Подтвердить устойчивость следующими методами: по корням характеристического уравнения; по критерию Гурвица; по критерию Михайлова; по критерию Найквиста По передаточной функции РАЗОМКНУТОЙ системы построить ЛАЧХ. (с учетом масштабов – на миллиметровой бумаге или в Visio) Определить основные показатели качества САУ косвенным (корневым) методом Построить схему переменных состояния ЗАМКНУТОЙ САУ методом последовательного программирования и определить основные матрицы: матрицу входа, матрицу выхода, матрицу коэффициентов, матрицу обхода Подтвердить устойчивость следующими методами: по корням характеристического уравнения Передаточная функция разомкнутого контура системы: Передаточная функция замкнутой системы с единичной обратной связью (по правилам структурных преобразований): 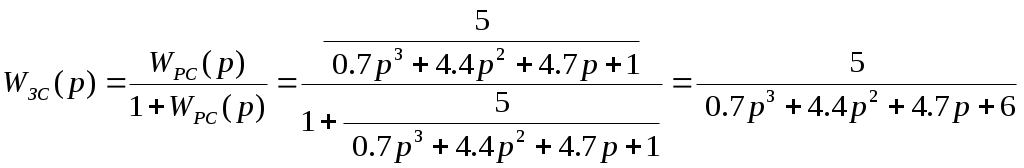 Характеристическое уравнение Определим корни характеристического уравнения замкнутой САУ. Значения корней определяем с помощью пакета Matlab (команда roots): >> roots([0.7 4.4 4.7 6]) ans = -5.3274 -0.4792 + 1.1745i -0.4792 - 1.1745i Действительные части всех корней отрицательные, значит, система устойчива. Подтвердить устойчивость САУ по критерию Гурвица Критерий Гурвица: «Для устойчивости замкнутой системы n-го порядка необходимо и достаточно, чтобы при а0>0 были положительными все n определителей, составленных из коэффициентов характеристического уравнения системы» При порядке системы n=3 (частный случай критерия) для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля, и произведение средних коэффициентов было больше произведения крайних (определитель Для исследуемой САУ все коэффициенты характеристического уравнения больше нуля. Определитель Исследуемая система устойчива. Подтвердить устойчивость САУ по критерию Михайлова Для определения устойчивости по критерию Михайлова следует получить действительную – Затем следует построить кривую Михайлова, откладывая Формулировка критерия Михайлова: автоматическая система управления, описываемая уравнением п-го порядка, устойчива, если при изменении от 0 до характеристический вектор системы Это означает, что характеристическая кривая устойчивой системы должна при изменении от 0 до пройти последовательно через n квадрантов. Строим график (рис. 1) характеристической кривой Михайлова замкнутой САУ, используя пакет Матлаб: >> w=10^(-2):0.01:10^2; >> Re=-4.4*w.^2+6; >> Im=4.7*w-0.7*w.^3; >> plot(Re,Im) >> grid 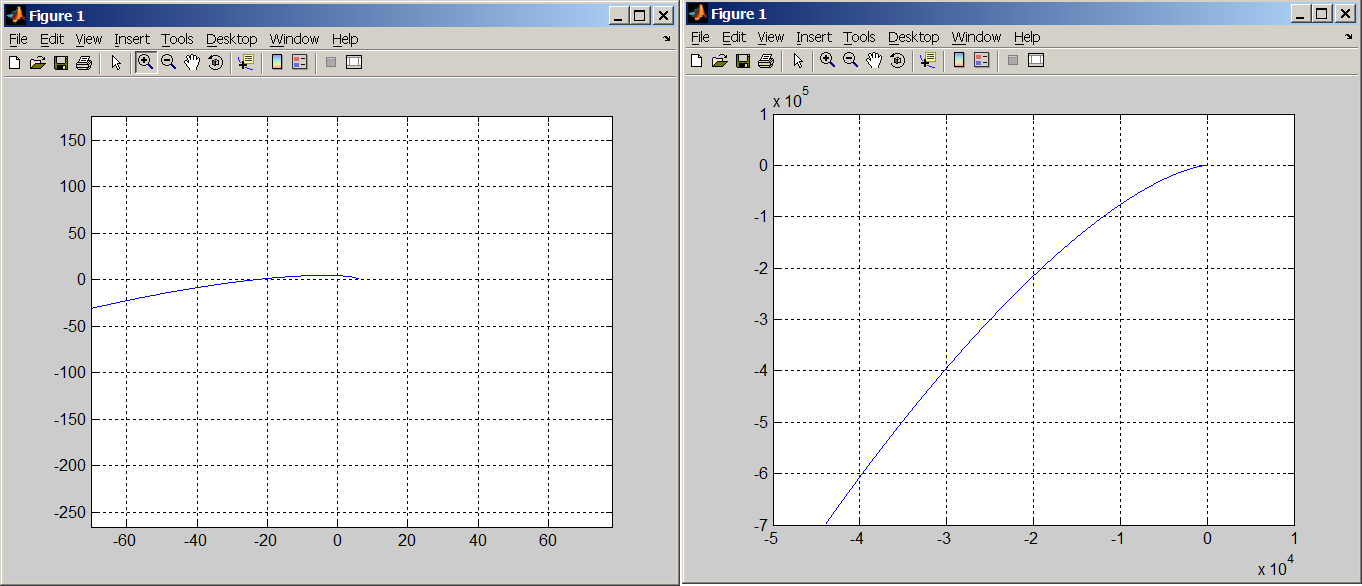 а б Рис. 1 – Годограф Михайлова замкнутой системы автоматического управления (а-начало графика, крупно, б-общий вид) По графику видно, что кривая начинается в первом квадранте, затем переходит во второй, и заканчивается в третьем. Это значит, что система устойчива. Подтвердить устойчивость САУ по критерию Найквиста Критерий Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутого контура системы. Формулировка критерия Найквиста: замкнутая автоматическая система управления устойчива, если разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФЧХ через ось абсцисс слева от точки (-1; ј0) равна m/2, где m — число правых корней характеристического уравнения разомкнутого контура. Определим количество правых корней разомкнутой системы. Характеристическое уравнение разомкнутой системы: Значения корней: 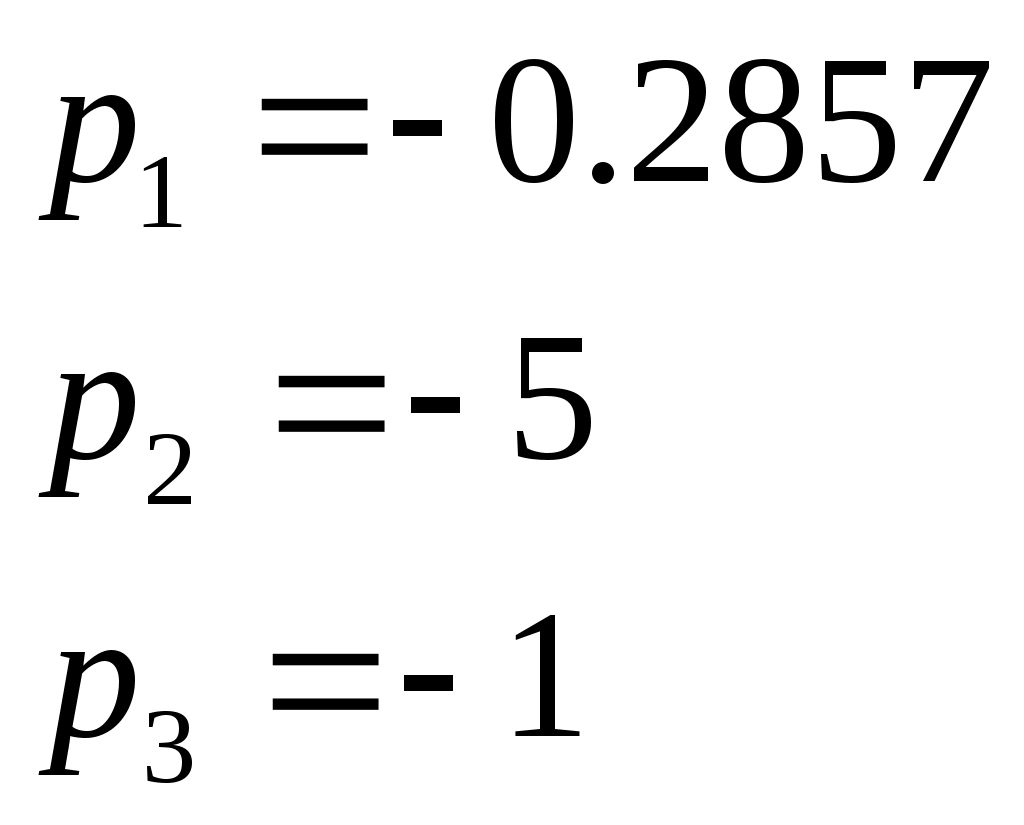 Правых корней нет. Строим график (рис. 2) АФЧХ разомкнутой САУ, используя пакет Матлаб и команду nyquist: >> w=10^(-2):0.01:10^2; >> s=tf('s') Transfer function: s >> W0=5/(0.7*s^3+4.4*s^2+4.7*s+1) Transfer function: 5 ----------------------------- 0.7 s^3 + 4.4 s^2 + 4.7 s + 1 >> nyquist(W0,w) 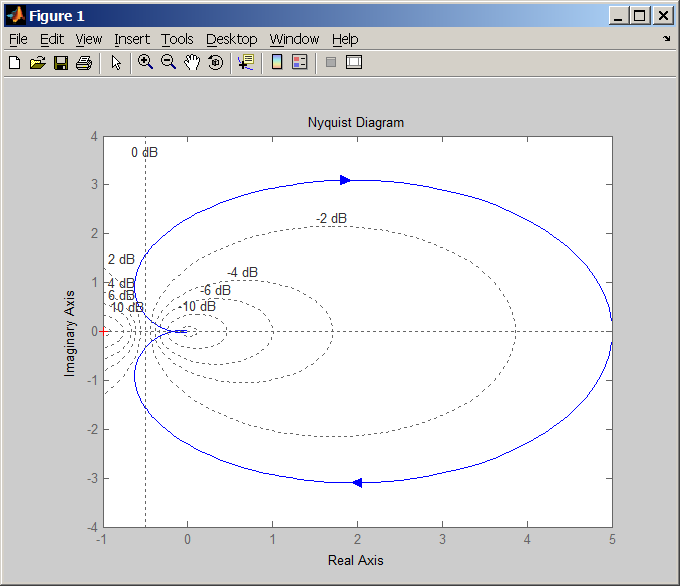 Рис. 2 – График АФЧХ разомкнутой САУ. Полученный график строится для положительных и отрицательных значений частот. Для анализа достаточно рассмотреть график только при положительных частотах. График начинается в первом квадранте и заканчивается в начале координат (нижняя кривая со стрелкой). При устойчивой разомкнутой САУ для устойчивости замкнутой требуется, чтобы АФЧХ разомкнутой не охватывала точку (-1; ј0). Исследуемая замкнутая система устойчива. Построить асимптотическую логарифмическую амплитудно-частотную характеристику (ЛАЧХ) разомкнутой системы. Найдём сопрягающие частоты и соответствующие им логарифмы частот: 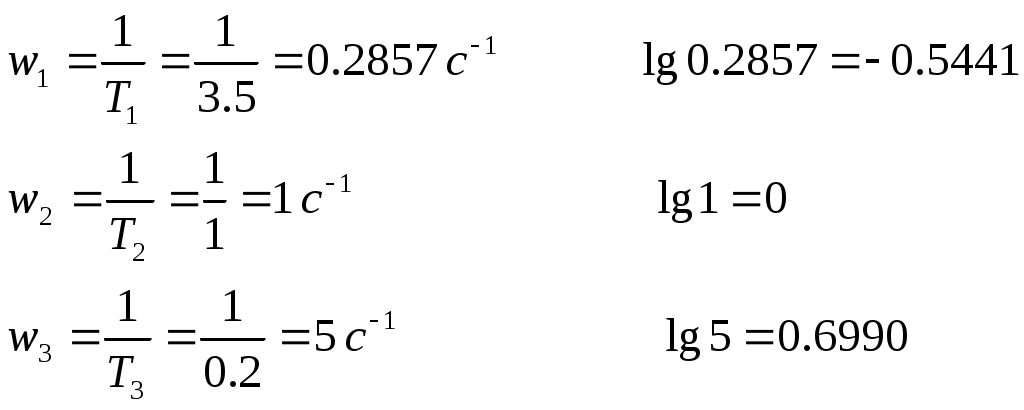 Рассчитаем величину Точка построения первой асимптоты: Степень астатизма Наклон первой асимптоты: Первая асимптота начинается в бесконечности (изображается от оси ординат) и заканчивается на первой сопрягающей частоте. Вторая асимптота (от первой до второй сопрягающей частоты). Наклон второй асимптоты: Третья асимптота (от второй до третьей сопрягающей частоты). Наклон третьей асимптоты : Четвертая асимптота (от третьей сопрягающей частоты до бесконечности). 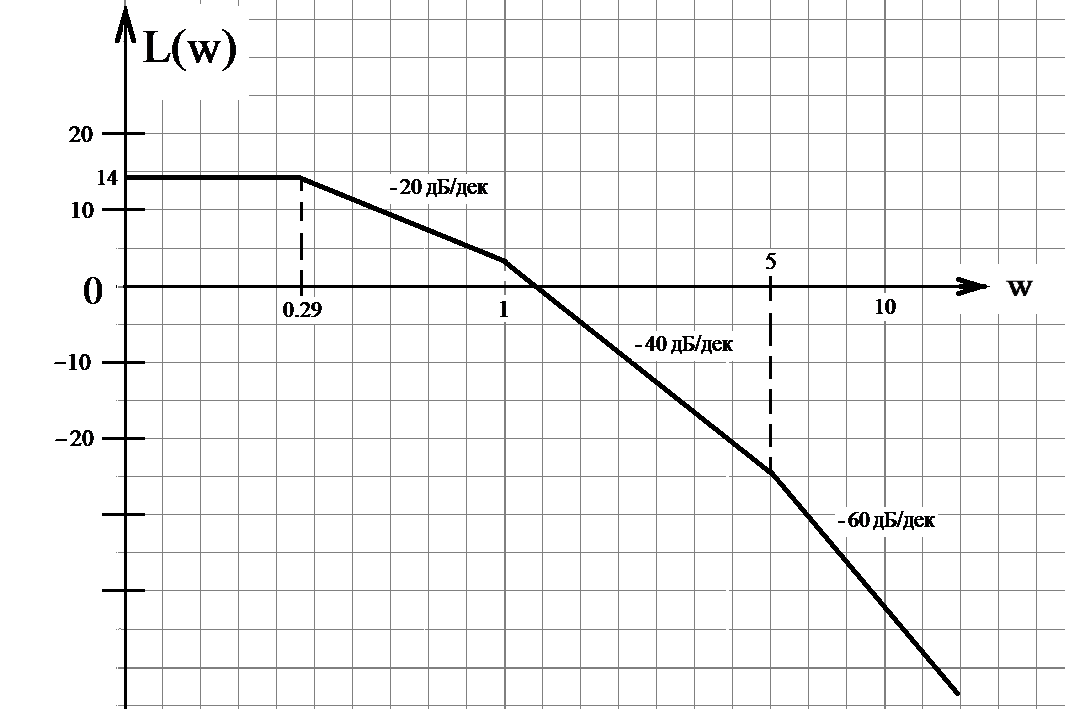 Рис. 3– График асимптотической ЛАЧХ системы автоматического управления. Определить основные показатели качества САУ косвенным (корневым) методом Корни характеристического уравнения замкнутой устойчивой системы: (см. п.1-а). -5.3274 -0.4792 + 1.1745i -0.4792 - 1.1745i Корневые показатели качества. Среднее геометрическое значение модулей корней, характеризует быстродействие САУ. 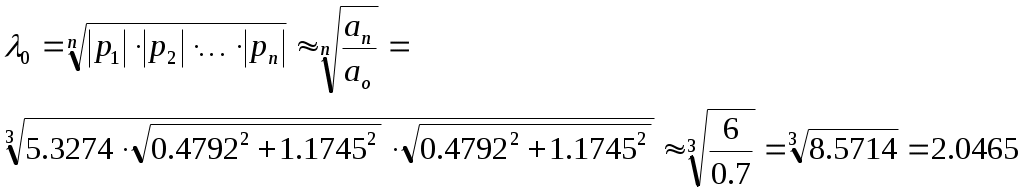 Степень устойчивости – это расстояние от мнимой оси до действительной части ближайшего к ней корня. Степень устойчивости характеризует быстродействие системы и позволяет приблизительно определить ожидаемое время переходного процесса. Степень колебательности характеризует величину перерегулирования и определяется максимальным значением отношения мнимой части к действительной для всех пар комплексных сопряженных корней Корневой показатель колебательности тоже характеризует величину перерегулирования, определяется через доминирующую пару комплексных корней:Оптимальные значения показателя колебательности 0,2-0,5. Так как показатель исследуемой САУ находится внутри указанного интервала, то коэффициент перерегулирования будет не больше 30%. Построить схему переменных состояния ЗАМКНУТОЙ САУ методом последовательного программирования и определить основные матрицы: матрицу входа, матрицу выхода, матрицу коэффициентов, матрицу обхода Преобразуем передаточную функцию системы для построения СПС последовательным программированием: 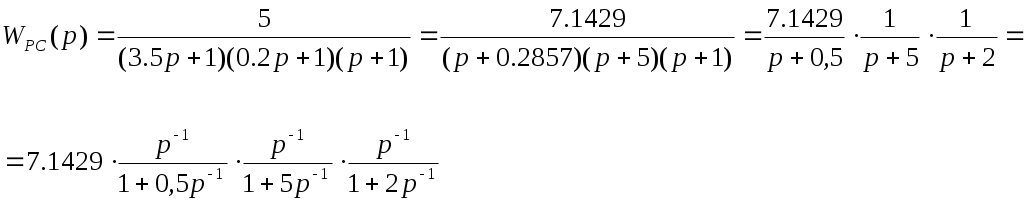 Построим схему переменных состояния, замкнув систему обратной связью: 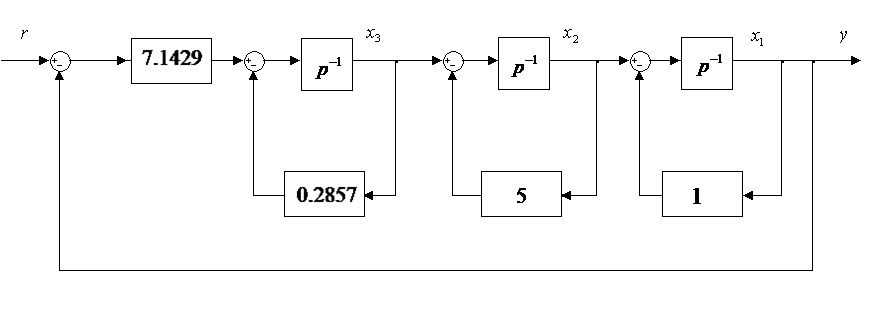 Определим состояние объекта (выберем порядок переменных вектора 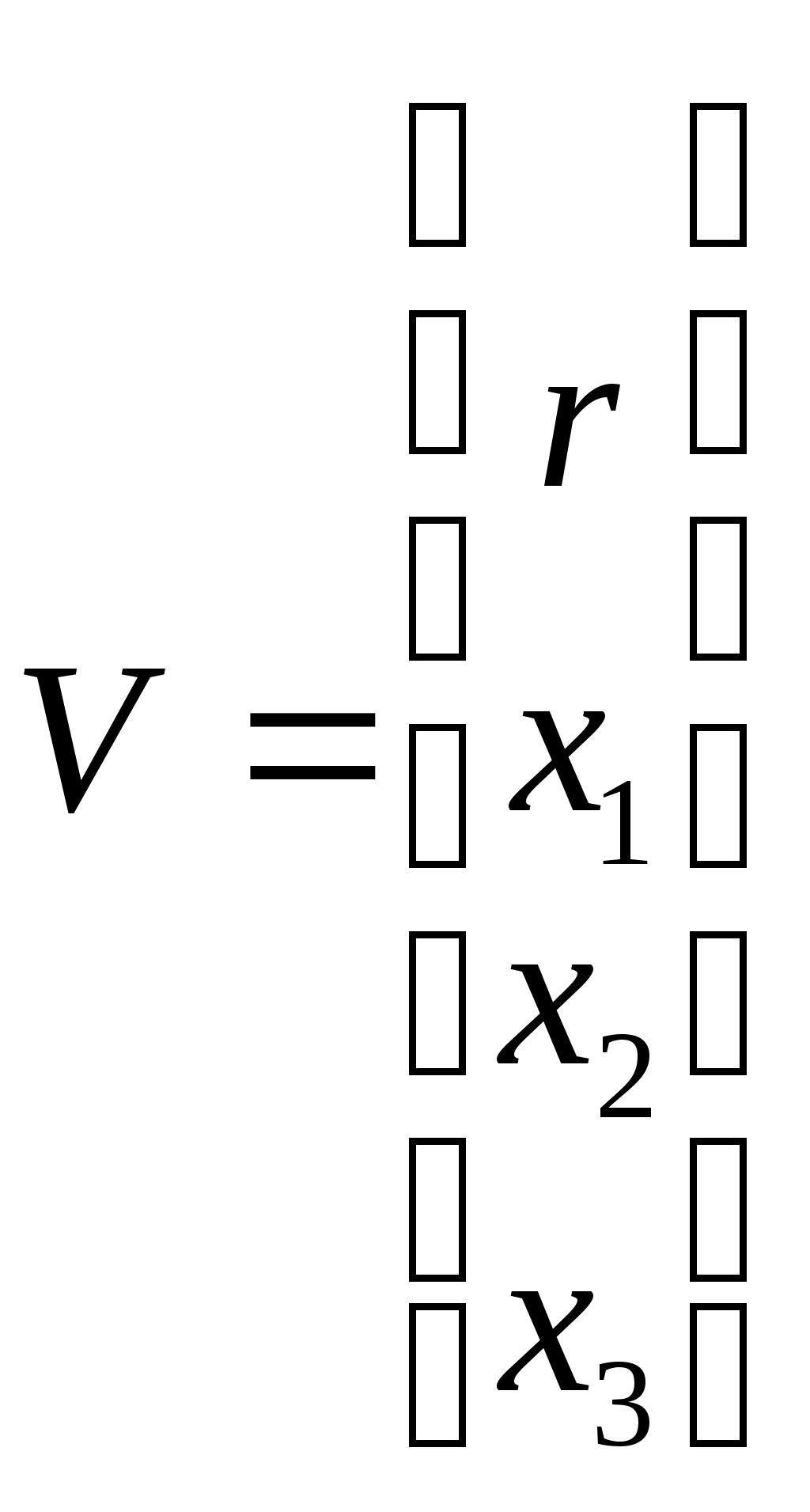 , следовательно: , следовательно: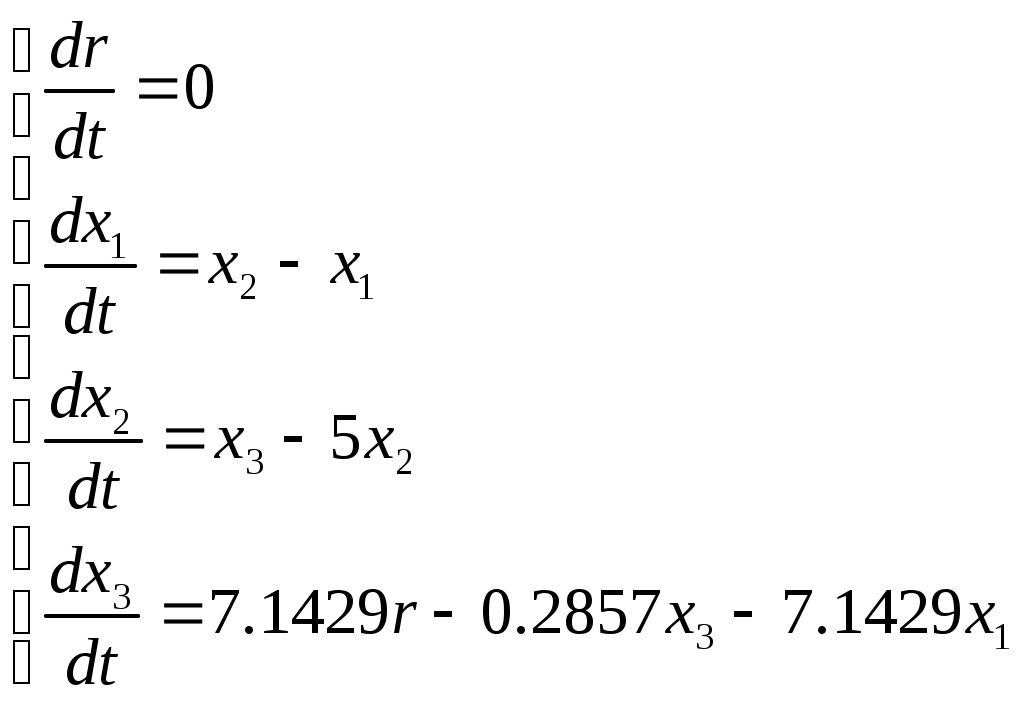 По системе уравнений составляется расширенная матрица состояния 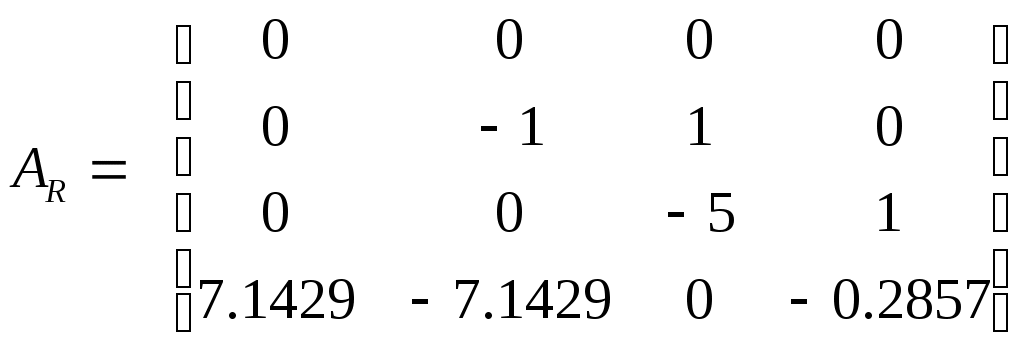 По системе уравнений также можно получить матрицу состояния 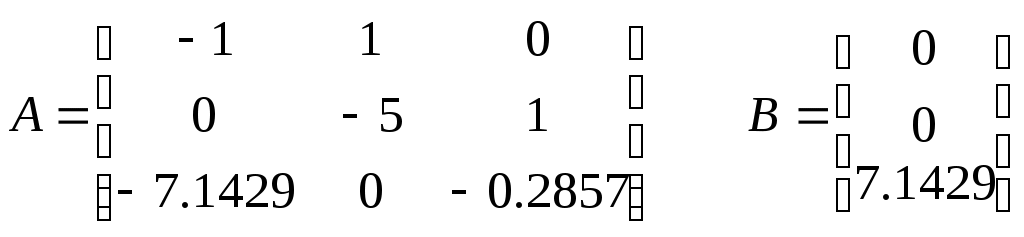 По уравнению выхода: составляются расширенная матрица Список литературы Лукас В.А. Теория управления техническими системами, Екатеринбург, 2005 Бесекерский В.А., Попов Е.П. Теория систем автоматического управления: СПб., 2007 Дорф Р., Бишоп Р. Современные системы управления: М., 2012. |
