Главная страница
Навигация по странице:

  • Контрольная работа по дисциплине «Теория вероятностей»4 семестр Выполнил

  • Группа

  • Ответ

    		•

    теория вероятностей. Теория вероятностей_КР_вар2. Контрольная работа по дисциплине Теория вероятностей 4 семестр Выполнил Фёдоров Иван Николаевич Группа тбт02


    Скачать 77.5 Kb.
    НазваниеКонтрольная работа по дисциплине Теория вероятностей 4 семестр Выполнил Фёдоров Иван Николаевич Группа тбт02
    Анкортеория вероятностей
    Дата26.10.2022
    Размер77.5 Kb.
    Формат файлаdoc
    Имя файлаТеория вероятностей_КР_вар2.doc
    ТипКонтрольная работа
    #755553

    Федеральное государственное бюджетное образовательное учреждение

    высшего образования
    «Сибирский государственный университет телекоммуникаций и информатики»

    Кафедра техносферной безопасности

    Контрольная работа по дисциплине

    «Теория вероятностей»
    4 семестр


    Выполнил: Фёдоров Иван Николаевич

    Группа: ТБТ-02

    Вариант: 2

    Проверила: Храмова Татьяна Викторовна

    Новосибирск, 2022
    Задание 1. Комбинаторика
    Сколько 5-ти буквенных слов можно составить из букв слова

    Х О Д О К ?
    Решение. Переставить буквы в слове можно 5! способами (формула числа перестановок из n элементов: Pn = n!). При этом в слове имеется две одинаковые буквы О. Если менять местами эти буквы в конкретной расстановке, то слова будут получаться одинаковые. Следовательно, общее число слов, составленных перестановкой букв из слова Х О Д О К будет равно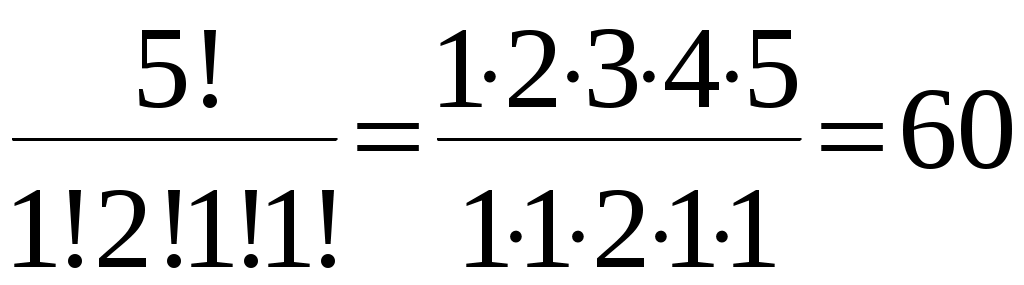


    Ответ: 60 слов.

    Задание 2. Основные теоремы
    Две трети всех сообщений передается по первому каналу связи, остальные - по второму. Вероятность искажения при передаче по первому каналу равна 0,01, по второму - 0,04. Какова вероятность искажения произвольно взятого сообщения?
    Решение.
    Рассмотрим следующие два события:

    Событие A – произвольно взятое сообщение искажено;

    событие B – произвольно взятое сообщение не искажено.
    Выдвинем следующие гипотезы:
    Н1 – сообщение передавалось по первому каналу связи;

    Н2 – сообщение передавалось по второму каналу связи.
    Вероятности гипотез, согласно статистическому определению вероятности, равны: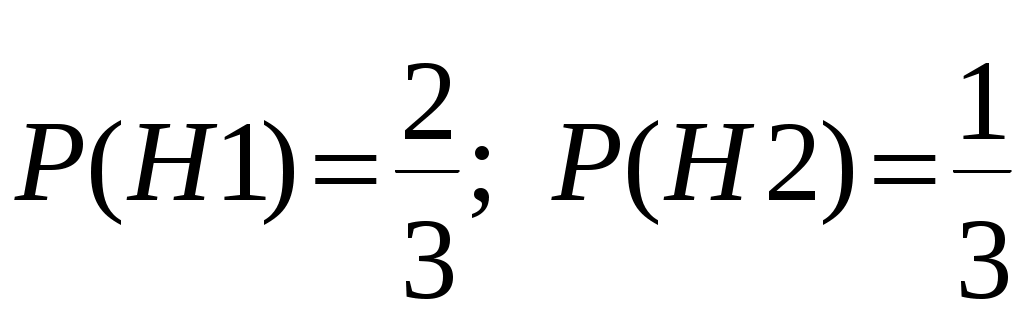

    Условные вероятности события А известны: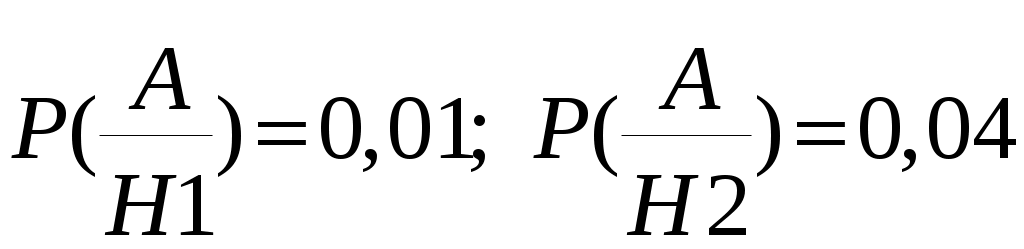


    И по формуле полной вероятности: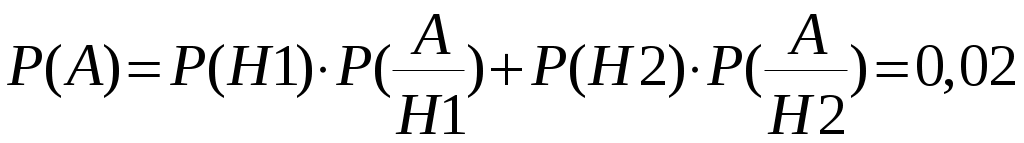

    Ответ: 0,02.

    Задание 3. Случайные величины
    Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины, заданной рядом распределения


    ξ
    -2
    0
    2
    5

    р
    0.1
    0.5
    0.3
    0.1



    Решение.
    Запишем формулу для вычисления математического ожидания и подставим в неё данные задачи:

    Запишем формулу для вычисления дисперсии и подставим в неё данные задачи:


    Среднее квадратическое отклонение вычисляется по формуле:

    Ответ:

    Задание 4. Нормальное распределение случайной величины.
    Случайная величина распределена по нормальному закону с параметрами a, σ. Найдите вероятность того, что случайная величина принимает значения из интервала [k1; k2].
    параметр a
    параметр σ
    значение k1
    значение k2

    Вариант 2
    7
    2
    5
    10



    Решение.
    Вероятность попадания нормально распределённой величины в интервал вычисляется по формуле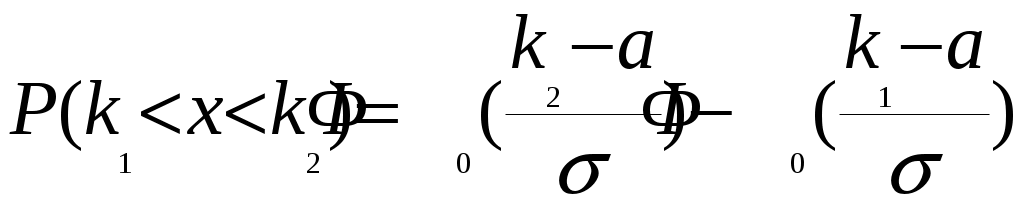

    где Фo(x) - функция Лапласа, её значения можно найти в таблице в конце любого учебника по теории вероятностей.
    Согласно условиям задачи, имеем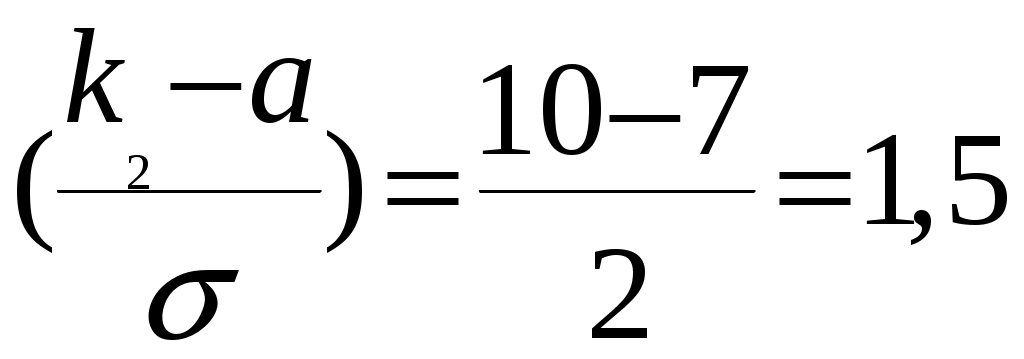



    в таблице находим значение Фo(1,5) = 0,4331928;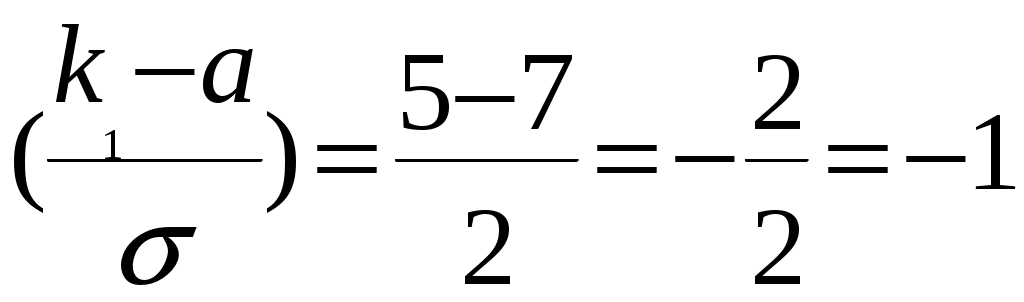

    в таблице находим ближайшее значение Фo (1) = 0,3413447; с учётом того, что функция Лапласа нечётная, получаем Фo (-1) = −0,3413447;
    подставим в формулу:

    Ответ: 0,7745375.
    Список используемой литературы


    1. Агульник, В. И.Теориявероятностей и математическая статистика [Электронный ресурс] : учеб. прогр. и контр. задания / В. И. Агульник, О. Н. Агульник ; Сиб. гос. ун-т телекоммуникаций и информатики. - Электрон. дан. (1 файл). - Новосибирск : СибГУТИ, 2012. - 19 с. - Библиогр.: с. 3. - Загл. с титул. экрана. - Электрон. версия печ. публикации. - Режим доступа: http://ellib.sibsutis.ru/ellib/2012/393_AgulnikUchProgrKontrZadTV.pdf по паролю – Полнотекстовая база данных учебных и методических пособий СибГУТИ.



    2. Рябко, Б. Я. Сборник задач по теории вероятностей и основам теории массового обслуживания [Электронный ресурс] : учеб. пособие / Б. Я. Рябко ; Сиб. гос. ун-т телекоммуникаций и информатики. - Переизд. - Электрон. дан. (1 файл). - Новосибирск : СибГУТИ, 2010. - 76 с. : ил. - Загл. с титул. экрана. - Электрон. версия печ. публикации. - Режим доступа: http://ellib.sibsutis.ru/ellib/2010/317_Ryabko_Teor_ver.rar по паролю – Полнотекстовая база данных учебных и методических пособий СибГУТИ.

    3. Балдин К.В. Теория вероятностей и математическая статистика [Электронный ресурс] : учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. — Электрон. текстовые данные. — М. : Дашков и К, 2014. — 473 c. — 978-5-394-02108-4. — Режим доступа: http://www.iprbookshop.ru/4444.html .— ЭБС «IPRbooks»

    написать администратору сайта