Задачи по теорверу. Контрольная работа по дисциплине Теория вероятности и математическая статистика

• Название: Контрольная работа по дисциплине Теория вероятности и математическая статистика
• Анкор: Задачи по теорверу
• Дата: 06.12.2021
• Размер: 103.97 Kb.
• Имя файла: kr.docx
• Тип: Контрольная работа; #293280

Контрольная работа

по дисциплине «Теория вероятности и математическая статистика»



Ответы:

1. 0.555

2. 0,0512

3. (1.81;7.24)

4.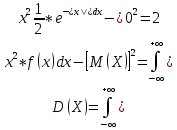

Задача 1.

В качестве оценки наибольшего правдоподобия неизвестной вероятности р биномиального распределения: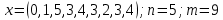





Ответ: 0.555

Задача 2.

Вероятность выбрать отличника в одной группе равна p=1/5.

Выбор отличника будем считать успехом.

Тогда число успехов среди n=5 испытаний должно равняться m=3.

Таким образом, по основной формуле схемы Бернулли искомая вероятность равна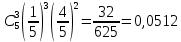


Ответ: 0,0512

Задача 3.

Таблица для расчета показателей.

№	xi	(x-xср)2
1	1232.4	6.923
2	1232.6	5.911
3	1232.8	4.978
4	1233.7	1.772
5	1233.8	1.516
6	1234	1.063
7	1234.7	0.11
8	1234.9	0.0172
9	1235.1	0.00473
10	1235.4	0.136
11	1235.7	0.447
12	1236.3	1.61
13	2474	7.752
14	1237.1	4.28
15	1238	8.813
∑	19760.5	45.334

Выборочная средняя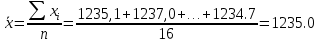



Исправленная дисперсия S



Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна P(χ²_n-1 < h_H) = γ/2 = 0.04. Для количества степеней свободы k=n-1=15, по таблице распределения χ² находим:
χ²(15;0.04) = 24.99579.
Случайная ошибка дисперсии нижней границы:



Вероятность выхода за верхнюю границу равна P(χ²_n-1 ≥ h_B) = 1 - P(χ²_n-1 < h_H) = 1 - 0.04 = 0.96:
χ²(15;0.96) = 6.26214.
Случайная ошибка дисперсии верхней границы: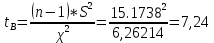



Таким образом, интервал (1.81;7.24) покрывает параметр S² с доверительной вероятностью 0.92

Задача 4.

Из условия нормировки функции плотности распределения находим параметр :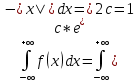



Получаем параметр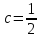



Функция плотности распределения: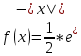



Математическое ожидание: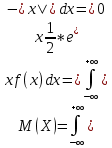



Дисперсия: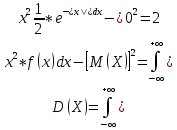