ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА по дисциплинеМДК МДК 04.03 Статистическая обработка информации. ДКР МДК 04.03. Контрольная работа по дисциплинемдк мдк 04. 03 Статистическая обработка информации Студент (Ф. И. О. полностью)
 Скачать 46.6 Kb. Скачать 46.6 Kb.
|
|
Санкт Петербургское государственное бюджетное профессиональное образовательное учреждение «Академия управления городской средой, градостроительства и печати» ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА по дисциплине/МДК МДК 04.03 Статистическая обработка информации Выполнил: Студент (Ф.И.О. полностью) Специальность 38.02.01 Экономика и бухгалтерский учёт (по отраслям) (Код и наименование специальности) ПРОВЕРИЛ: Преподаватель_________/____________/ ПодписьФИО Оценка _________ «_____________________» «___»_________20___г. Вариант №5 Задание 1: Ответить письменно на вопросы: Выборочные наблюдения(генеральная совокупность, способы формирования выборочной совокупности, понятие объёма выборки). Исследования связей между явлениями (понятия, задачи, корреляционный анализ, методы регрессивного анализа). Ответ: Выборочное наблюдение–несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность. Выборочное наблюдение нельзя отождествлять с несплошным обследованием вообще, т.к. оно является лишь одним из видов последнего, наиболее проработанным с методологической и организационной точек зрения. Помимо выборочного наблюдения несплошное обследование может осуществляться путем монографического описания, метод основного массива. При выборочном методе обследованию подвергается сравнительно небольшая часть всей изучаемой совокупности (обычно до 5-10%, реже 15-25%). Преимущества выборочного метода: 1) существенная экономии различного вида ресурсов: финансовых средств, материально-технических ресурсов, трудовых ресурсов, времени. 2) возможность расширить программу наблюдения, т.е. более детально изучить отдельные единицы совокупности; 3) невозможность в ряде случаев проведения сплошного наблюдения (например, контроль качества многих видов продукции связан с их порчей). Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей. Генеральная совокупность – исходная изучаемая статистическая совокупность, из которой производится отбор части единиц. Выборочная совокупность (выборка) – отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию Практика применения выборочного метода в экономико-статистических исследованиях использует следующие способы отбора единиц из генеральной совокупности: 1) индивидуальный отбор — в выборку отбираются отдельные единицы; 2) групповой отбор — в выборку попадают качественно однородные труппы или серии изучаемых единиц; 3) комбинированный отбор - комбинация индивидуального и группового отбора. Способы отбора определяются правилами формирования выборочной совокупности. Выборка может быть: 1) собственно-случайная; 2) механическая (систематическая); 3) типическая (стратифицированная, расслоенная); 4) серийная (гнездовая); Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. Единицы отбираются в случайном порядке, не зависящем ни от последовательности расположения единиц в совокупности, ни от значений их признаков. Все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку. При этом следует установить четкие границы генеральной совокупности. Отбор производится с использованием какого-либо алгоритма, реализующего принцип случайности, например, методом жеребьевки. Объем жребиев (фишек, карточек) должен соответствовать объему генеральной совокупности. Каждый жребий должен содержать информацию об отдельной единице совокупности – номер, название, ФИО, адрес или какой-либо другой отличительный признак. Требуемое в соответствии с установленным процентом отбора число жребиев извлекается из общей совокупности в случайном порядке. Можно использовать и таблицы случайных чисел. Для этого берется любая строка или колонка таблицы, и в выборку включаются указанные номера единиц генеральной совокупности. Собственно-случайная выборка может быть осуществлена по схемам повторного и бесповторного отбора. Механическая (систематическая) выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей. Так, если из совокупности 500 000 ед. предполагается отобрать 10 000 ед., то пропорция отбора составит 1 /50, т.е. отбирается каждая 50-я единица. Интервал отбора также может быть определен по установленному проценту отбора. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой такой группы в выборку отбирается лишь одна единица. Для обеспечения репрезентативности (представительности) выборки все единицы генеральной совокупности должны располагаться в определенном порядке. При этом по отношению к изучаемому показателю единицы генеральной совокупности могут быть упорядочены по существенному, второстепенному или нейтральному признаку. Это важно для установления порядка отбора единиц в выборку. При упорядочении генеральной совокупности по существенному признаку, т.е. по признаку, который всецело определяет поведение изучаемого показателя, в выборочную совокупность должна отбираться та единица, которая находится в середине каждой группы. Это позволяет избежать появления систематической ошибки выборки. Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осуществить, не прибегая к составлению списков. На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или поточной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т. д. Типическая (стратифицированная, расслоенная) выборка используется в тех случаях, когда все единицыгенеральной совокупности объединены в несколько крупных типических групп. Такие группы называются также стратами, или слоями. Например, при обследовании населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные и образовательные группы, при обследовании предприятий – отрасли, формы собственности и т.п. Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой вариации (дифференциации) признака. При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом: где N – численность генеральной совокупности; Ni–объем i-ой группы генеральной совокупности; n – численность выброки; ni - объем выборки из i-ой группы: Логика отбора пропорционально вариации заключается в следующем: если внутри какой-либо типической группы наблюдаемый признак варьирует слабо, то для определения границ генеральных характеристик из данной группы достаточно обследовать относительно небольшое число единиц; при сильной же вариации признака объем выборки из данной группы должен быть соответственно увеличен. Серийная (гнездовая) выборка используется в тех случаях, когда все единицыгенеральной совокупности объединены в небольшие более или менее равновеликие группы (серии). В качестве таких серий могут выступать упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и т.п. При серийной выборке отбираются не отдельные единицы, а целые их группы, серии (гнезда). Группы единиц (серии) отбираются собственно-случайным или механическим способом. Внутри же каждой из попавшей выборку серии обследуются все без исключения единицы, т.е. применяется сплошное наблюдение. В отдельных случаях серийная выборка имеет не столько методологические, сколько организационные преимущества перед другими способами формирования выборочной совокупности. Например, многие товары хранятся в пачках, коробках, ящиках и т.п. Поэтому при контроле качества поступившего в упаковке товара рациональнее проверить несколько отдельных упаковок, чем из всех упаковок отобрать необходимое количество единиц товара. Задание 2: Рассчитать средний возраст студентов в группе из 20 человек:
Решение: Если сгруппировать данные, то получится ряд распределенийя
= 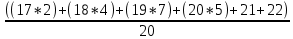 = 19,1 = 19,1 Ответ:_19,1'>Ответ: 19,1 средний возраст студентов Задание 3: Распределение рабочих по выработке деталей:
Определите среднюю выработку деталей рабочими за смену. Решение: Рабочих всего: 7+16+10+6+6=45 Средняя арифметическая взвешенная = (18*7) +(19*16)+(20*10)+(21*6)+(22*6)=126+304+200+126+132= 888/45= 19,73 ≈ 20 Ответ: ≈ 20 деталей средняя выроботка рабочим за смену. Задание 4: Распределение рабочих АО по уровню ежемесячной оплаты труда
Определить среднюю оплату труда на одного рабочего Решение: (450*10)+(550*20)+(650*25)+(750*35)+(850*21)+(950*19)= 45000+11000+16250+26250+17850+18050=134400 10+20+25+35+21+19=130 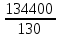 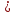 1033,84 1033,84Ответ: средняя оплата труда на одного рабочего 1033,84 у.е. Задание 5: Найти моду и медиану.
Решение : В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1059) Вычисление величины моды: 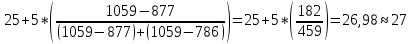 Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части. Для начала необходимо узнать сумму накопленных частот интервалов, предшествующих медианному: 351+877=1228 Сумма частот : 351+877+1059+786+218+126+82=3499 Вычисление медианы по формуле: 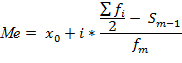 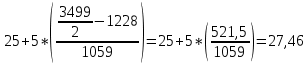 Ответ: модальный возраст студентов равен 27 годам, половина студентов имеет возраст до 27,46 года, а другая свыше 27,46 года. Задание 6: Определите среднегодовую стоимость имущества: 1) за I квартал, 2) за II квартал, 3) за полугодие в целом:
Решение: Средняя стоимость имущества за I квартал: 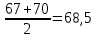 Средняя стоимость имущества за II квартал: 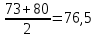 Средняя стоимость имущества за полугодие в целом: 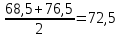 Ответ: среднегодовая стоимость имущества за I квартал – 68,5, за II квартал – 76,5, за полугодие в целом – 72,5 Задание 7: Кредиторская задолженность предприятий района за отчетный период характеризуется данными тыс. руб:40, 60, 80, 50, 74, 90, 120, 45, 70, 92,100, 52, 67, 83, 70, 74, 63, 75, 85, 110. Постройте ряд распределения предприятий по размеру кредиторской задолженности, образовав 4 группы с равными интервалами и изобразите его графически Решение:
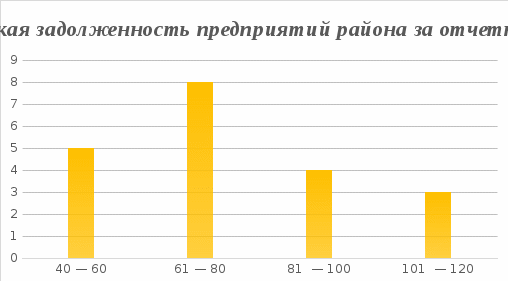 Задание 8: Объём экспорта продукции предприятия составляет:
Определить средний уровень моментного ряда. Решение: 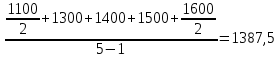 Ответ: средний уровень моментного ряда – 1387,5. |
