Контрольная работа по Электромагнитным полям и волнам. Руководитель Федосеева Е. В. (фамилия, инициалы)
 Скачать 311 Kb.
|
 Министерство образования и науки Российской ФедерацииФедеральное агентство по образованию Муромский институт (филиал) федерального бюджетного государственного образовательного учреждения высшего профессионального образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых» Факультет ФРЭКС Кафедра Радиотехника КОНТРОЛЬНАЯ РАБОТА по Электромагнитным полям и волнам. Руководитель Федосеева Е.В . (фамилия, инициалы) (подпись) (дата) Студент РТз-116 . (группа) Агафонов П.С. (фамилия, инициалы) (подпись) (дата) Муром 2017  СодержаниеЗадание 1: Плоские электромагнитные волны в неограниченной среде…...…3 Задание 2: Падение электромагнитной волны на плоскую границу раздела двух диэлектрических сред…………………………………………………....9 Список литературы……………………………………………………………13 Задание 1: Плоские электромагнитные волны в неограниченной среде.  В материальной среде с параметрами  ,  ,  в выбранной системе координат вдоль оси  распространяется плоская электромагнитная волна, комплексная амплитуда напряженности электрического поля которой в точке с координатой  определяется выражением . Частота волны  . Необходимо определить:- поляризационные характеристики волны; - фазовую скорость; - длину волны; - коэффициент ослабления волны в среде; - комплексную амплитуду вектора плотности полного тока в точке с координатой  и  .- волновое сопротивление среды; - комплексную амплитуду напряженности магнитного поля волны; - комплексный вектор Пойнтинга и его среднее значение. Решение. Для оценки поляризационной структуры волны проанализируем соотношение амплитуд и фаз составляющих вектора электрического поля.  ,  ,  .Так как составляющие 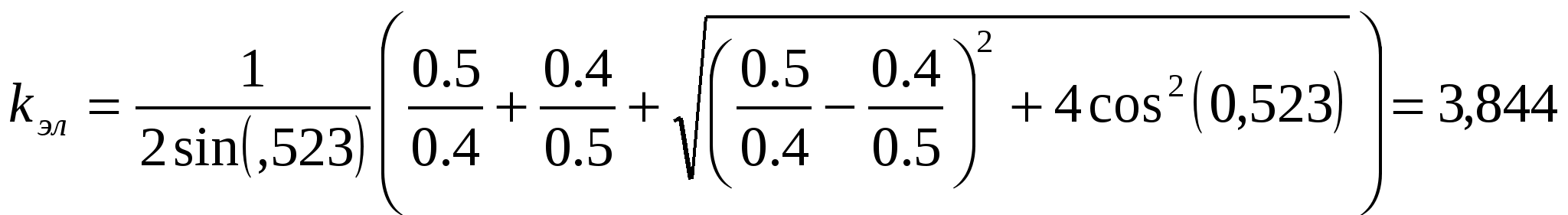 и  не равны между собой и  , волна имеет эллиптическую поляризацию. Определим параметры поляризации волны:  - коэффициент эллиптичности  (2.13) ,- угол наклона 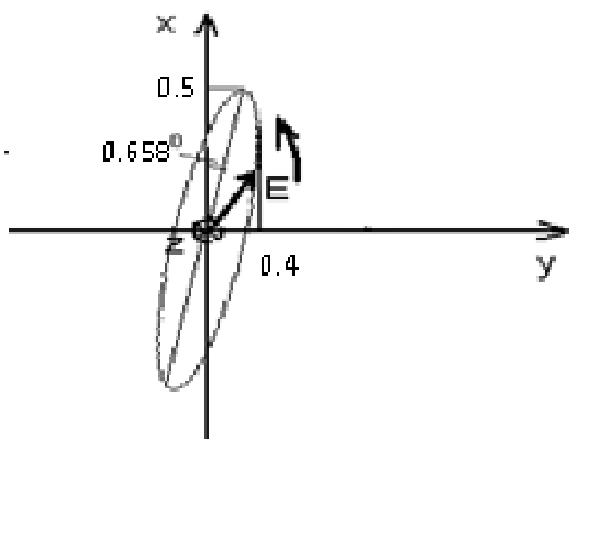 большой оси эллипса к оси x (2.14) .Так как отстает по фазе от на  , то заданная волна имеет левокруговую эллиптическую поляризацию с параметрами  и  (рис. 2.4) Рис. 2.4 Поляризационная структура волны. Волна распространяется в среде с проводимостью, следовательно, необходимо учитывать потери, поэтому фазовую скорость определяем по (2.18) с учетом (2.16) 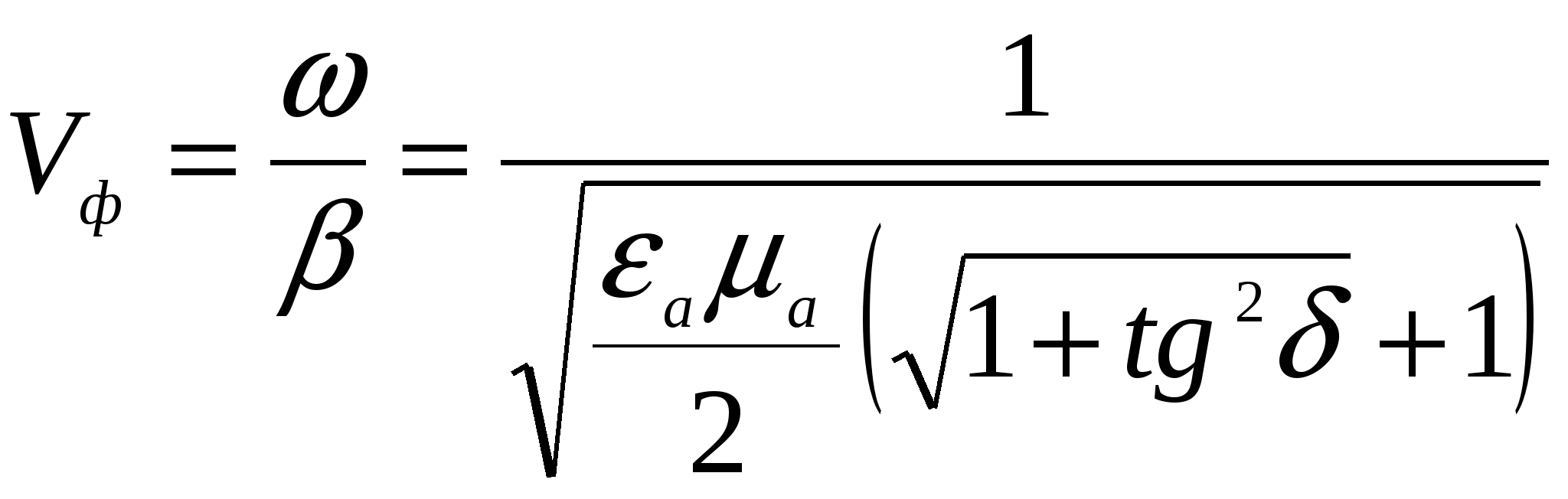 ,где тангенс угла потерь равен  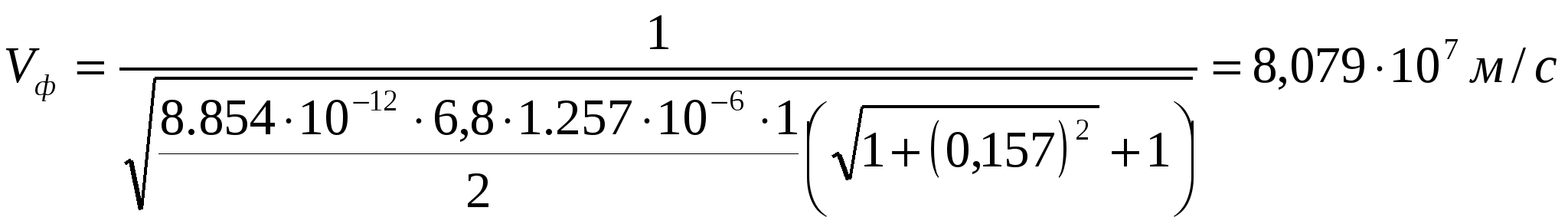 . .Длина волны в среде с потерями отличается от ее величины в свободном пространстве 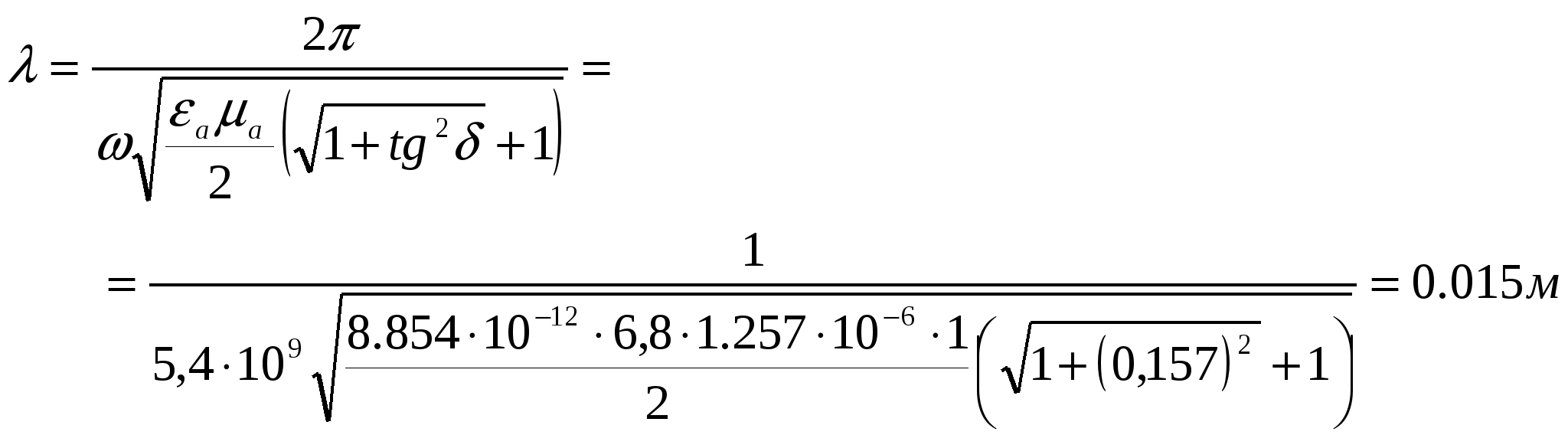 . В рассматриваемом случае  . Длина волны в заданной среде определяется по (2.19) и равна Коэффициент ослабления волны в среде рассчитывается по (2.17) и равен 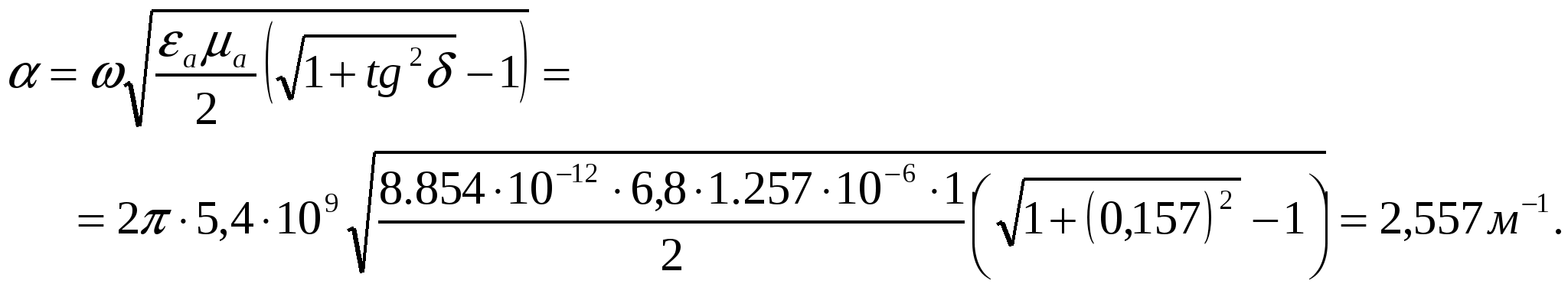 Полученный результат говорит о сильном затухании волны в среде, т.е. при прохождении волной расстояния в 1м ее амплитуда уменьшается в 2,557 раз. Полный ток, возникающий в среде при распространении заданной волны, определяется суммой токов проводимости и тока смещения. Плотность полного тока  из условий (2.5) и (2.6) равна . Амплитуда вектора плотности полного тока с учетом потерь в заданной среде равна  . Фаза плотности полного тока определяется соотношением  , где  - фаза составляющих вектора напряженности электрического поля.Для точки среды с координатой  амплитуда вектора плотности полного тока равна а для точки с координатой   Фазы составляющих вектора плотности полного тока равны 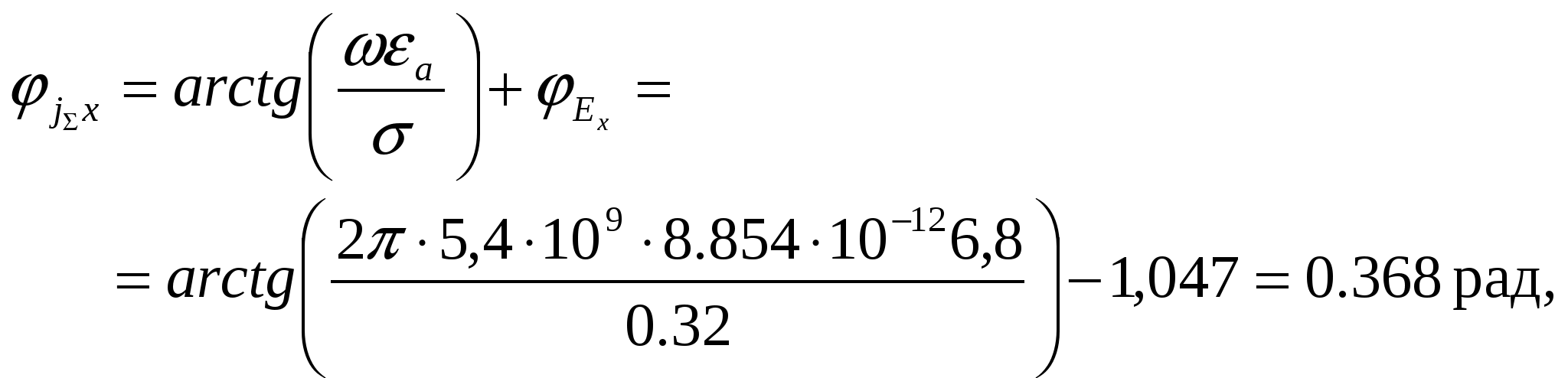  .В результате вектор плотности полного тока может быть представлен следующим образом: - в точке среды с координатой   , - в точке среды с координатой  .Волновое сопротивление среды с потерями определяется по (2.20) с учетом, что 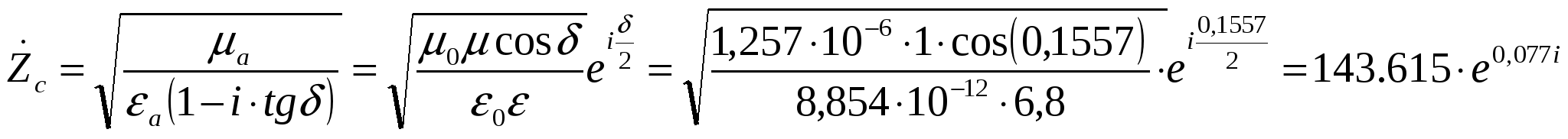 ,   Комплексная амплитуда напряженности магнитного поля задается выражением (2.15) 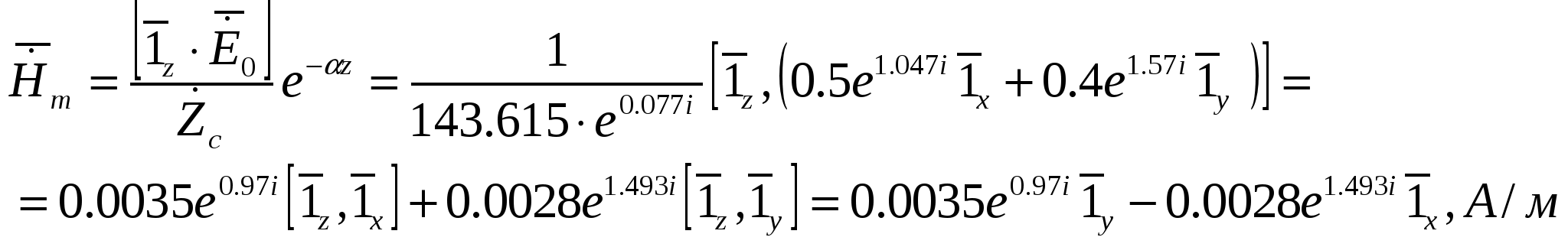 Комплексный вектор Пойнтинга определяется по (2.7) и с учетом, что 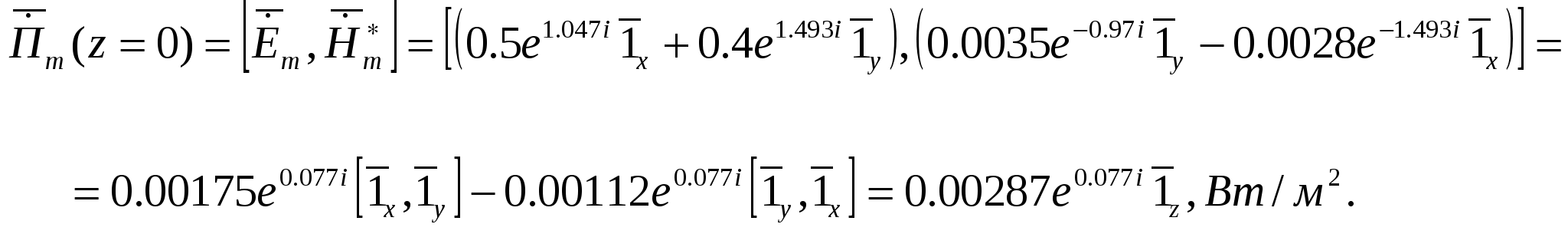 и  , в точке с координатой он равен   Среднее значение вектора Пойнтинга рассчитывается по (2.8) Значения вектора Пойтинга в точке среды с координатой определяются по выражениям  и  и равны   . Задание 2:Падение электромагнитной волны на плоскую границу раздела двух диэлектрических сред. Плоская электромагнитная волна с напряженностью электрического поля  и частотой  падает под углом  из среды с параметрами  на границу со средой с параметрами  . Причем плоскость XOZ – плоскость падения, а плоскость YOZ – плоскость раздела двух сред. Определить:- коэффициенты отражения и преломления волны от границы раздела сред; - комплексные амплитуды отраженной и преломленной волн. Решение Из законов Снеллиуса (3.1), (3.2) определим углы отражения и преломления для данной волны. Угол отражения равен  , угол преломления  .Для определения коэффициентов отражения и преломления по формулам (3.3) и (3.4) найдем волновые сопротивления граничащих сред  , .Заданная волна содержит две составляющие  и  , следовательно, необходимо рассмотреть по отдельности их прохождение через границу сред, т.к. при указанной ориентации системы координат  составляющая соответствует случаю нормальной поляризации, а - параллельной поляризациюНайдем значения коэффициентов отражения и преломления для двух поляризаций по формулам (3.3) - (3.4) и (3.9) - (3.10) соответственно. Для нормальной поляризации - коэффициент отражения  ,- коэффициент преломления  .Для параллельной поляризации - коэффициент отражения  ,- коэффициент преломления  .Найдем выражения для напряженности электрического поля отраженной и преломленной волн.  ,  ,  Определим критический угол падения волны на границу раздела заданных сред.  . (12)-этого явления не существует, следовательно падающая волна полностью отражается от границ сред.Если волна падает на границу раздела сред под углом  , то коэффициенты отражения равны  ,  . Напряженность электрического поля отраженной волны равна Найдем значения углов Брюстера для двух видов поляризации. Для параллельной поляризации  , соответственно  .Для нормальной поляризации 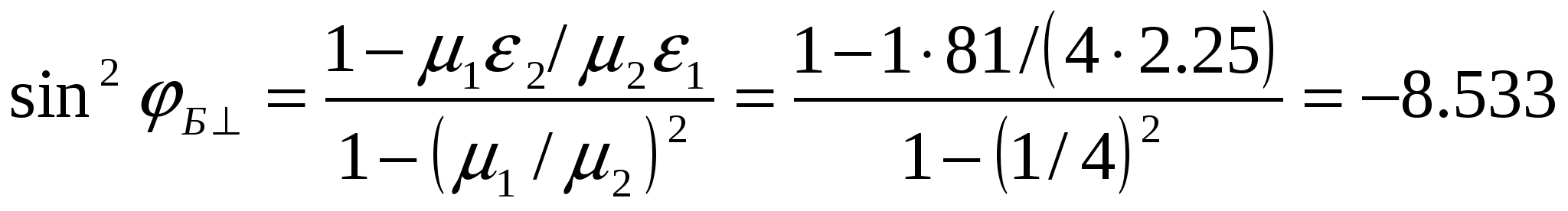 Таким образом, только при параллельной поляризации при угле падения  наблюдается полное прохождение волны во вторую среду. При этом угол преломления будет равен  Найдем значения коэффициентов отражения и преломления для угла падения . , , , .Напряженность электрического поля отраженной и преломленной волны для угла падения равна , .Список литературы Электромагнитные поля и волны: метод. указания к контрольной работе/ сост. Е.В.Федосеева. – Муром: Изд.-полиграфический центр МИ ВлГУ, 2011. – 60 с.– Библиогр. 5 назв.  |