Электротехника_Задачи. Контрольная работа по курсу "Электротехника" Обучающегося Ф. И. О группы Проверил

• Название: Контрольная работа по курсу "Электротехника" Обучающегося Ф. И. О группы Проверил
• Дата: 11.04.2022
• Размер: 128.77 Kb.
• Имя файла: Электротехника_Задачи.docx
• Тип: Контрольная работа; #461861

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ Российской Федерации

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ университет»
Кафедра электроэнергетики
Контрольная работа

по курсу

"Электротехника"

Обучающегося Ф.И.О

группы ____________


Проверил

_________________/ Е.П. Власова


Тюмень 2021 г.
Контрольное задание 1 .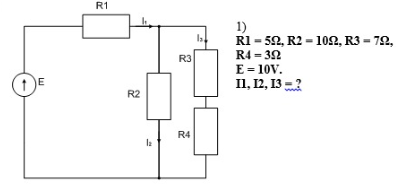


Требуется найти токи в ветвях, используя законы Кирхгофа.
Решение:

1. Произвольно выбираем и указываем на схеме направления токов в ветвях. Обозначаем узлы схемы. Показываем направления обхода контуров.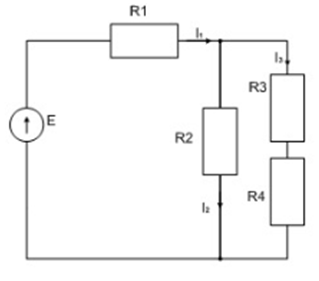


2. В схеме имеем три неизвестных тока (I₁ – I₃), следовательно, система должна состоять из трех уравнений (К_ур=3).

3. В схеме два узла (К_узлов = 2), следовательно по первому закону Кирхгофа необходимо составить одно узловое уравнения (К_ур1зак= К_узлов–1=2–1=1) – на одно уравнение меньше, чем количество узлов.

4. Остальные (контурные) уравнения составляются по второму закону Кирхгофа ((Кур2зак = = К_ур – К_ур1зак = 3 – 1 = 2).

5. Согласно первому закону Кирхгофа, алгебраическая сумма токов в узле электрической цепи равна нулю. Знак тока выбираем в зависимости от направления тока – к узлу или от узла.

6. Согласно второму закону Кирхгофа, алгебраическая сумма падений напряжений на сопротивлениях контура равна алгебраической сумме ЭДС этого контура. Знак падения напряжения (тока) и ЭДС определяется в зависимости от его направления по отношению к направлению обхода контура.

7. В соответствии с пунктами 2-6 получаем следующую систему уравнений: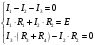



8. Подставляем численные значения и решая систему, находим токи в ветвях: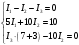





Ответ: А, А, А.

Контрольное задание 2 .
Дано: Uл= 220 В, r₁= 30 Ом, r₂= 17 Ом, r₃=15 Ом, X_L= 25 Ом, Хс=14 Ом.


Определить фазные и линейные токи для заданной схемы, а также ток в нейтральном проводе.
Решение:

При соединении фаз "звездой" линейные токи равны фазным.

Считаем, что вектор фазного напряжения U_a направлен по действительной оси

1. 
   Напряжения фаз
   

2. 
   Сопротивление фаз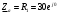
   

 

3. 
   Токи в фазах
   

А

А

А.
4) Ток в нейтральном проводе

  А.

Контрольное задание 3 .

Номинальная мощность трехфазного асинхронного двига­теля с короткозамкнутым ротором Р_н = 10 кВт,

номинальное напряже­ние U_н = 380В,

номинальное число оборотов ротора n_н = 1420 об/мин,

номинальный к.п.д. 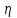 = 0,84 и

номинальный коэффициент мощности Cos φ = 0,85.

Кратность пускового тока I_п / I_н = 6,5,

перегру­зочная способность двигателя l = 1,3.

Определить: 1) потребляемую мощность; 2) номинальный и макси­мальный (критический) вращающие моменты; 3) пусковой ток; 4) номи­нальное скольжение; 5) построить механические характе­ристики М= f(s) и n = f(М).

 

Решение:

1. 
   Потребляемая мощность
   

кВт

 

2. 
   Номинальный и максимальный моменты:
   

Нм

Нм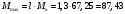

 

3. 
   Номинальный и пусковой ток:
   

  А

 А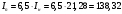

 

4. 
   Номинальное и критическое скольжение:
   

 

.

 

5. 
   Механические характеристики М = f(s) и n = f(М) строятся по уравнению:
   

Задаваясь скольжением s от 0 до 1, подсчитываем вращающий момент. Скорость вращения ротора определяем из уравнения:

n = n₀ (1 - S)

Расчётные данные приведены в таблице 1. Характеристики, построенные по данным таблицы 1, изображены на рис. 1 и рис. 2.

Таблица 1

S	M	n
0,053	67,25	1420
0,1	86,72	1350
0,114	87,43	1329,5
0,2	75,11	1200
0,3	57,92	1050
0,4	45,97	900
0,5	37,79	750
0,6	31,97	600
0,7	27,66	450
0,8	24,35	300
0,9	21,73	150
1	19,62	0

Рис. 1 - Механическая характе­ристика М= f(s)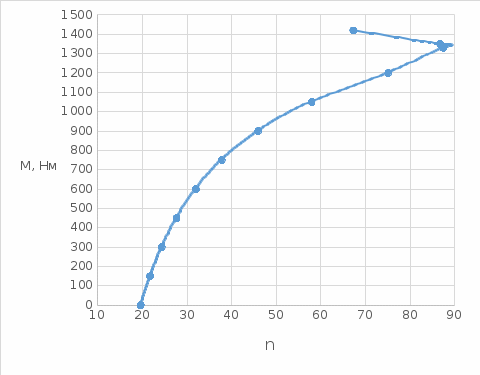


Рис. 2 - Механическая характе­ристика n= f(M)