КР по МС решение варианта. Контрольная работа по математической статистике

• Название: Контрольная работа по математической статистике
• Дата: 19.09.2021
• Размер: 401.5 Kb.
• Имя файла: КР по МС решение варианта.doc
• Тип: Контрольная работа; #234196

Контрольная работа по математической статистике
Вариант №А

1. 
   В команду должны быть отобраны 4 спортсмена из имеющихся 10. Сколькими способами это можно сделать, если два определенных спортсмена должны войти в команду?
   

Решение. Поскольку два спортсмена уже отобраны в команду, то остается отобрать 2 спортсмена из 8 оставшихся. Так как порядок отбора спортсменов в команду неважен, то сформировать команду можно

способами.

2. 
   В урне находится 12 шаров. Все они пронумерованы от 1 до 12. Опишите событие , если A={шар с номером кратным 3}, B={шар с номером меньше 5}.
   

Решение. Опишем события A={3, 6, 9, 12} и B={1, 2, 3, 4}. Тогда и .

3. 
   Электрическая схема имеет вид: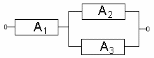
   

Используя алгебру событий, опишите событие, описывающие безотказную работу цепи.

Решение. Цепь будет работать, если будет работать элемент A₁ и хотя бы один элемент A₂ и A₃, т.е. событие, описывающее безотказную работу цепи имеет вид

.

4. 
   На каждой из шести одинаковых карточках напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вытянутых по одной и расположенных «в одну линию» карточках, можно будет прочесть слово «трос».
   

Решение. Расположить четыре карточки можно способами. Число благоприятствующих случаев равно , т.е. слово «трос» можно составить только одним способом. Таким образом, искомая вероятность будет равна

.

4. 
   Брошены две игральные кости. Найти вероятность того, что выпадет хотя бы одно четное число.
   

Решение. При бросании двух костей может выпасть случаев. Число случаев, когда выпадут только нечетные числа, будет равно . Следовательно, число случаев, когда выпадет хотя бы одно четное число, будет равно . Таким образом, искомая вероятность будет равна

.

4. 
   Для проверки собранной схемы последовательно послано три одиночных импульса. Вероятности прохождения каждого из них не зависят от того, прошли остальные или нет, и соответственно равны 0,9, 0,8 и 0,7. Определить вероятность того, что пройдут ровно два посланных импульса.
   

Решение. Пусть A={прошел первый импульс}, B={прошел второй импульс}, C={прошел третий импульс}. Опишем событие, что пройдут только два импульса

.

Поскольку события A, B, C – независимые, а каждое слагаемое – несовместные события, то

.

Учитывая, что P(A)=0,9, , P(B)=0,8, , P(C)=0,7, , получим

.

4. 
   Всхожесть некоторых семян составляет 30%. Найти вероятность того, что из 6 посаженных семян взойдет больше половины.
   

Решение. Здесь нужно найти вероятность

.

Воспользуемся формулой Бернулли



По условию задачи n=6, p=0,3, q=0,7. Тогда

,

,

,

Таким образом,

4. 
   Число автобусов, прибывающих каждые 10 мин на определенную остановку, случайная величина X, заданная так:
   

X	0	1	2	3	4	5	6	7
P	0,05	0,05	0,15	0,2	0,25	0,15	0,1	0,05

а) Определить ожидаемое число прибываемых автобусов, а также дисперсию и среднее квадратическое отклонение.

б) Определить, чему равна вероятность того, что в какой-то промежуток времени число прибывающих автобусов превысит ожидаемое.

Решение. а) Определим ожидаемое число прибываемых автобусов, т.е. математическое ожидание



При вычислении дисперсии предварительно найдем



Тогда



и

.

б) В данном случае требуется найти вероятность

.

4. 
   Дискретная случайная величина X имеет только два возможных значения: x₁ и x₂, причем x₁<x₂. Найти закон распределения X, зная математическое ожидание M[X]=1,4, дисперсию D[X]=0,24 и вероятность P(X=x₁)=p₁=0,6.
   

Решение. Сумма вероятностей всех возможных значений X равна единице, поэтому вероятность того p₂, что X примет значение x₂, равна 1–0,6=0,4. Запишем закон распределения дискретной случайной величины X:

X	x1	x2
P	0,6	0,4

Для отыскания x₁ и x₂ составим два уравнения. По определению

M[X] = = x₁p₁+x₂p₂+ ... +x_np_n.

Учитывая, что по условию М[X] = 1,4, запишем первое из уравнений:

.

Принимая во внимание, что по условию D[X] = 0,24, и используя равенство

,

напишем второе уравнение:

, или .

В результате получается следующая система уравнений:



Выразив x₁ из первого уравнения и подставив его во второе, получим квадратное уравнение

.

Отсюда находим два решения: и (отсюда получаем также, что и ). По условию , поэтому задаче удовлетворяет только первое решение. Таким образом, искомый закон распределения имеет вид

X	1	2
P	0,6	0,4

4. 
   Фирма, торгующая продуктами питания для животных, желает оценить объём ежедневной продажи упаковок питания определённого сорта. Считая, что объём продаж описывается нормальным законом распределения с параметрами a=80,2 и =5,1: а) найти вероятность того, что объём продаж будет больше 90. б) Было объявлено, что объём продаж равен 100. Можно ли доверять такой информации?
   

Решение. а) Для нормального распределения вероятность того, что случайная величина примет значения в заданном интервале, находится по формуле

.

Пользуясь этой формулой

,

т.е. вероятность того, что объём продаж будет больше 90, очень мала.

б) Найдём «трехсигмовый интервал»:

.

Поскольку значение X=100 не попадает в этот интервал, то в соответствие с правилом «трех сигм» такое значение случайной величины маловероятно, практически невозможно. Поэтому информации о том, что объем продаж составил 100 нельзя доверять.

4. 
   Получены сгруппированные данные о дневной выручке в компьютерном салоне-магазине (тыс. руб.):
   

Сумма продаж	0-100	100-200	200-300	300-400	400-500	500-600
Число продаж	4	8	11	21	15	14

а) Найти среднее арифметическое, дисперсию и среднее квадратическое отклонение.

б) Постройте гистограмму

Решение. а) Составим расчетную таблицу

Сумма продаж	Число продаж, n	Середина интервала, x	nx	nx2	n/h
0-100	4	50	200	10000	0,04
100-200	8	150	1200	180000	0,08
200-300	11	250	2750	687500	0,11
300-400	21	350	7350	2572500	0,21
400-500	15	450	6750	3037500	0,15
500-600	14	550	7700	4235000	0,14
Сумма	73	–	25950	10722500

В соответствии с данными таблицы находим среднее арифметическое

.

Далее находим

,

,

.

б) Построим гистограмму. Для этого над каждым интервалом строим прямоугольник высотой, равной n_i/h, где h – длина интервала, т.е. площадь каждого прямоугольника равна частоте.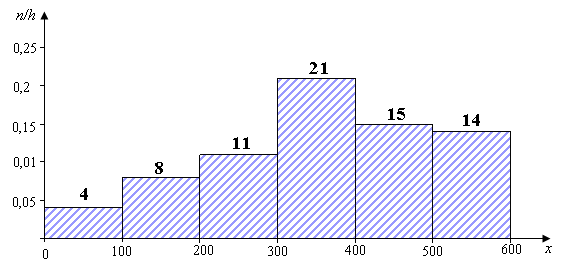

4. 
   Некоторая компания провела рекламную кампанию в магазинах с демонстрацией антисептических качеств своего нового моющего средства. Через 10 недель компания решила проанализировать эффективность этого вида рекламы, сопоставив еженедельные объемы продаж (y) с расходами на рекламу (x).
   

Расходы на рекламу, тыс. руб	5	8	6	5	3	9	12	4	3	10
Объем продаж, тыс. руб.	72	76	78	70	68	80	82	65	62	90

а) Рассчитайте коэффициент корреляции. Сделайте вывод.

б) Рассчитайте коэффициенты линейной регрессии дайте интерпретацию полученных результатов.

в) Постройте корреляционное поле, а также уравнение регрессии.

Решение. а) Составим расчетную таблицу

№	Расходы на рекламу, тыс. руб, x	Объем продаж, тыс. руб., y	x2	y2	xy
1	5	72	25	5184	360
2	8	76	64	5776	608
3	6	78	36	6084	468
4	5	70	25	4900	350
5	3	68	9	4624	204
6	9	80	81	6400	720
7	12	82	144	6724	984
8	4	65	16	4225	260
9	3	62	9	3844	186
10	10	90	100	8100	900
Сумма	65	743	509	55861	5040

В соответствии с данными таблицы находим:

, , , ,

, , , ,

.

Далее находим коэффициент корреляции

.

Таким образом, между расходами на рекламу и объемом продаж существует сильная корреляционная зависимость, т.е. чем больше расходы на рекламу тем больше будут объемы продаж.

б) Найдем уравнение линейной регрессии

,

где

, .

Таким образом, уравнение регрессии будет иметь вид



Коэффициент b означает, что при увеличении расходов на рекламу на 1 тыс. руб. объемы продаж в среднем увеличатся на 2,43 тыс. руб.

в) Построим корреляционное поле. Для этого на рисунке точками отметим исходные данные. На их фоне изобразим прямую регрессии, в соответствии в полученным уравнением регрессии.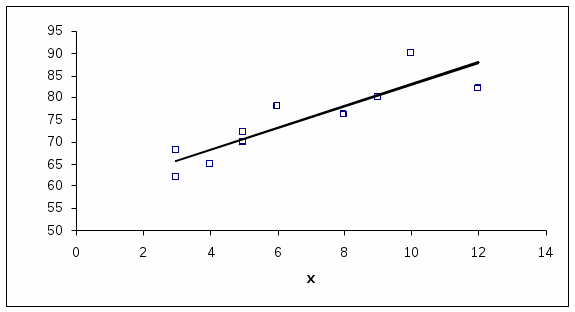