Контрольная работа по МА зо Экономика. Контрольная работа по Математическому анализу для студентов 1 курса зо экономического факультета
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Контрольная работа по Математическому анализу для студентов 1 курса з/о экономического факультета направление «Экономика» Задание 1 Найдите область определения функции 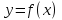 . .
Задание 2 Найдите функцию обратную функции 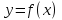 . Укажите область определения прямой и обратной функций. . Укажите область определения прямой и обратной функций.
Задание 3 Найдите пределы следующих функций, не используя правило Лопиталя: Серия А 1 1) 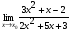 при а) при а) 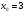 ; б) ; б) 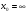 ; в) ; в) 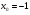 ; ;2) 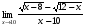 ; 3) ; 3) 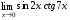 ; 4) ; 4) 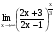 . . 2 1) 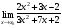 при а) при а) 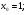 б) б) 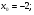 в) в) 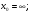 2) 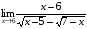 ; 3) ; 3) 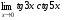 ; 4) ; 4) 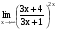 . . 3 1) 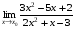 при а) при а)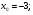 б) б)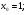 в) в) 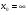 ; ;2) 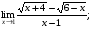 3) 3) 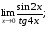 4) 4) 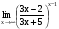 . .4 1) 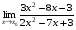 при а) при а) 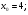 б) б) 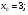 в) в) 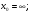 2) 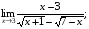 3) 3) 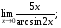 4) 4) 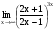 . .5 1) 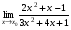 при а) при а) 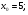 б) б) 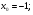 в) в) 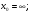 2) 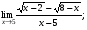 3) 3) 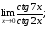 4) 4) 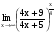 . .6 1) 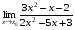 при а) при а) 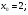 б) б) 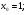 в) в)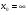 ; ;2) 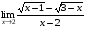 ; 3) ; 3) 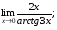 4) 4) 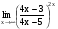 . .7 1) 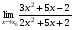 при а) при а) 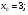 б) б) 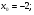 в) в) 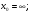 2) 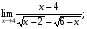 3) 3) 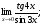 4) 4) 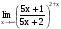 . .8 1) 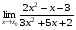 при а) при а) 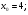 б) б) 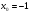 ; в) x0 = ∞; ; в) x0 = ∞;2) 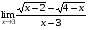 ; 3) ; 3) 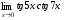 ; 4) ; 4) 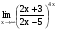 . .9 1) 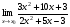 при а) при а)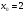 ; б) ; б) 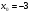 ; в) ; в) 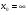 ; ;2) 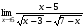 ; 3) ; 3) 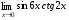 ; 4) ; 4) 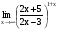 . .10 1) 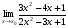 при a) при a) 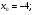 б) б) 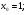 в) в)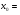 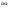 ; ;2) 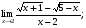 3) 3) 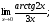 4) 4) 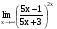 . .Серия В 1 1) 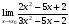 при а) при а) 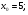 б) б) 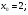 в) в) 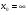 ; ;2) 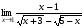 ; 3) ; 3) 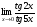 ; 4) ; 4) 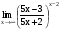 . .2 1) 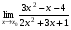 при а) при а) 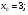 б) б) 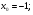 в) в)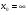 ; ;2) 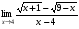 ; 3) ; 3) 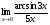 ; 4) ; 4) 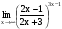 . .3 1) 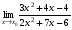 при а) при а) 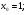 б) б) 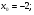 в) в) 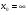 ; ;2) 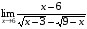 ; 3) ; 3) 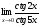 ; 4) ; 4) 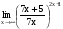 . .4 1) 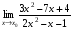 при а) при а) 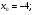 б) б) 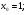 в) в) 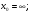 2) 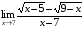 ; 3) ; 3) 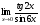 ; 4) ; 4) 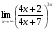 . .5 1) 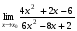 при а) при а) 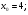 б) б) 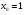 ; в) ; в) 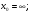 2) 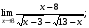 3) 3) 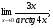 4) 4) 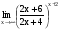 . .6 1) 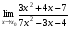 при а) при а) 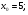 б) б) 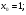 в) в) 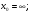 2) 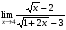 ; 3) ; 3) 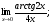 4) 4) 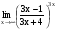 . .7 1) 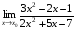 при а) при а)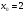 ; б) ; б) 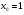 ; в) ; в) 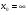 ; ;2) 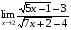 ; 3) ; 3) 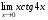 ; 4) ; 4) 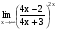 . .8 1) 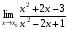 при а) при а)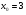 ; б) ; б) 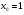 ; в) ; в) 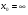 ; ;2) 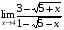 ; 3) ; 3)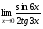 ; 4) ; 4) 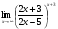 9 1)  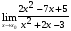 при а) при а) 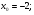 б) б) 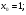 в) в) 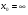 ; ;2)  3) 3) 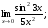 4) 4) 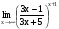 . .10 1) 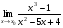 при а) при а) 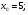 б) б) 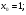 в) в) 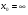 ; ;2) 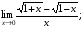 3) 3) 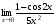 ; 4) ; 4) 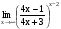 . .Задание 4. Найти интервалы непрерывности функции и точки разрыва. Построить график функции
Задание 5 Найдите производную 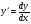 , пользуясь формулами дифференцирования. , пользуясь формулами дифференцирования. Серия А 1 a) 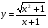 ; б) ; б) 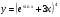 ; в) ; в) 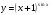 2 a) 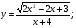 б) б) 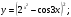 в) в) 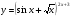 3 a) 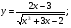 б) б) 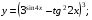 в) в) 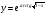 4 а) 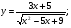 б) б) 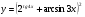 ; в) ; в) 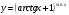 5 а) 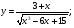 б) б) 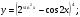 в) в) 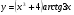 6 a) 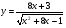 ; б) ; б) 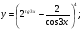 в) в) 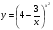 7 a) 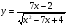 ; б) ; б) 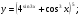 в) в) 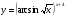 8 a) 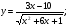 б) б) 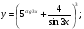 в) в) 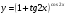 9 а) 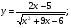 б) б) 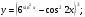 в) в) 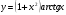 10 a) 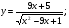 б) б) 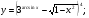 в) в) 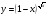 Серия В 1 а) 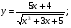 б) б) 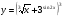 в) в) 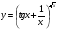 2 a) 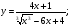 б) б) 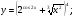 в) в) 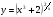 3 a) 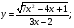 б) б)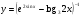 ; в) ; в) 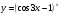 4 а) 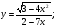 б) б) 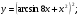 в) в) 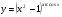 5 а) 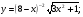 б) б) 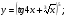 в) в) 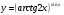 6 а) 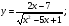 б) б) 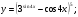 в) в) 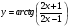 7 а) 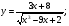 б) б) 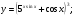 в) в) 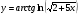 8 а) 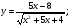 б) б) 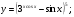 в) в) 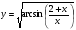 9 а) 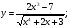 б) б) 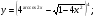 в) в) 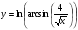 10 а) 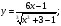 б) б) 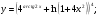 в) в) 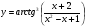 Задание 6 Найдите промежутки возрастания, убывания и точки экстремума функции 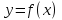 . .
Задание 7 Найдите неопределенные интегралы, результаты проверить дифференцированием. Серия А
Серия В
Задание 8 Найдите площадь фигуры, ограниченной линиями 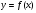 и и 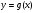 . .
Задание 9 Дана функция z=ƒ(x;y) Требуется: а) исследовать эту функцию на экстремум; б) найти условный экстремум при условии 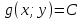 методом Лагранжа. методом Лагранжа.Серия А 1. 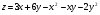 ; ; 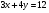 2. 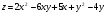 ; ; 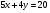 3. 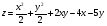 ; ; 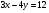 4. 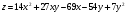 ; ; 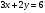 5. 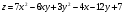 ; ; 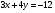 6. 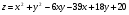 ; ; 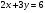 7. 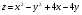 ; ; 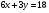 8. 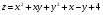 ; ; 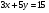 9. 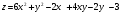 ; ; 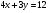 10. 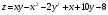 ; ; 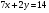 Серия В 1. 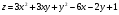 ; ; 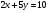 2. 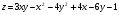 ; ; 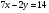 3. 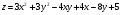 ; ; 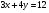 4. 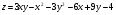 ; ; 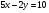 5. 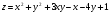 ; ; 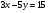 6. 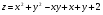 ; ; 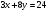 7. 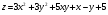 ; ; 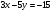 8. 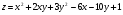 ; ; 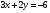 9. 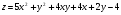 ; ; 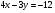 10. 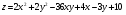 ; ; 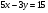 Задание 10 Серия А
Серия В
Задание 11 Найдите а) общее решение дифференциального уравнения первого порядка; б) частное решение дифференциального уравнения второго порядка при данных начальных условиях.
|

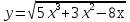
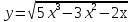
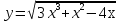
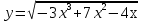
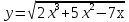
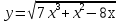
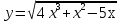
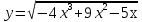
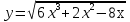
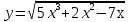
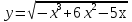
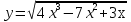
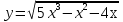
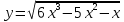
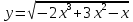
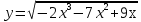
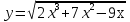
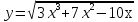
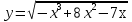
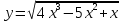
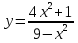
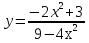
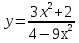
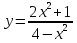
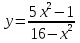
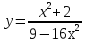
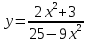
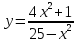
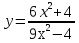
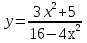
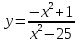
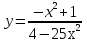
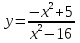
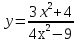
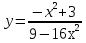
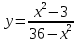
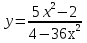
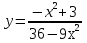
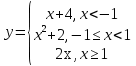
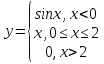
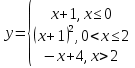
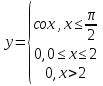
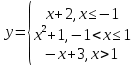
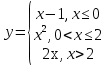
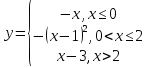
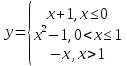
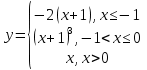
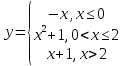
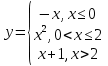
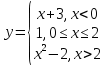
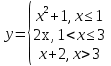
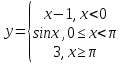
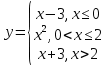
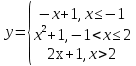
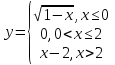
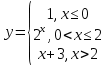
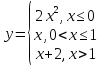
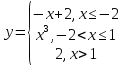
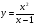
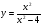
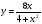
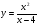
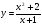
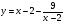
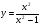
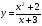
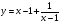
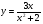
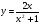
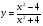
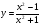
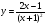
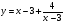
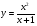
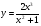
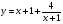
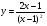
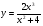
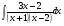 ; б)
; б)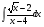 ; в)
; в)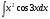
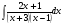 ; б)
; б)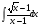 ; в)
; в)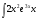
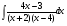 ; б)
; б)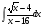 ; в)
; в)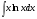
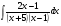 ; б)
; б)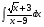 ; в)
; в)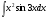
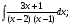
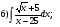 в)
в)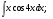
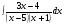 ; б)
; б)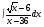 ; в)
; в)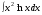
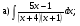
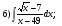
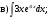
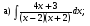
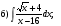
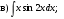
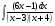 ; б)
; б)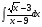 ; в)
; в)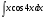
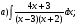
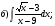
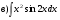
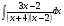 ; б)
; б) 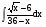 ; в)
; в)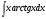
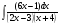 ; б)
; б)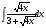 ; в)
; в) 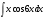
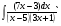 ; б)
; б)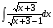 ; в)
; в) 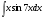
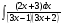 ; б)
; б) 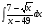 ; в)
; в) 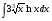
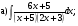
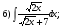 в)
в)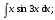
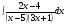 ; б)
; б) 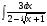 ; в)
; в) 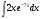
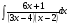 ; б)
; б) 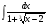 ; в)
; в)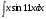
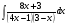 ; б)
; б) 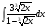 ; в)
; в)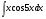
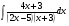 ; б)
; б)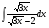 ; в)
; в)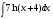
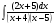 ; б)
; б) 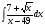 ; в)
; в) 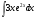
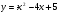
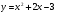
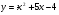
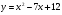
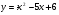
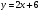
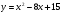
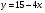
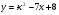
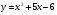
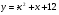
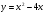
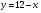
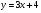
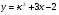
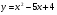
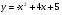
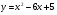
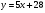
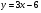
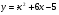
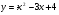
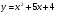
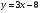
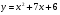
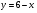
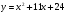
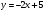
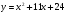
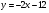
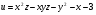 . Найти производную в точке
. Найти производную в точке 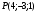 в направлении от этой точки к точке
в направлении от этой точки к точке 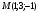 .
.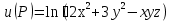 в точке
в точке 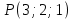 .
.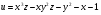 . Найти производную в точке
. Найти производную в точке 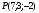 в направлении от этой точки к точке
в направлении от этой точки к точке 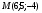 .
.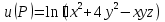 в точке
в точке 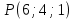 .
.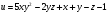 . Найти производную в точке
. Найти производную в точке 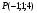 в направлении от этой точки к точке
в направлении от этой точки к точке 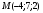 .
.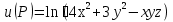 в точке
в точке 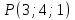 .
.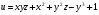 . Найти производную в точке
. Найти производную в точке 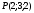 в направлении от этой точки к точке
в направлении от этой точки к точке 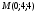 .
.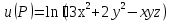 в точке
в точке 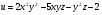 . Найти производную в точке
. Найти производную в точке 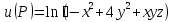 в точке
в точке 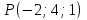 .
.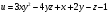 . Найти производную в точке
. Найти производную в точке 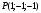 в направлении от этой точки к точке
в направлении от этой точки к точке 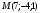 .
.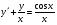 ;
; 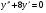 ; y(0)=1;
; y(0)=1; 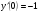
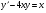 ;
; 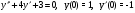
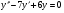 ; y(0)=1;
; y(0)=1; 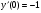
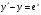 ;
; 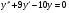 ; y(0)=1;
; y(0)=1; 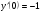
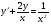 ;
; 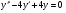 ; y(0)=1;
; y(0)=1; 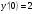
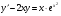 ;
; 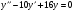 ; y(0)=0;
; y(0)=0; 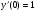
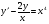 ;
; 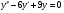 ; y(0)=1;
; y(0)=1; 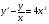 ;
; 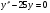 ;
; 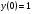 ;
; 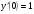
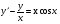 ;
; 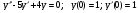
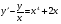 ;
; 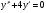 ; y
; y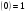 ;
; 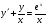 ;
; 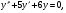 y(0)=1;
y(0)=1; 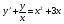 ;
; 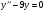 ; y(0)=-1;
; y(0)=-1; 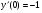
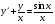 ;
; 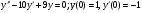
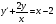 ;
; 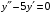 ;
; 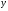 (0)=-1;
(0)=-1; 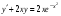 ;
; 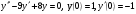
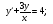
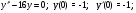
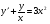 ;
; 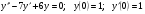
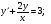
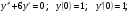
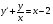 ;
; 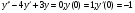
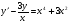 ;
;