Гидравлика_Вариант 2. Контрольная работа по предмету Гидравлика
 Скачать 328.25 Kb. Скачать 328.25 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ ИНСТИТУТ ТРАНСПОРТА Кафедра «Проектирование и эксплуатациянефтегазопроводов и хранилищ» Контрольная работа по предмету: «Гидравлика» Вариант 2 Выполнил:студент гр. Проверил: 2018 1 Задания по гидростатикеЗадание 1.1При гидравлическом испытании участка трубопровода с внутренним диаметром d и длиной l, проводимом с целью обеспечения безопасности технологических процессов и недопущения загрязнения окружающей среды, манометрическое давление жидкости было поднято до значения 55 ат. Пренебрегая деформацией трубопровода и изменением температуры, определить какой объём жидкости вытек из негерметичного трубопровода, если через один час давление в нём упало до 40 ат. Модуль упругости жидкости принять равным 2,0 109 Па. Исходные данные для задания 1.1:
Решение:Модуль объёмной упругости жидкости равен:  , ,где 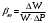 - коэффициент объёмного сжатия. - коэффициент объёмного сжатия.Отсюда получаем: 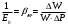 , , где 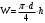 - первичный объём, - первичный объём,  -изменение объёма при изменении давления на величину -изменение объёма при изменении давления на величину  ( ( , ,  ). ).Следовательно, необходимое количество воды будет находиться по формуле: 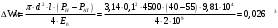 Давление в одну техническую атмосферу 1ат = 1кГ/см2 = 9,81 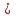 104 Па. 104 Па. Ответ:  Задание 1.2В вертикальной цилиндрической ёмкости диаметром D находится углеводородсодержащая жидкость, масса которой составляет m тонн, температура жидкости равна tоС, плотность = 870 кг/м3. Определить на какую величину изменится уровень углеводородсодержащей жидкости в ёмкости и минимальную допустимую высоту этой ёмкости с целью недопущения перелива жидкости через верх, приводящего к загрязнению окружающей среды, если температура её изменится от 0 оС до 35 оС. Расширением стенок ёмкости пренебречь. Коэффициент температурного расширения жидкости принять равным t= 0,00075 1/ оС. Исходные данные для задания 1.2:
Решение:Объем, занимаемый нефтью при t = 0 оC:  м3. м3.Изменение объема при повышении температуры на 35 оС:  м3. м3.Тогда, повышение нефти в резервуаре: 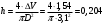 м. м.Уровень углеводородсодержащей жидкости в ёмкости при t = 0 оC:  м. м.Минимальная допустимая высота ёмкости с целью недопущения перелива жидкости через верх, приводящего к загрязнению окружающей среды, если температура её изменится от 0 оС до 35 оС: 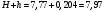 м или 8,0 м. м или 8,0 м.Задание 1.3Определить удельный вес жидкости, не смешивающейся с водой и находящейся в левом колене U - образной стеклянной трубки на высоте h над границей раздела жидкости и воды. Вода налита в правую часть трубки. Разность уровней жидкости и воды в коленах трубки Δh . Плотность воды принять = 1000 кг/м3. Исходные данные для задания 1.3:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| № варианта | Параметр | |
| d, м | p, ат | |
| 2 | 0,10 | 49 |
Решение:
Суммарная сила давления, разрывающая трубу в продольном направлении, равна гидростатическому давлению, умноженному на площадь вертикальной проекции криволинейной стенки:
 .
.Разрыв происходит по двум продольным сечениям стенки трубы. Напряжение, возникающее в материале стенки, равно
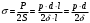 .
.Отсюда, минимальная толщина стенки трубопровода
 м = 3 мм.
м = 3 мм.
Ответ: минимальная толщина стенки трубопровода
 м = 3 мм.
м = 3 мм.Задание 1.5
Для экстренной защиты от аварийно разливающихся жидких углеводородов используют быстровозводимые защитные ограждения различных конструкций. Определить силу гидростатического давления жидких углеводородов на единицу длины заграждения, если в поперечном сечении оно имеют форму равнобедренного треугольника, а также определить точку приложения силы (центр давления), если высота столба жидкости перед заграждением h м, а угол при основании равнобедренного треугольника составляет градусов. Плотность жидких углеводородов у = 800 кг/м3.
Исходные данные для задания 1.4:
| № варианта | Параметр | |
| h, м | , град. | |
| 2 | 0,2 | 45 |
Решение:
1. Находим силу гидростатического давления:

где Р – сила гидростатического давления, Н
ω – площадь свободной поверхности, м2
ро – атмосферное давление, [ро=105 кг/м2]
hц – глубина погружения центра тяжести смоченной части площади поверхности, м
γ – удельный вес жидкости, [γ = ρ · g Н/м2],

h
h = 0,2 м
b = 0,4 м



450
b
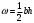 - поперечном сечении (площадь треугольника).
- поперечном сечении (площадь треугольника).Находим силу гидростатического давления на стенку в резервуаре А
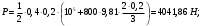
Сила избыточного гидростатического давления при р0 = ра
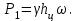

Эта сила приложена в центре давления, координата которой определяется по формуле

Ответ:
 .
.Задание 1.6
Основание понтона, представляет собой цилиндр с положительной плавучестью. Определить объём надводной части цилиндра незагруженного понтона, не единице его длины, если диаметр поперечного сечения цилиндра составляет d м, плотность материала, из которого он изготовлен, равна , а плотность воды в = 1000 кг/м3.
Исходные данные для задания 1.5:
| № варианта | Параметр | |
| d, м | , кг/м3 | |
| 2 | 0,21 | 510 |
Решение:
Общий вес понтона
 ,
,где
 - объём подводной части понтона;
- объём подводной части понтона; - плотность материала, из которого изготовлен понтон.
- плотность материала, из которого изготовлен понтон.Сила вытеснения (подъёмная сила) по закону Архимеда
 ,
,где
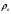 - плотность воды.
- плотность воды.При плавании соблюдается условие
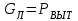 ;
; ,
,отсюда
 ,
, .
. , тогда,
, тогда,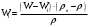 , отсюда,
, отсюда,
где
 ;
; .
.Подставляя цифровые значения в формулу, получим:
 .
.Ответ:
 .
.2 Задания по гидродинамике
Задание 2.1
По напорному трубопроводу диаметром d м перекачивается мазут, имеющий кинематическую вязкость = 1,5 Ст (стокс). Расход мазута составляет Q л/с. Определить режим движения жидкости.
Исходные данные для задания 2.1:
| № варианта | Параметр | |
| d, м | Q, л/с | |
| 2 | 0,10 | 20 |
Решение:
Чтобы определить режим движения мазута в трубопроводе, определим число Рейнольдса для данного диаметра труб и скорости потока:
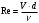 .
.Скорость потока равна:
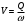 ,
, где
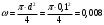 м2;
м2;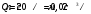 (1л = 1дм).
(1л = 1дм).Тогда,
 м/с.
м/с. = 1,5 Ст = 1,5· 10-4 м2/с (1 Ст = 1 см2/с)
 - режим ламинарный.
- режим ламинарный.
Задание 2.2
Определить режим движения воды в канале трапецеидального сечения. Ширина канала по дну составляет b м, глубина воды в канале h м, коэффициент заложения откосов боковых стенок m = 1,6. Расход воды в канале равен Q. Коэффициент кинематической вязкости воды в канале в равен 0,8 сСт (сантистокс).
Исходные данные для задания 2.2:
| № варианта | Параметр | ||
| b, м | h, м | Q, м3/с | |
| 2 | 2,2 | 2,2 | 4,1 |
Решение:
Число Рейнольдса для безнапорного движения определяют по формуле
Re = (Rυ) /ν,
где υ – средняя скорость движения жидкости, м/с;
ν – кинематический коэффициент вязкости, м2/с;
R – гидравлический радиус, м,
который может быть в общем случае найден по выражению:
R = ω /χ ,
где ω – площадь живого сечения потока, м2;
χ – смоченный периметр, м.
Критическое число Reкр. = 580.
Среднюю скорость движения воды находим по формуле :
 м/с.
м/с.Площадь живого сечения потока
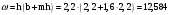 м2.
м2.Длина смоченного периметра :
χ=
 м.
м.Гидравлический радиус
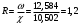 м.
м.
Число Рейнольдса для безнапорного движения:
 - режим турбулентный.
- режим турбулентный.в = 0,8 сСт = 0,8·10-6 м2/с.
Задание 2.3
Определить расход жидкости, пропускаемый самотечным напорным трубопроводом диаметром d и длиной l , если динамический коэффициент вязкости этой жидкости равен , её плотность равна , а разность отметок начальной и конечной точек трубопровода H составляет 2 м. Эквивалентная шероховатость стенок трубопровода э= 0,15 мм.
Исходные данные для задания 2.3:
| № варианта | Параметр | |||
| d, м | l, м | , Пас | , кг/м3 | |
| 2 | 0,10 | 41 | 0,002 | 999 |
Решение:
Выберем сечение 1–1 по свободной поверхности жидкости в резервуаре А, сечение 2–2 – по свободной поверхности жидкости в резервуаре В (рис. 1). Плоскость сравнения совместим с сечением 2–2.

Рисунок 1 – Схема к расчету расхода жидкости самотечного трубопровода
Составим уравнение Бернулли для сечений 1-1 и 2-2:

В данном случае:

Так как уровни в резервуарах А и В постоянны, то скоростные напоры
 и
и  равны нулю.
равны нулю.Подставив все значения в уравнение Бернулли, получим:

Откуда,
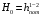 .
.Потери напора:

Область критических значений Re лежит обычно между 1500—2500. Зададим режим движения жидкости в трубопроводе турбулентный. Число Рейнольдса:
 .
.Определим расход
 .
.Отсюда,
 .
.Кинематическую вязкость определяют как отношение динамической вязкости к плотности вещества:
 .
.Расход жидкости , пропускаемый самотечным напорным трубопроводом, можно определить по формуле:
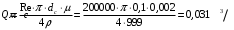
Средняя скорость жидкости в самотечном трубопроводе:
 м/с.
м/с.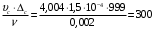
При
 , коэффициент потерь
, коэффициент потерь  на трение по длине определяем по формуле Альтшуля:
на трение по длине определяем по формуле Альтшуля:
где:
 – шероховатость чугунных (бывших в употреблении) труб.
– шероховатость чугунных (бывших в употреблении) труб.Вычислим величину потребного напора для пропуска расхода
 при значении диаметра самотечного трубопровода
при значении диаметра самотечного трубопровода  по формуле:
по формуле: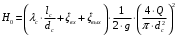

Ответ: расход жидкости, пропускаемый самотечным напорным трубопроводом, равен

Задание 2.4
Определить потери напора и давления по длине в новом стальном трубопроводе (эквивалентная шероховатость его стенок Э= 0,15 мм) диаметром d и длиной l , если по нему транспортируется вода с расходом Q = 400 л/с. Кинематическая вязкость воды в = 1 сСт, а её плотность = 1000 кг/м3. Как изменятся потери напора и потери давления, если по нему будет транспортироваться нефть с тем же расходом? Коэффициент кинематической вязкости нефти н принять равным 1 Ст, а плотность н = 850 кг/м3.
Исходные данные для задания 2.4:
| № варианта | Параметр | |
| d, м | l, м | |
| 2 | 0,50 | 1500 |
Решение:
Потери напора на трение по длине вычисляются по формуле Дарси-Вейсбаха
 ,
,где l- расстояние между рассматриваемыми сечениями, т.е. длина трубы,
 - скорость течения,
- скорость течения, d- внутренний диаметр трубы,
 - коэффициент гидравлических потерь на трение по длине,
- коэффициент гидравлических потерь на трение по длине,  - относительная шероховатость.
- относительная шероховатость.При течении жидкости в круглых трубах за характерный размер l объёма принимается внутренний диаметр трубы D, тогда число Рейнольдса:
 .
.Скорость течения:
 м/с.
м/с.Число Рейнольдса:
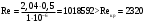 - режим турбулентный.
- режим турбулентный.в = 1 сСт = = 1·10-6 м2/с.
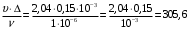
При
 , коэффициент потерь
, коэффициент потерь  на трение по длине определяем по формуле Альтшуля:
на трение по длине определяем по формуле Альтшуля: .
.Потери напора на трение по длине
 м.
м.Потери напора и давления связаны зависимостью.
Δp=Δhρg,
где ρ - плотность, g - ускорение свободного падения.
Потери давления по длине можно вычислить используя формулу Дарси — Вейсбаха:
 Па =48,4 кПа.
Па =48,4 кПа.Ответ:
 м,
м,  Па =94,8 кПа.
Па =94,8 кПа.Как изменятся потери напора и потери давления, если по нему будет транспортироваться нефть с тем же расходом? Коэффициент кинематической вязкости нефти н принять равным 1 Ст, а плотность н = 850 кг/м3.

При
 , коэффициент потерь
, коэффициент потерь  на трение по длине определяем по формуле Формула Блазиуса:
на трение по длине определяем по формуле Формула Блазиуса: .
.Потери напора на трение по длине
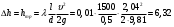 м.
м.Потери давления по длине:
 Па =52,7 кПа.
Па =52,7 кПа.Вывод: потери напора и потери давления уменьшатся.
Задание 2.5
В стальном трубопроводе длиной l , диаметром d , с толщиной стенок равной 6 мм, средняя по сечению скорость воды V = 1,7 м/с. Определить наименьшее время закрывания запорной арматуры tз, обеспечивающее повышение вызванного гидравлическим ударом давления в конце трубопровода не более 2,5 ат., не приводящего к разрыву трубопровода и нанесению ущерба окружающей среде. Как повысится давление в случае мгновенного перекрытия сечения трубопровода? Модуль упругости воды Eв = 2109 Па, модуль упругости стали Eс = 21011 Па , плотность воды в = 1000 кг/м3. Определить потери напора на задвижке при движении жидкости с заданной скоростью V, если коэффициент местного сопротивления будет равен 0,37.
Исходные данные для задания 2.5:
| № варианта | Параметр | |
| d, м | l, м | |
| 2 | 0,10 | 1100 |
Решение:
Явление повышения давления в трубопроводе при быстром закрывании задвижки называют гидравлическим ударом. Гидравлический удар обусловлен переходом кинетической энергии движущегося потока в потенциальную энергию давления при его остановке. Различают прямой и непрямой гидравлические удары.
Повышение давления определяют по формулам при прямом ударе ΔР=ρvc, при непрямом ударе

где ρ – плотность жидкости ( принять ρ = 1000 кг/м3);
v – средняя скорость движения;
c - скорость распространения ударной волны;
Т – фаза ударной волны;
Тз – время закрывания задвижки.
Тогда,
 .
.Величину Т определяют по формуле
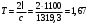 с.
с.Для случая движения воды в стальном трубопроводе

 с.
с.Если Тз <Т, то имеет место прямой гидравлический удар, если Тз >Т – непрямой гидравлический удар.
Определив величину Т и сопоставив ее с заданной величиной Тз, следует, что вид гидравлического удара, непрямой.
Явление гидравлического удара открыл в 1897-1899 г. Н. Е. Жуковский. Увеличение давления при гидравлическом ударе определяется в соответствии с его теорией по формуле:
где Dp — увеличение давления в Н/м², ρ — плотность жидкости в кг/м³, v0 и v1 — средние скорости в трубопроводе до и после закрытия задвижки (запорного клапана) в м/с, с — скорость распространения ударной волны вдоль трубопровода.
Увеличение давления при гидравлическом ударе:
 Па = 2,2 МПа = 22,9 ат.
Па = 2,2 МПа = 22,9 ат.Потери напора при движении жидкости в местных сопротивлениях определяются по формуле Вейсбаха:
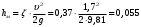 м,
м, где ζ — коэффициент местного сопротивления.
Ответ:
 с,
с,  Па = 2,2 МПа = 22,9 ат,
Па = 2,2 МПа = 22,9 ат, 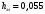 м.
м.Задание 2.6
Определить расход воды в канале трапецеидального сечения при равномерном движении жидкости в нём. Ширина канала по дну равна b, глубина воды в канале равна h, коэффициент заложения откосов m = 2. Продольный уклон дна i составляет 0,0014. Коэффициент шероховатости поверхности русла n = 0,018.
Исходные данные для задания 2.6:
| № варианта | Параметр | |
| b, м | h, м | |
| 2 | 9,8 | 2,9 |
Решение:
Расход Q при глубине воды в канале h определим по формуле Шези:
Вычисляем последовательно :
- площадь живого сечения потока
ω=h(b+mh)
 м2.
м2.- длину смоченного периметра русла :
χ=
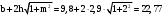 м.
м. - гидравлический радиус :
R=
 м.
м.- коэффициент Шези :
C=
 м/с.
м/с.- расходную характеристику :
K=
 м3/с.
м3/с.- расход :
Q =
 м3/с.
м3/с.Ответ: расход воды в канале трапецеидального сечения равен =
 м3/с.
м3/с.Задание 2.7
Определить время полного опорожнения вертикального цилиндрического резервуара с водой. Диаметр резервуара d. Начальная высота столба жидкости в резервуареH. Диаметр отверстия, расположенного в донной части резервуара d0 = 5см.
Исходные данные для задания 2.7:
| № варианта | Параметр | |
| d, м | H, м | |
| 2 | 9,8 | 2,9 |
Решение:
Опорожнение резервуара относится к неустановившемуся движению жидкости, так как параметры движения меняются во времени. В виду плавного изменения параметров движения его можно рассматривать, как квазиустановившееся движение и рассчитывать, используя метод смены стационарных состояний.
Время полного опорожнения определятся по формуле
 ,
,где Н - уровень жидкости в начальный времени;
 - площадь горизонтального сечения резервуара (площадь поверхности жидкости в резервуаре);
- площадь горизонтального сечения резервуара (площадь поверхности жидкости в резервуаре);  - площадь сечения отверстия.
- площадь сечения отверстия.При истечении жидкости через отверстие для маловязких жидкостей (вода, бензин, керосин) μ = 0,62.
Тогда,
 с = 13,2 ч.
с = 13,2 ч.Ответ: время полного опорожнения вертикального цилиндрического резервуара с водой
 с = 13,2 ч.
с = 13,2 ч.Задание 2.8
Определить время заполнения емкости водой, объем которой составляет W. Емкость заполняется из напорного бака, расположенного на высоте H. Вода поступает в емкость по трубопроводу диаметром d = 150 мм идлиной l=90м. На трубе имеются два вентиля с коэффициентом местного сопротивления ζв=12 у каждого, четыре прямых колена без закругления (ζк = 1,5). Режим движения воды в трубопроводе турбулентный в зоне гидравлически шероховатых труб. Коэффициент гидравлического трения λ = 0,02. Абсолютная эквивалентная шероховатость стенок трубопровода ∆э = 0,5 мм. Расходная характеристика, (модуль расхода) такого трубопровода К2 = 34103 л2/с2.
Исходные данные для задания 2.8:
| № варианта | Параметр | |
| W, м3 | H, м | |
| 2 | 29 | 29 |
Решение:
Запишем уравнение Бернулли для первого и второго сечений:
 . Поскольку
. Поскольку  , что течение жидкости турбулентное. Высоту будем отсчитывать от сечения 1-1. Так как сечение 2-2 совпадает с поверхностью жидкости то
, что течение жидкости турбулентное. Высоту будем отсчитывать от сечения 1-1. Так как сечение 2-2 совпадает с поверхностью жидкости то 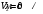 . Распишем потери на трубопроводе
. Распишем потери на трубопроводе  :
:  - потери на входе в трубу (
- потери на входе в трубу ( ), где
), где  - скорость жидкости в трубе;
- скорость жидкости в трубе;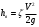 - потери на вентиле;
- потери на вентиле; - потери на выходе (
- потери на выходе (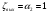 );
);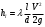 - потери по длине трубы.
- потери по длине трубы.  - коэффициент сопротивления трения, зависящий от числа Рейнольдса, диаметра трубы и шероховатости. В нашем случае
- коэффициент сопротивления трения, зависящий от числа Рейнольдса, диаметра трубы и шероховатости. В нашем случае  (
( ,
,  ).
).Найдем приведенную длину трубопровода: lпр = l+∑ lэкв .
Эквивалентная длина рассчитывается по формуле lэкв = ζ∙d/l ,
 м.
м.Тогда, приведенная длина трубопровода
 м.
м.Напор в сечении 1-1 тратится на преодоление линейных потерь hл.п, т.е. Н = hл.п.. тогда
 .
.Отсюда,
 м3/с.
м3/с.Время заполнения емкости водой, объем которой составляет W.
 с = 4,6 мин.
с = 4,6 мин.библиографический список
Богомолов А.И., Михайлов К.А. Гидравлика: учеб. для гидротехн. спец. вузов. - 2-е изд., перераб. и доп. – М.: Стройиздат, 1972. – 648 с.
Ильина Т.Н. Основы гидравлического расчета инженерных сетей : учеб. пособие / Е. Н. Ильина .— М. : АСВ, 2007 .— 192 с.
Крестин Е.А., Крестин И.Е. Задачник по гидравлике с примерами расчетов. Учеб. пособие. – 3-е изд., доп. –СПб.: Издательство «Лань», 2014. – 320 с.
Кудинов В.А., Карташов Э.М. Гидравлика: Учебное пособие мо. – 2-е изд., перераб. и доп. – М., 2007: Высшая школа.-199 с.
Примеры расчетов по гидравлике/ Под. ред. А.Д. Альтшуля. – М.: Стройиздат, 1977. – 256 с.
Справочник по гидравлическим расчетам/ Под ред. П.Г. Киселева. – изд. 5-е. – М.: «Энергия», 1974. – 312 с.
Чугаев Р.Р. Гидравлика: учебник/ Р.Р. Чугаев. – 5-е изд., репринт. – М.: БАСТЕТ, 2008. – 672 с.
Штеренлихт Д.В. Гидравлика: Учебник мо /Штеренлихт Д.В. – М : КолосС, 2004.- 656 с .


 и давления второй жидкости
и давления второй жидкости  , а давление справа второй жидкости равно
, а давление справа второй жидкости равно  . Приравнивая давления, получаем:
. Приравнивая давления, получаем: 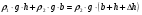 ,
,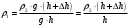 .
.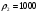 кг/м3 – плотность воды), получаем:
кг/м3 – плотность воды), получаем:  кг/м3.
кг/м3.  кг·м/(с2·м3) = 71873,3 Н/м3.
кг·м/(с2·м3) = 71873,3 Н/м3.