Теория анализа и статистики 37 вариант. теори анализа и статистики. Контрольная работа по теме Теория анализа и статистики
 Скачать 165.5 Kb. Скачать 165.5 Kb.
|
|
Минобрнауки России федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный технологический институт (технический университет)» ЗАДАНИЕ Контрольная работа по теме «Теория анализа и статистики» Вариант 37
Учебный модуль Теория анализа и статистики Курс 1 Группа 606зэ-6 Студент Ермакова Татьяна Евгеньевна (Ф.И.О.) Номер личного дела: 201932 Номер работы: 37 Цель работы _____________________________________________________ Исходные данные _________________________________________________ Дата выдачи задания _____________________________________
Задание 1 Монополия производит фиксированное количество x единиц товара и устанавливает цену единицы товара 𝑝>𝑝0. Количество реализованного товара K зависит от p следующим образом: Определить значение p, при котором монополия получит максимальную прибыль. Решение: Составим функцию прибыли при цене р: Найдем производную функции прибыли: Приравняем производную к нулю: Производная равна нулю при р = 1, при переходе через точку р = 1 производная меняет знак с плюса на минус, следовательно, в точке р = 1 функция прибыли имеет максимум. Ответ: р = 1 Задание 2 Дана матрица прямых затрат: Найти: а) вектор валовой продукции Х для обеспечения выпуска конечной продукции Решение: Коэффициенты матрицы Столбец Найдем матрицу материальных затрат коэффициентов полных В – матрица коэффициентов полных материальных затрат (обратная матрица Леонтьева). Элемент bij показывает, каким должен быть валовой выпуск i-ой отрасли для того, чтобы обеспечить производство единицы конечного продукта j-ой отрасли. Е – единичная матрица. Вводим единичную матрицу Е второго порядка и находим разность матриц: Находим определитель, полученной матрицы: Т.к. определитель матрицы не равен нулю, значит, действительно существует обратная матрица. Находим обратную матрицу: Т.к. существует обратная матрица и все ее элементы не отрицательны, значит матрица А продуктивна. Найдем объем валовой продукции каждой отрасли Х – величина валового производства отраслей. Вектор-столбец Вектор строка Определим приращение вектора ∆Х для увеличения выпуска конечной продукции на Ответ: Вектор валовой продукции Задание 3 Производственная функция В силу бюджетных ограничений на ресурсы может быть потрачено не более 600 (ден. ед.). В этих условиях найти оптимальное для производителя значение (𝑥,𝑦) количества используемых ресурсов. Решение: Производственная функция в денежном выражении равна доходу от использования ресурсов. Функция затрат на ресурсы: Таким образом, функция прибыли равна: Требуется найти значения величин используемых ресурсов (х, у), при которых фирма-производитель получит максимальную прибыль при ограничении: Запишем ограничение как равенство: В силу ограничений имеем Тогда функция прибыли: Находим производную функции прибыли: Приравниваем ее к нулю Получим, у = 24, откуда х = 120 – 2×24 = 72 Максимальная прибыль при этом равна 30×72×24 – 5×72 – 10×24 = 51 240 (ден.ед.) Ответ: Максимальная прибыль составит 51 240 ден.ед. при х = 72, у = 24. Задание 4 Найти объем выпускаемой продукции за пять лет, если в функции Кобба–Дугласа Решение: Пусть функция 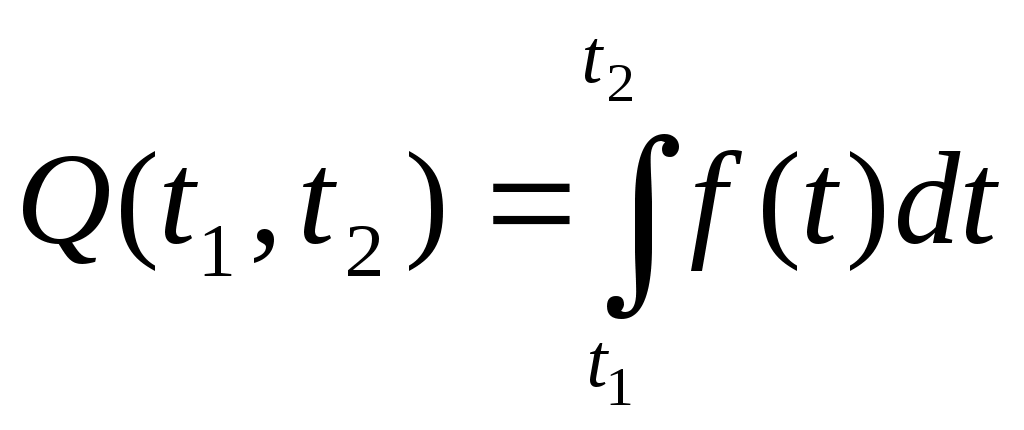 Подставляя функцию производительности в формулу. получаем: Применяя дважды последовательно формулу интегрирования по частям Ответ: Объем выпускаемой продукции за 5 лет составит 64825. Задание 5 Случайная величина Х имеет показательное распределение с параметром Решение: Для непрерывной случайной величины, распределенной по показательному закону плотность распределения следующим образом: 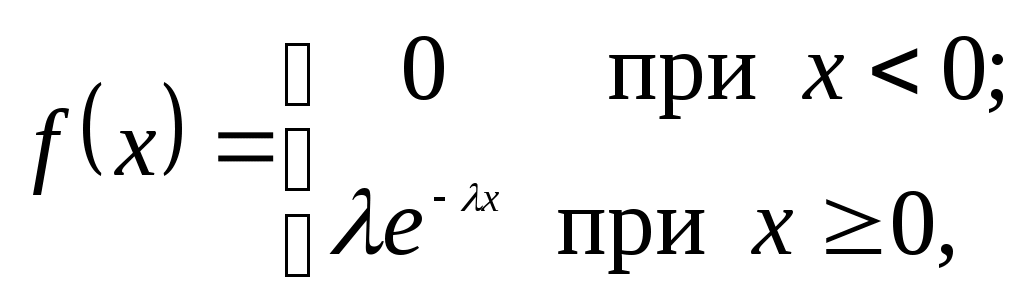 , где , гдеПри 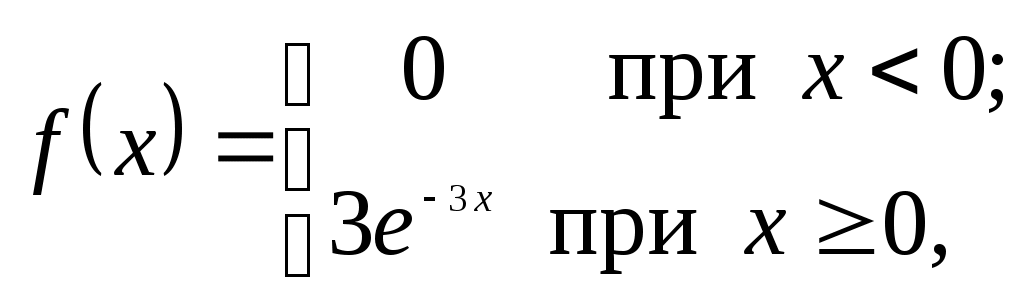 Функция распределения показательного закона: 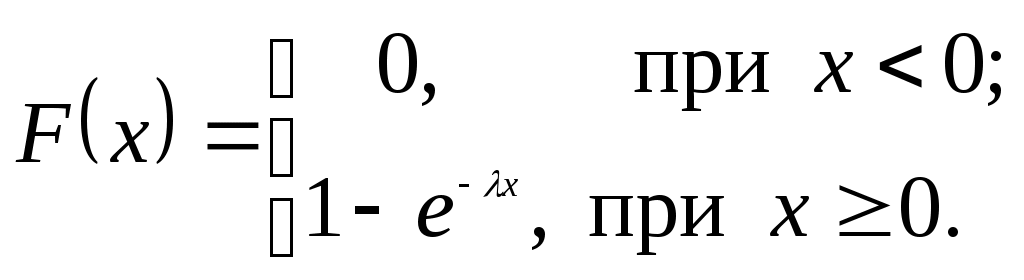 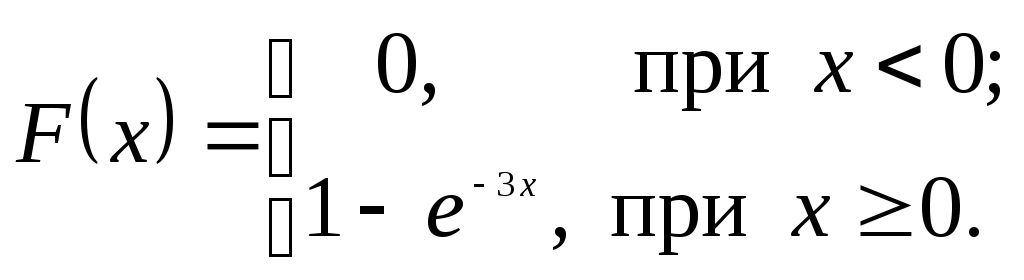 Т.к. при Математическое ожидание: 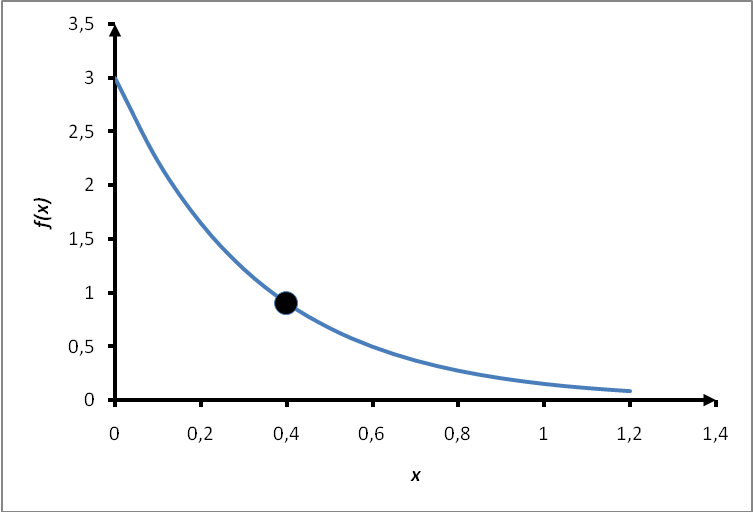 Рисунок 1 – График плотности распределения Ответ: Математическое ожидание |
